Simple interest and Compound interest are the Growth mechanisms
Simple interest for a year is the percentage rate of interest applied on the initial amount invested and it is fixed year to year. On the other hand, Compound interest is the percentage rate of interest applied on the amount available at the beginning of the year, and not at the beginning of the investment period.
Environment of Simple interest and Compound interest
The concepts of Simple interest and Compound interest mainly relate to the situation when an amount of money $A$ is invested at a rate interest of $r$% per annum (or suitable time period) for $n$ years (or $n$ number of periods).
The initial investment amount $A$ is called the Principal amount on which the interest rate is applied for the period of investment of $n$ periods. The unit of a period is usually a year but it may very well be six months or even one month.
This kind of investment generates or accrues an interest of amount $I$ at the end of $n$ number of periods. How much the interest $I$ will be after $n$ number of periods is determined by the type of interest in the form of investment under Simple interest or Compound interest. We will shortly explain the mechanism of these two usual forms of interest accrual.
There are two entities involved in an investment, the investor and the investment agency. The investor keeps the amount with the investment agency for the period of investment with an understanding (or agreement) that each year an interest of agreed percentage of the investment amount will be accumulated till the end of the period of investment. When the agreed period of investment is over, the investment agency will return the original amount plus the accumulated interest to the investor.
A common example of this mechanism in action is, when a customer like you and me, makes a fixed deposit of say, Rs.5 lakhs (1 lakh is 1 hundred thousand), at the interest of 7% compounded per annum for 3 years in a bank where the customer has an account. At the end of 3 years, if nothing greatly untoward happens, the customer gets back from the bank, Rs.5 lakhs of the original amount plus an interest of Rs.22504 accumulated over 3 years, a total of Rs.122504.
The interest is the gain of the customer because of the investment made in the bank in the form of a Fixed Deposit.
But why does a bank pays the customer the extra interest amount?
It gets investment funds from great many customers to build a large amount which is used as investment in running large projects or given as loan at a higher rate of interest to another set of customers. Bank is a financial institution and most of the projects in a country are run from financing by financial institutions like banks.
We will stop our environmental details at this point and go into the mechanisms of the clear cut precise topics of Simple interest and Compound interest.
Simple interest
When an amount of $A$ is invested at a simple interest rate of $r$% per year for $n$ years, each year the interest accrued will be same and fixed as,
$I_{year}=Ar$,
where $r$% is to be always applied to the principal amount $A$.
So at the end of $n$ years, the accumulated interest will be,
$I_n=nAr$.
For example, if $A=100$, $r=20$% per year and $n=6$ years, interest for each year will be fixed as,
$I_{year}=100\times{0.2}=\text{Rs.}20$.
So at the end of the 6th year the total accumulated interest will be,
$I_6=6\times{\text{Rs.}20}=\text{Rs.}120$.
The total amount at the end of 6 years will then be,
$A_6=A + I_6=100+120=\text{Rs.}220$.
The amount after each year of interest if plotted against number of years, it will generate a straight line, as the growth of the amount is linear like the following,

This is all there is to simple interest. Let us now get into compounding of interest.
Compound interest
Compound interest mechanism compounds the interest each year. Effectively the compound interest for a year is calculated with amount as in the beginning of the year, and not in the beginning of the period of investment. Thus each year as the amount increases by the interest of the previous year, when interest mechanism is applied on this amount it becomes,
$\text{Interest on the Principal amount}$ + $\text{Interest on the total interest accumulated till now}$.
If $A$ is the principal amount as before, $r$% is the percentage interest compounded on the amount each year, and $n$ is the number of years, amount at the end of the first year is,
$A_1=A+Ar=A(1+r)$.
In the second year the interest percentage is applied on this amount at the beginning of the second year so that at the end of the second year the amount becomes,
$A_2=A_1(1+r)=A(1+r)^2$.
Similarly the amount at the end of the $n$th year becomes,
$A_{n(compound)}=A(1+r)^n$.
Compare this amount with the amount when under simple interest mechanism,
$A_{n(simple)}=Arn$.
Because of the compounding of interest, or interest on interest generated each year, under compounding mechanism, the interest and hence the amount increases much faster compared to simple interest. The growth of amount in this case is thus not linear, it is a growth, rate of which increases with each passing year. The rate of growth in this case is not constant for each year as in case of simple interest.
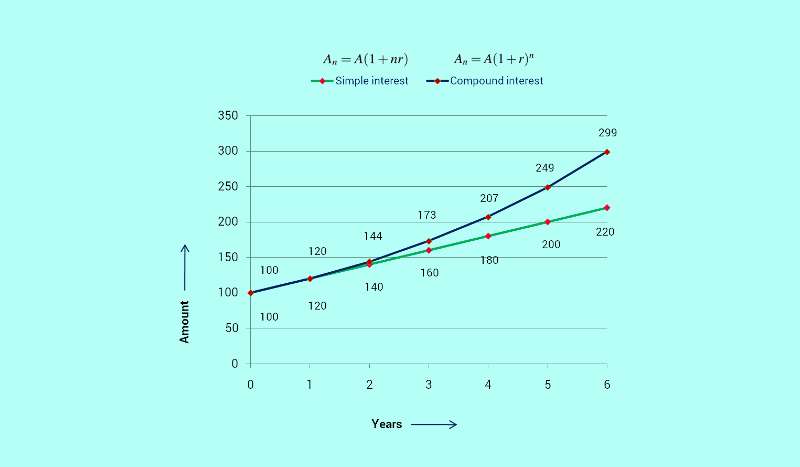
With principal amount, $A=\text{Rs.}100$, rate of interest, $r=20$% and period of investment, $n=6$ years, under simple interest scheme the amount at the end of 6th year will be,
$A_{6(Simple)}=A(1+rn)=100+6\times{100}\times{0.2}=\text{Rs.}220$.
On the other hand in case of compound interest scheme, with values of amount $A=100$, $r=20$% and $n=6$ years, at the end of 6th year the amount will approximately be,
$A_{6(Compound)}=A(1+r)^n=100(1+0.2)^6=\text{Rs.}299$.
The variations are pictorially shown below,

The most important point to remember is, the compound interest on the $n$th year will be,
$I_n=A_{n-1}r$,
where $A_{n-1}$ is the amount accumulated at the beginning of the nth year, that is, at the end of $(n-1)$st year, and $r$% is the compounding rate of interest.
In other words, in compound interest scheme,
To calculate the interest for a particular year, the interest percentage is applied on the amount available at the beginning of the year for which interest is being calculated.
These are the basic concepts on which rest of the concepts on simple interest and compound interest are built up.
Principal amount multiplying itself in a certain number of years - rich concept
Problem example 1.
If an amount is doubled when compounded at a particular rate of interest in 4 years then how many years will be taken to make the amount 4 times of itself at the same rate of compound interest?
- 6 years
- 8 years
- 5 years
- 7 years
Solution to problem example 1.
If the original amount $A$ is doubled to an amount of $A_4=2A$ in 4 years, instead of $A$, the amount $A_4$ would also have been doubled by the same interest rate in 4 years. In another 4 years then $A_4$ which is already $2A$ after the first 4 years will again be doubled, that is, the original amount $A$ will be 4 times of itself.
Just to remind you, in 4 years, any amount $A$ or $A_4$ will be doubled as stated. The problem statement indirectly specifies no restriction on the principal amount. But for an amount $A$ to become 4 times of itself, first it has to be doubled to $2A$ in 4 years and then starting from the 5th year, in another 4 years it will become double of $2A$, that is, four times of initial amount $A$. The total duration will then be 8 years
Answer: Option b: 8 years.
Note: In this solution we have used Mathematical reasoning which is based on concepts. This is the much faster way to the solution compared to using mathematical deduction.
Mathematical deduction to solution
$A_4=A(1+r)^4=2A$,
Or, $(1+r)^4=2$.
If $A$ becomes 4 times in $x$ years,
$A_x=4A=A(1+r)^x$,
Or, $4=(1+r)^x$,
Or, $2^2=(1+r)^x$
Or, $[(1+r)^4]^2=(1+r)^x$,
Or, $(1+r)^8=(1+r)^x$.
So the total number of years required for the initial amount to become 4 times of itself is 8 years.
It is a rather involved deduction.
The most basic concept at the core of compounding is, the interest rate calculation is on the amount at the beginning of each interest calculation year.
Loan repayment in two equal installments - rich concept
We will explain the concept through a second problem example.
Problem example 2.
Ramu borrowed Rs.2100 from Shyam at an annual compound interest rate of 10% with the understanding that in two equal installments each year Ramu will repay the loan completely. What was the installment amount?
- Rs.1210
- Rs.1220
- Rs.1225
- Rs.1226
Solution to problem example 2.
If Ramu were to return the borrowed or loaned money at the end of 2 years, he would have had to return back the principal of Rs.2100 plus the accumulated compound interest, that is, a total of,
$A_2=2100(1+0.1)^2=2100(1.21)=\text{Rs.}2541$.
Instead, as Ramu is repaying his first installment at the end of the first year, the amount on which interest would be calculated gets reduced by the installment amount.
The second year interest is calculated by applying the rate of interest 10% on this reduced amount. The interest added to the reduced amount at the beginning of the second year becomes the amount due at the end of second year. This is finally repaid by Ramu to wipe out the loan completely.
Thus in two installment repayments Ramu pays the loaned amount plus the compound interest duly accrued.
Obviously he would pay in total less that Rs.2541, because by first installment he reduces his outstanding loan and consequently his second year interest.
The first year end outstanding loan is,
$A_1=2100+0.1\times{2100}=2310$.
If $x$ be the installment, the outstanding loan at the beginning of second year reduces to,
$A_{1n}=2310-x$.
The second year end outstanding loan is thus,
$A_{2n}=(2310-x)+0.1(2310-x)=x$, as per loan repayment requirement.
So,
$2.1x=2541$,
Or, $x=1210$.
Let us check this value of installment to get a feel of the mechanism of installment.
At the end of first year when Ramu repays the first installment, the amount due reduces to,
$\text{Rs.}(2310-1210)=\text{Rs.}1100$.
During the second year an interest of,
$\text{Rs.}1100\times{0.1}=\text{Rs.}110$
is added to Rs.1100, the starting amount, making the dues as, Rs.1210, exactly the installment amount repaid at the end of the first year by Ramu.
This second year end due amount equal to the first year end installment is then paid off by Ramu as the second installment to wipe off the loan and interest dues completely.
Answer: Option a: Rs.1210.
Note: To take into account the effect of reducing the outstanding liability midway between the total loan period, this method couldn't use the whole period interest formula. Instead it has broken up the interest accrual process year to year based on the most fundamental interest compounding mechanism over a single period of loan or investment. This is Time breakdown technique.
Exercise
As exercise you need to solve the 10 selected problems in SSC CGL level Question Set 50 on Simple interest and Compound interest within the prescribed time limit. At the end of the question set you will find the answers.
For detailed solution to this question set, you should refer to the paired SSC CGL level Solution Set 50 on Simple interest and Compound interest, but not before you have actually done the 10 problem exercise.
More related Question and solution sets on simple and compound interest
SSC CGL level Solved Questions Set 79 on Simple and Compound Interest 2