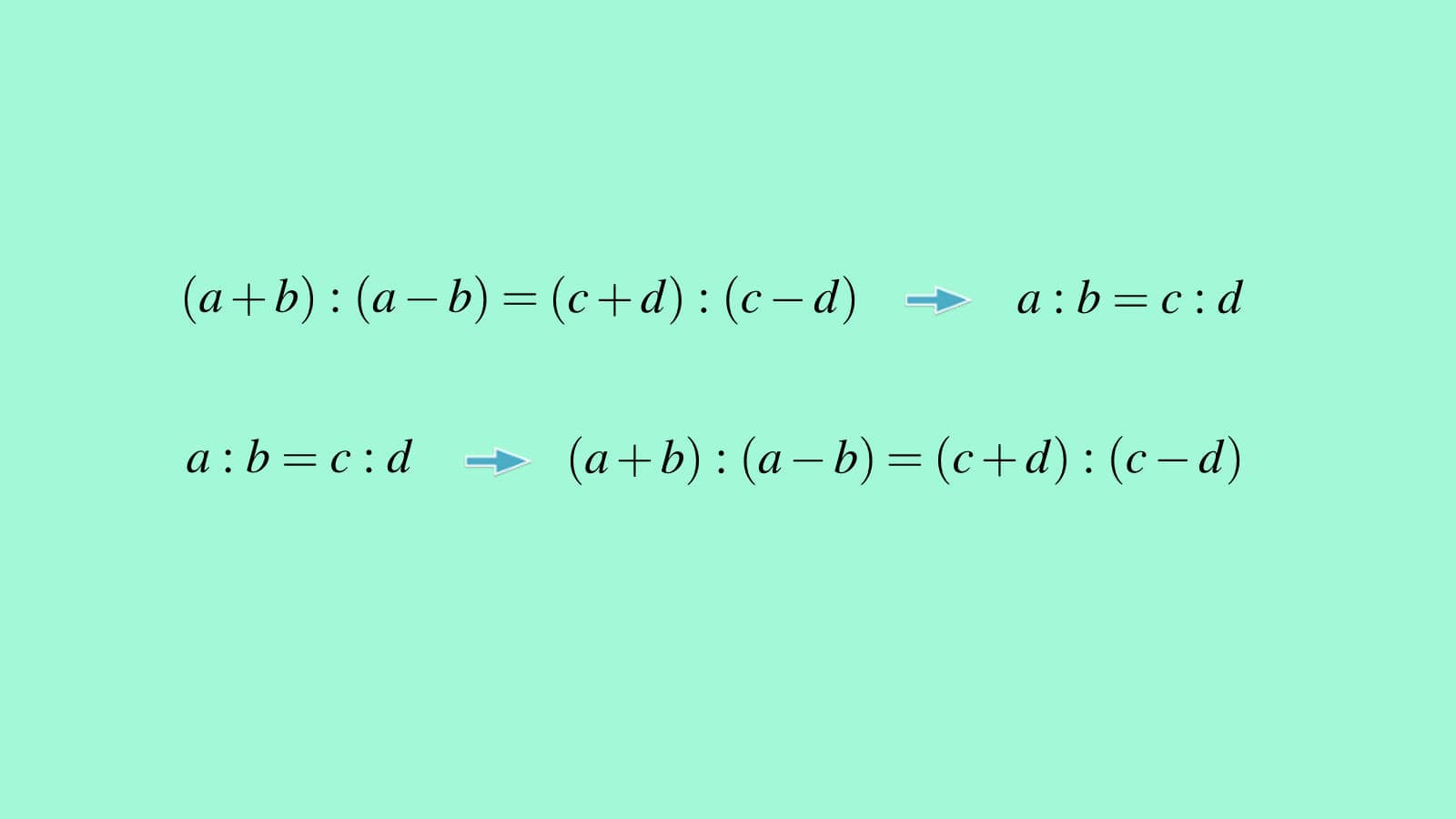
Componendo dividendo rule simplifies problems on many math topics lightning quick
You'll know what is Componendo dividendo, the proportion based simplification method, and how best to use the method to answer difficult questions quickly.
Sections are,
- Characteristics of Componendo dividendo.
- First basic form of application of Componendo dividendo and its proof: What is Componendo and what is Dividendo.
- Second basic form of application of Componendo dividendo and its proof.
- Third basic form of application of Componendo dividendo and its proof.
- Problem example 1 on Componendo dividendo and its solution: Given proportion in the form of a linear equation.
- Problem example 2 on Componendo dividendo and its solution: Coefficients of given proportion ratio term variables unequal.
- How would you know that Componendo dividendo is to be applied: Signature of Componendo dividendo.
- Problem example 3 on Componendo dividendo and its solution: Componendo dividendo in trigonometry.
Characteristics of Componendo dividendo
- Componendo dividendo is a proportion based 3 step quick method of simplifying the relation between the quantities in a given proportion (like $a:b=c:d$, where ratio $a:b$ is proportional to the second ratio $c:d$ with constant of proportion 1).
- It minimizes the steps otherwise needed.
- Because of its simplicity, the method can always be carried out mentally just like a formula or a rule. That's why often it is called in the name of Componendo dividendo rule or Componendo dividendo formula.
Usually Componendo dividendo is applied in three basic forms, though it can also be adapted and modified in different ways. But that will come later. For now we'll start with the basics.
First basic form of application of Componendo dividendo
Given the proportion $a:b=c:d$, by applying Componendo dividendo on the proportion it follows,
$(a+b):(a-b)=(c+d)(c-d)$.
Proof of Componendo dividendo rule in its first basic form
Given,
$\displaystyle\frac{a}{b}=\frac{c}{d}$$\qquad \qquad \qquad \qquad$ $\text{.................Proportion}$
Step 1: Componendo: Add 1 to both sides of the proportion equation,
$\displaystyle\frac{a+b}{b}=\frac{c+d}{d}$$\qquad \qquad$ $\text{...................1, Componendo}$
Step 2: Dividendo: Subtract 1 from both sides of the proportion equation,
$\displaystyle\frac{a-b}{b}=\frac{c-d}{d}$ $\qquad \qquad$ $\text{...................2, Dividendo}$
Step 3: Take the ratio of the two equations (divide equation 1 by equation 2) combining Componendo and Dividendo,
$\displaystyle\frac{a+b}{a-b}=\frac{c+d}{c-d}$ $\qquad \qquad \qquad \text{.............3, Componendo and Dividendo}$.
Being inherently simple and specific, instead of actually doing the 3 step operations, the final result can be obtained directly like using a formula or a rule, the Componendo dividendo rule.
You may be wondering,
Instead of simplifying the relation between the quantities in the ratio, it is made more complex!
You are right on this first basic form. But remember,
- Componendo dividendo can be applied in many forms as needed.
- Just as in the first form where Componendo dividendo is applied on proportion $a:b=c:d$, it can also be applied on the given proportion as, $(a+b):(a-b)=(c+d)(c-d)$ with the result, $a:b=c:d$. This is reverse of the first simple form.
Second basic form of application of Componendo dividendo
Given, $(a+b):(a-b)=(c+d)(c-d)$, by Componendo dividendo it follows,
$a:b=c:d$.
Proof of Componendo dividendo rule in its second basic form
Given,
$(a+b):(a-b)=(c+d)(c-d)$,
Or, $\displaystyle\frac{a+b}{a-b}=\frac{c+d}{c-d}$.
Step 1: Add 1 to both sides of the given proportion,
$\displaystyle\frac{2a}{a-b}=\frac{2c}{c-d}$ $\qquad \qquad$ $\text{...................4, Componendo}$,
Step 2: Subtract 1 from both sides of the proportion,
$\displaystyle\frac{2b}{a-b}=\frac{2d}{c-d}$ $\qquad \qquad$ $\text{...................5, Dividendo}$.
Step 3: Divide equation 4 by equation 5,
$a:b=c:d$, $\qquad \qquad \qquad \text{...................6, Componendo Dividendo}$.
Let us see how to use the Componendo Dividendo rule for a third form of given proportion.
Third basic form of application of Componendo dividendo
Given, $(a-b):(a+b)=(c-d)(c+d)$, it follows $a:b=c:d$.
Two numerators have subtraction instead of addition.
Proof of Componendo dividendo rule in its third basic form
Given,
$(a-b):(a+b)=(c-d)(c+d)$,
Or, $\displaystyle\frac{a-b}{a+b}=\frac{c-d}{c+d}$.
Step 1: Add 1 to both sides of the given proportion,
$\displaystyle\frac{2a}{a+b}=\frac{2c}{c+d}$ $\qquad \qquad$ $\text{...................7, Componendo}$.
Step 2: Subtract 1 from both sides of the proportion,
$\displaystyle\frac{-2b}{a+b}=\frac{-2d}{c+d}$ $\qquad \qquad$ $\text{...................8, Dividendo}$.
Step 3: Divide Equation 3 by Equation 4 eliminating the negative sign on both sides of the equation,
$a:b=c:d$, $\qquad \qquad$ $\text{...................9, Componendo dividendo}$.
These are three of the most basic forms for applying Componendo dividendo.
Remember
To operate on Proportions expressed in the form of $a:b::c:d$, you have to first convert the proportion to an equation of fractions.
Let us solve a few actual problems to consolidate how Componendo dividendo is applied in various types of problems.
Problem example 1 on Componendo dividendo: The given proportion in the form of a linear equation
If $2a-3b=0$ find the value of $(a- b):(a+b)$.
Solution to problem example 1.
Before applying Componendo dividendo on it, you have to convert the given equation to the proportion equation form,
$a:b=3:2$,
Or, $\displaystyle\frac{a}{b}=\frac{3}{2}$.
Add 1 to both sides of the equation,
$\displaystyle\frac{a+b}{b}=\frac{3+2}{2}=\frac{5}{2}$.
Subtract 1 from both sides of the equation,
$\displaystyle\frac{a-b}{b}=\frac{3-2}{2}=\frac{1}{2}$.
Dividing second equation by the first (dividing result of dividendo by that of componendo),
$\displaystyle\frac{a-b}{a+b}=\frac{1}{5}$.
Answer: $\displaystyle\frac{1}{5}$.
In this case you have modified the usual 3 step operation of Componendo dividendo in the third step.
Instead of dividing result of Componendo by that of dividendo, you have done the reverse, and that was the need for getting the solution correctly.
Caution
The method of Componendo dividendo looks simple, and actually it is simple.
But like all simple methods that can be applied on a wide variety of problems, you may have to MODIFY THE 3 STEP OPERATIONS suitably so that you get the desired target relation without any error.
Exercise for you
If $3a-2b=0$ find the value of $(7b-5a):(7b+5a)$.
Hint: Find first the value of $\displaystyle\frac{7b}{5a}$ from the given equation.
These are the two terms that are same between numerator and denominator of the desired ratio. Only difference is in their sign. So Componendo dividendo can be directly applied on $\displaystyle\frac{7b}{5a}$.
Problem example 2 on Componendo dividendo: Coefficients of given proportion ratio term variables unequal
If $\displaystyle\frac{2a-3b}{2a+3b}=\frac{1}{2}$, what is the value of $\displaystyle\frac{3b}{2a}$?
Solution to problem example 2
In the desired ratio the numerator being $3b$, it has to be in the numerator of one of the first two operations before combining componendo with dividendo.
In first step of Componendo, add 1 to both sides of the given proportion creating $2a$ in the numerator of the result,
$\displaystyle\frac{4a}{2a+3b}=\frac{3}{2}$, the factor 2 of $2\times{2a}$ will cancel out in third step.
In the second step of dividendo we must create $3b$ in the numerator.
Instead of the normal form of dividendo, modify the process by SUBTRACTING BOTH SIDES OF THE EQUATION FROM 1,
$\displaystyle\frac{6b}{2a+3b}=\frac{1}{2}$.
Again modify the process of dividing result of componendo by that of dividendo.
Instead, divide the result of dividendo by that of componendo, that is, divide the second resultant equation by the first,
$\displaystyle\frac{3b}{2a}=\frac{1}{3}$.
Answer: $\displaystyle\frac{1}{3}$.
Implicitly you have inverted the result of usual third step. This inversion of a proportion is Invertendo.
How would you know that Componendo dividendo is to be applied?
Before solving the last example problem, let us define a very important requirement for using the Componendo dividendo rule successfully. This will provide the answer to a very basic question,
How do you know when to use the Componendo dividendo rule?
You would know for sure when to use the rule by detecting the Signature of Componendo dividendo.
The following involve advanced concepts which would help you to attain a high level skill in solving difficult problems quickly and elegantly by Componendo dividendo.
Identify the signature of Componendo dividendo to know when to apply the rule
A specific pattern in the terms of a ratio in the given equation or in the desired expression generally identifies that the problem can be quickly solved by using Componendo dividendo rule.
This signature of Compoendo dividendo in the ratio is of the form,
$\displaystyle\frac{a+b}{a-b}$ or $\displaystyle\frac{a-b}{a+b}$, where $a$ and $b$ are elementary variables or compound variables representing expressions.
In this signature form of the ratio, both numerator and denominator must have exactly same two terms but of opposite sign between the numerator and denominator.
Examples are,
Example 1: $\displaystyle\frac{5a+7b}{5a-7b}$.
By Componendo dividendo you would get, $\displaystyle\frac{5a}{7b}$ or $\displaystyle\frac{7b}{5a}$.
Example 2: $\displaystyle\frac{a-3b+9c}{a+3b+9c}$.
By Componendo dividendo you would get, $\displaystyle\frac{a+9c}{3b}$. In this case one of the two variables is compound, $(a+9c)$ and the second elementary, $3b$.
Example 3: $\displaystyle\frac{1+\sec \theta+\tan \theta}{1-\sec \theta+\tan \theta}$.
The two terms same in numerator and denominator are,
$1+\tan \theta$, a compound variable, and,
$\sec \theta$.
Observe,
All the elementary variables are trigonometric functions. But that won't stop you from applying the Componendo rule as the rule is basically algebraic (operating on abstract variables).
By Componendo dividendo you would get,
$\displaystyle\frac{1+\tan \theta}{\sec \theta}=\sin \theta +\cos \theta$, a much simplified result.
Problem example 3. Componendo dividendo in Trigonometry
If $a=\sec \theta+\tan \theta$, then $\displaystyle\frac{a^2-1}{a^2+1}$ is,
- $\sec \theta$
- $\cos \theta$
- $\tan \theta$
- $\sin \theta$
Solution to Problem example 3. Problem analysis
The target expression is in perfect form for applying Componendo and Dividendo only if instead of $a$, we were given the value of $a^2$.
So instead of thinking of applying Componendo Dividendo, now we look for ways to transform the input value of $a$ to $a^2$. This is what we call Analytical approach example in which to get the given target we determine how we need to transform given input. Our immediate action changes accordingly.
Solution to Problem example 3. Problem solving execution
We achieve this immediate goal by using a special property of what we call one of the golden trigonometric function pairs, that is, $\sec \theta$ and $\tan \theta$. The property is,
$sec \theta + tan \theta = \displaystyle\frac{1}{sec \theta - tan \theta}=a$, in this problem.
The property is true because,
$sec^2 \theta - tan^2 \theta=1$, and $a^2-b^2=(a+b)(a-b)$.
Thus we get the value of $a^2$,
$a^2=\displaystyle\frac{sec \theta + tan \theta}{sec \theta - tan \theta}$.
And finally, applying the componendo dividendo on the equation (subtracting 1 from both sides, again adding 1 to both sides of the original equation and taking the ratio of the two),
$\displaystyle\frac{a^2-1}{a^2+1}=\frac{tan\theta}{sec\theta}=sin\theta$.
Answer: Option d: $sin \theta$.
Just remember, in solving tough problems,
You need to think analytically more rather than just apply a method mechanically.
Observe that we had to get value of $a^2$ before applying Componendo dividendo as that is the main variable in the pattern of Componendo dividendo in the target expression.
With right approach and techniques the problem could easily be solved mentally.
Componendo dividendo ensures that a problem can be solved in mind taking minimum time.
Applications of Componendo dividendo
We have used Componendo dividendo extensively for solving many difficult Quantitative Aptitude problems in algebra, trigonometry, numbers, surds, ratio proportion and so on.
This is by far the single most powerful general purpose method that can give you the solution in no time.
The articles below explain how varieties of problems can be solved ultra-quick by applying Componendo dividendo.
Resources on Componendo dividendo
You may like to go through the related tutorials,
Componendo dividendo uncovered to solve difficult algebra problems quickly 5
Componendo dividendo applied in number system and ratio proportion problems
Componendo dividendo explained