
Maxima minima of trigonometric expressions, linear and quadratic
How to find Maxima minima of trigonometric expressions comprehensively covered. Also covered maximum and minimum values of trigonometric expressions.
The sections are,
- Maximum and minimum values of trigonometric functions.
- Interim goal for finding maxima minima of trigonometric expressions.
- How to convert a sum of two trigonometric functions $a\sin \theta+b\cos \theta$ to a single term trigonometric function.
- How to find maxima minima of $a\sin \theta +b\cos \theta$.
- How to find maxima minima of $a\cos \theta - b\sin \theta$.
- How to find maxima minima of quadratic trigonometric expression $2\sin^2\theta+3\cos^2\theta$.
- How to find Maxima minima of $\sin {\theta}\cos \theta$ and its powers
- AM GM inequality.
- How to use AM GM inequality to find minima maxima of $7 tan \theta +8 cot \theta$.
You may click on any of the above section links and after reading the section, return by clicking the browser back button.
Maximum and minimum values of trigonometric functions
You can yourself derive the maximum and minimum values of six trigonometric functions from the trigonometric value table for specific angles.

Maximum and minimum values of $\sin \theta$ and $\cos \theta$
From the table it is clearly seen that maximum and minimum values of both $\sin \theta$ and $\cos \theta$ are $1$ and $-1$. For all other angles, values of these two fundamental trigonometric functions vary between $1$ and $-1$.
You will get a better idea on the maximum, minimum and other values of $\sin \theta$ and $\cos \theta$ from the following figure.

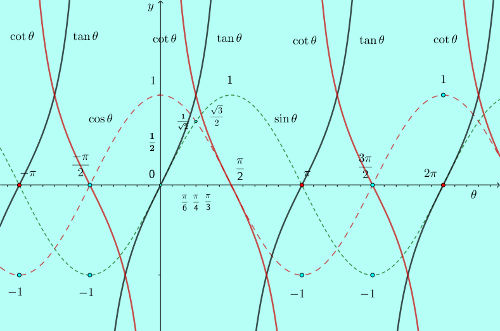
Maximum and minimum values of $\tan \theta$ and $\text{cot }\theta$
The truth is,
There is no maximum or minimum values for $\tan \theta$ and $\cot \theta$.
We may state the situation in a slightly different way. When $\sin \theta$ approaches 1 while $\cos \theta$ in the denominator approaches zero,
Maximum value of $\tan \theta$ tends to $\infty$ but it cannot be defined.
Get an idea of the maximum, minimum and variation of values of $\tan \theta$ and $\cot \theta$ from the following figure,
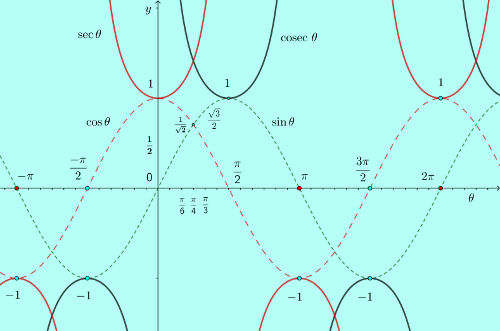
Maximum and minimum values of $\sec \theta$ and $\text{cosec } \theta$
$\sec \theta$ and $\text{cosec } \theta$ being inverses of $\cos \theta$ and $\sin \theta$ both with 0 value for some values of $\theta$, these two functions also do not have any maximum or minimum value that can be defined.
Get an idea of variation of values of these two trigonometric functions from the following figure,
Interim goal for finding maxima minima of trigonometric expressions
We will first consider the problem of finding maximum value of the two term expression,
$a\sin \theta + b\cos \theta$.
The individual functions of $\sin \theta$ and $\cos \theta$ change periodically with change of $\theta$ in exactly the same manner except that, broadly speaking, when $\sin \theta$ reaches maximum value, $\cos \theta$ reaches value 0. In formal terms we say, $\cos$ function lags behind in phase from $\sin$ function by $90^0$.
The following curves give an idea of the behavior of two trigonometric terms, $y=3\sin x$ and $y=2\cos x$, plotted on the same graphing layout.

Though each term individually oscillates between fixed maximum and minimum values, when the values of the two terms are summed up, finding out the maximum or minimum of the resulting expression turns out to be confusing and difficult.
We can see though, if somehow the two term expression is transformed to a single trigonometric function with suitably changed coefficient, we can easily determine the maximum (or minimum) value of the sum expression from the maximum (or minimum) of the equivalent single trigonometric term.
This in fact is the most important intermediate goal in the process of finding the maxima or minima of ANY trigonometric expression,
Transform the given expression to an equivalent expression in a single term trigonometric function with a suitably evaluated co-efficient.
While transforming the given expression, the suitable coefficient is automatically generated with the single function of $\sin$ or $\cos$. The angle base of this function will be different from the angle base of the functions in the original expression, but having a single function will have the great advantage of directly getting its maximum value from trigonometric function behavior. Multiplied with the co-efficient we get the maxima or minima of the given expression straightaway.
How to convert the expression $a\sin \theta +b\cos \theta$ to a single term trigonometric function
The direct path to transform the two term expression to a single term is to use the compound angle relationship,
$\sin (A+B)={\sin A}\cos B + {\cos A}\sin B$
The expression to be transformed to a single term function is,
$a\sin \theta + b\cos \theta$,
Let us assume,
$a=c\cos \alpha$, and,
$b=c\sin \alpha$.
These two assumptions automatically relate $a$ and $b$ through the common element $c$,
$a^2+b^2=c^2$.
Geometrically we can represent this relationship between $a$, $b$ and $c$ in a right triangle with two perpendicular sides as $a$ and $b$ and the hypotenuse as, $c=\sqrt{a^2+b^2}$,

We are now in a position to define $\alpha$ in terms of $\tan \alpha=\displaystyle\frac{b}{a}$, so that,
$a\sin \theta + b\cos \theta$
$=c\cos {\alpha} \sin \theta + c\sin {\alpha} \cos \theta$
$=c\left(\cos {\alpha} \sin \theta +\sin {\alpha} \cos \theta\right)$
$=c\sin (\theta +\alpha)$.
The coefficients $a$, $b$ and $c$ are related through the right triangle with base angle $\angle \alpha$.
Note: For detailed concepts on compound angle functions you may refer to our session on Trigonometry concepts part 2, compound angle functions.
How to find maxima minima of linear additive trigonometric expression $a\sin \theta + b\cos \theta$
So we have achieved the first goal of transforming the two term trigonometric expression to a single term function.
At this point it is easy to see that the maxima of $a\sin \theta +b\cos \theta$ will occur when $\sin (\theta +\alpha)$ reaches its maxima which is 1.
So the maximum value of the expression is,
$\text{Max }[a\sin \theta + b\cos \theta]=c=\sqrt{a^2+b^2}$.
Ultimately it is a simple expression.
Minima of $a\sin \theta + b\cos \theta$
Minima of the target expression will occur simply when $\sin (\theta +\alpha)$ is minimum, which is $-1$.
So,
$\text{Min }[a\sin \theta + b\cos \theta]=-c=-\sqrt{a^2+b^2}$.
How to find maxima minima of linear subtractive trigonometric expression $(a\cos \theta - b\sin \theta)$
For this expression we need to use the compound angle relation,
$\cos (\theta+\alpha)=\cos {\theta}\cos \alpha - \sin {\theta}\sin \alpha$.
We will take,
$a=c\cos \alpha$, and
$b=c\sin \alpha$.
Substituting these two in $(a\cos \theta - b\sin \theta)$,
$(a\cos \theta - b\sin \theta)$
$=c\left(\cos {\theta}\cos \alpha - \sin {\theta}\sin \alpha\right)$
$=c\cos(\theta+\alpha)$.
In this case also, maximum value of $\cos(\theta +\alpha)$ is 1 and $c=\sqrt{a^2+b^2}$.
How to find maxima minima of quadratic trigonometric expression $2\sin^2\theta+3\cos^2\theta$
In this case the method is exactly same in so far as the intermediate step of converting the expression to a single function expression is concerned. The difference lies in how we carry out the all-important transformation.
The target expression to be transformed is,
$2\sin^2\theta+3\cos^2\theta=2+cos^2\theta$
Because of the convenience of using the identity, $\sin^2 \theta+\cos^2 \theta=1$, we didn't have to use compound angle relationship to transform the target expression into an expression involving a single trigonometric function.
As absolute value both of minima and maxima for $\cos \theta$ is 1, squaring removes the minus sign, and maximum value of $\cos^2 \theta$ turns out to be 1.
So,
$\text{Max }[2\sin^2\theta+3\cos^2\theta]$
$=\text{Max }[2+\cos^2\theta]$
$=2+\text{Max }[\cos^2\theta]$
$=2+1=3$
Minima of quadratic expression $2\sin^2\theta+3\cos^2\theta$
The minima occurs when the $\cos^2 \theta$ function reaches minima, which is 0, as negative values are squared into positive sign.
Thus,
$\text{Min }[2\sin^2\theta+3\cos^2\theta]$
$=\text{Min }[2+\cos^2\theta]$
$=2+\text{Min }[\cos^2\theta]$
$=2+0=2$.
These are all based on fundamental trigonometric concepts, and being confined in the domain of trigonometry itself, may be felt to be more attractive. But the fact remains that in conjunction with the above concepts if we use the Artificial Tool of AM GM inequality from Algebra topic domain, many of the otherwise difficult maximizing (or minimizing) problems of this class can be solved quickly and easily.
Let us first state AM GM inequality and offer a brief proof.
How to find maxima minima of $\sin {\theta}\cos \theta$ and its powers
Here also we need to use the compound angle relationship,
$\sin 2\theta=\sin (\theta +\theta)$
$=\sin {\theta}\cos\theta +\cos {\theta}\sin \theta$
$=2\sin {\theta}\cos \theta$,
Or, $\sin {\theta}\cos \theta=\frac{1}{2}\sin 2\theta$.
This is the guiding relationship that will determine the maxima or minima of $\sin {\theta}\cos \theta$ and its powers.
In general, the maxima for all even powers of $\sin {\theta}\cos \theta$ is,
$\text{Max}\left[\left(\sin {\theta}\cos \theta\right)^{2n}\right]$, where $n$ is a natural number
$= \left(\frac{1}{2}\right)^{2n}\left(\text{Max}[\sin 2\theta]\right)^{2n}$
$=\left(\frac{1}{2}\right)^{2n}\left(1\right)^{2n}$
$=\left(\frac{1}{2}\right)^{2n}$.
But for evaluating the minima for all even powers of $\sin {\theta}\cos \theta$ we cannot take the minimum value of $\sin 2\theta$ which $-1$ because it will then result in the same maxima and minima for the expression for even powers of the expression.
Instead we need to consider 0 value of the $\sin 2\theta$ for evaluating the minima of the LHS expression. Thus minima for even powers of $\sin {\theta}\cos \theta$ is,
$\text{Min}\left[\left(\sin {\theta}\cos \theta\right)^{2n}\right]=0$
On the other hand, though the maxima for all odd powers of $\sin {\theta}\cos \theta$ will be same as the maxima for even powers, the minima for odd powers will be,
$\text{Min}\left[\left(\sin {\theta}\cos \theta\right)^{2n+1}\right]$
$=\left(\frac{1}{2}\right)^{2n+1}\left(-1\right)^{2n+1}$
$=-\left(\frac{1}{2}\right)^{2n+1}$.
AM (Arithmetic Mean) GM(Geometric Mean) inequality
Arithmetic Mean or AM of the two terms of $x+y$
The AM of the two terms in the two term (for simplicity and relevance to our class of problems) expression, $x+y$ is,
$\text{AM}=\displaystyle\frac{x+y}{2}$
This is also known as average of the terms where the terms are summed up and the sum divided by the number of terms.
The two terms $x$ and $y$ with the AM in between form an Arithmetic Progression or AP, where difference between any two consecutive terms is same.
In the three term series,
$x$, $\displaystyle\frac{x+y}{2}$ and $y$
the difference between the second and first terms is,
$\displaystyle\frac{x+y}{2}-x=\displaystyle\frac{y-x}{2}$.
Similarly the difference between the third term and the second term is,
$y-\displaystyle\frac{x+y}{2}=\displaystyle\frac{y-x}{2}$, which is same as the previous difference.
Geometric Mean or GM of the two terms of $x+y$
The Geometric Mean or GM of the two terms $x$ and $y$ in the expression $x+y$ is,
$\text{GM}=\sqrt{xy}$.
Geometric Mean of the two terms $x$ and $y$ forms the middle term of a Geometric Progression or GP of three terms,
$x$, $\sqrt{xy}$, and $y$.
These three terms form a GP as each term is multiplied by the fixed value of $\sqrt{\displaystyle\frac{y}{x}}$ to get the next term, which is the basic characteristic of a GP.
Note: Verify this yourself.
AM GM inequality
The frequently used inequality states mathematically,
$\text{AM} \geq \text{GM}$.
Let us see how this happens with the two terms of our expression, $x+y$.
We have,
$(x-y)^2\geq 0$,
Or, $x^2-2xy+y^2 \geq 0$,
Or, $x^2+2xy+y^2 -4xy \geq 0$,
Or, $(x+y)^2 -4xy \geq 0$,
Or, $(x+y)^2 \geq 4xy$,
Or, $\displaystyle\frac{x+y}{2} \geq \sqrt{xy}$,
Or, $\text{AM} \geq \text{GM}$.
Only when $x=y$, the equality occurs. Otherwise,
$\text{AM} \gt \text{GM}$.
In general,
$\text{AM} \geq \text{GM}$.
Let us see how this powerful but simple inequality can be used for finding maxima or minima of trigonometric expressions. As an example we will take up minimizing the expression,
$7 \tan \theta +8 \cot \theta$.
How to use AM GM inequality to find maxima minima of $7 tan \theta +8 cot \theta$
The expression under consideration is,
$7 \tan \theta +8 \cot \theta$.
So the AM is,
$\text{AM}=\displaystyle\frac{7 \tan \theta +8 \cot \theta}{2}$.
The GM is,
$\text{GM}=\sqrt{56}$.
By the AM GM inequality then,
$\displaystyle\frac{7 \tan \theta +8 \cot \theta}{2} \geq \sqrt{56}$,
Or, $7 \tan \theta +8 \cot \theta \geq 4\sqrt{14}$.
This inequality states that the value of the expression on the LHS can only be greater than or equal to the value in RHS.
This means the minimum value of the expression $7\tan \theta +8\cot \theta$ is,
$4\sqrt{14}$.
The basic inequality concept has been used here.
Note: The given expression doesn't have any defined maximum as either of the terms have maximum value undefined as $\infty$.
Recommendation
There are many variations to this class of problems. In general for all such problems the overriding goal is to transform the expression to an expression involving a single trigonometric function. Wherever possible we need to use the AM GM inequality in addition or in isolation as required.
Guided help on Trigonometry in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Trigonometry in Suresolv, follow the guide,
The guide list of articles is up-to-date.