
How to Connect 9 Dots with 4 Lines Without Revisiting a Dot or Lifting the Pencil
Discover the secret to solving Connect the Nine Dots Riddle with our detailed step-by-step guide. Master Problem-solving skills and Inventive thinking.
Connect the Nine Dots With 4 Lines Riddle
Join the nine dots in a 3-by-3 two-axis grid by 4 straight lines without visiting a dot more than once and without raising your pencil from the paper. The nine dots are on a plane surface.
Time to solve: 30 minutes.
The nine dots in a 3-by-3 two-axis grid shown.

Hint: The puzzle is hard and demands out-of-the-box thinking. To solve this puzzle, you must take a totally unconventional route, unless you are a genius who solves such inventive puzzles instinctively.
Connect the nine dots riddle solution: Analysis and strategy decision
Try connecting the nine dots a number of times to realize the puzzle cannot be solved with the conventional approach of random trial and error.
In most attempts, you would either need 5 or more lines or you'll leave a dot unconnected if you use 4 lines. The only way to approach solving this hard puzzle must be to:
- Analyze an invalid solution to understand in-depth why it is invalid and identify important patterns hidden to any casual inspection.
- Draw conclusions and form strategies that must be followed for solving the puzzle.
This is the analytical path using logical reasoning.
For analysis, take up a simple way to connect all 9 dots.
Trial connection with 5 lines: To analyze and know more about the problem. This is intelligence gathering, as is often done in prototyping.
How to Solve Connect the Nine Dots Riddle: first trial to know more about the complexity of the puzzle
As the first experiment, join the nine dots using each line to connect the maximum number of dots as far as possible. These are the three vertical lines. But, to connect the three dot-joining lines two more lines are needed making the solution invalid.
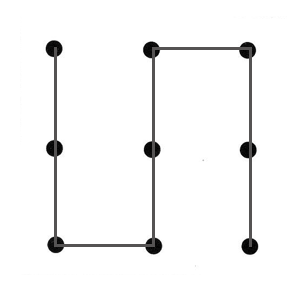
Observations and identification of the most important strategy to follow:
- The vertical dot-joining lines are the more important ones, while the two extra horizontal lines to connect the vertical lines are wasteful.
- The dot-joining lines are primary and the two extra lines are secondary. These secondary lines are wasteful, making the solution invalid.
Strategy to follow: Reduce the number of secondary lines as far as possible. Number of secondary lines to connect the primary lines that join the dots should be zero.
With a focus on reducing the number of secondary lines at every step, examine how the lines help in reducing wasteful secondary lines. Only two types of lines can be used: Vertical (or Horizontal) lines and Oblique lines:
- The vertical or horizontal lines are similar as any two vertical (or horizontal) lines need an extra line to connect the two.
- But, an oblique dot-joining primary line directly connects to the next primary line. This saves the need for an extra line.
Conclusion: The ultimate solution must include this most efficient way of connecting three dots—an oblique diagonal.
To try out the new ideas, make a second experiment.
Connect the nine dots riddle: Understand more about a Diagonal—Connect it with more dots
Where should the joining pencil move after joining three diagonally placed dots forming a diagonal straight line?
- Answer: It can move either horizontally or vertically connecting directly with the next dots, needing no extra secondary line.
The result:

This formation connecting 5 dots with only 2 straight lines is the most efficient way of connecting 5 dots. So, it must be a part of any solution—it is an essential formation in a solution.
Connect the remaining 4 dots with the 5-dot essential formation—Meet the insurmountable barrier
Make a third trial with the objective of further analysis:
Connect the rest 4 dots with the 5-dot essential formation in the simplest manner—dot by dot.

Number of lines 6—invalid solution.
While you are confident that the 5-dot formation is flawless, connecting the remaining 4 dots with only two lines poses a significant challenge.
This is the insurmountable barrier to the solution.
To overcome it, you must discover an innovative new way. Conventional thinking won’t work—you must think out-of-the-box.
You realize something vital is missing. The only logical path forward is to question every assumption you’ve made about the problem.
Property Analysis to Discover a Taken-for-granted Property
What are you missing? About what?
Consider this: What is the most important object you’ve been using all along? It’s the straight lines that connect the dots.
This realization leads to the first breakthrough:
You must be missing something about the dot-joining lines themselves. Identify this as the object to analyze.
To discover what you have assumed about the dot-joining lines without being aware, first
- List all things that you know about a dot-joining line. These are the properties of the primary object:
- A dot-joining line must be straight—known.
- All joining lines must be on a plane—also known.
Anything else about a dot-joining line? Did we take any property for granted and forgotten that we can change the property? Focus on this single point. It may take a while, but focusing intensely on a single point, you will discover the ignored details.
You wonder: Do we have to draw a line always inside the 3-by-3 grid-box? Is it a must? Insistent questioning brings out the novel idea. The property that remained invisible reveals itself,
- Property taken-for-granted: The dot-joining lines to be drawn only inside the 3-by-3 grid—along the periphery, though this wasn't a puzzle restriction.
The restricting grid-box:
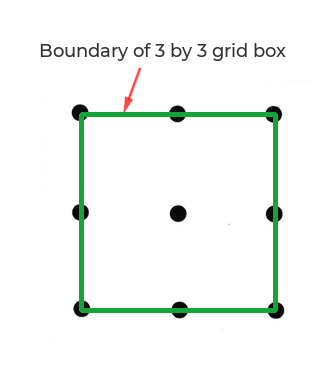
Can’t a dot-joining line pass over a dot at the border and continue outside the grid-box to connect with a second extended line! Surely it can. No restriction on it.
More importantly,
If two primary lines continue beyond the grid-box and join each other, it saves a precious extra line for linking the two.
Realize: This must be the most important change in property of a dot-joining line—ability to be extended beyond the grid-box. So,
At the least, two lines must continue beyond the last dot joined and move out of the grid. This is because, the second beyond-the-grid-line must join with the first to bring it back to the safe confines of the grid-box.
Last task in the solution: Joining the rest two pairs of dots
To make analysis easier, the dots are numbered:

Start with solution fragment: The pencil starts from dot 1, connects 5 dots and stops at dot 3. Four dots still to connect to this must-be-included part.
Analyze segment by segment (this is breaking up a problem into smaller parts).
Join the 4 remaining dots by independent line segments first and then connect the segments.
How many line segments are needed to join these 4 dots?
Realize: The only way to join two pairs of dots separately, is by two independent line segments. The number cannot be 1 or 3.
Joining the two remaining pairs of dots,
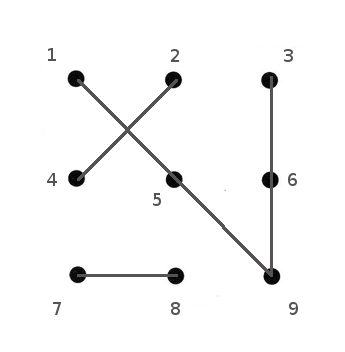
Last challenge is to connect the four line segments.
Solution: Last stage of joining the line segments
Realize:
- Nine dots are already joined by four line segments. Quota of line segments exhausted. The segments must be joined using no more line segments.
How to connect line segment 2-4 with line segment 8-7?
- Intermediate Solution: Extend line segment 2-4 and line segment 8-7 till the two meet at a point outside the grid-box. You have used your new freedom of extending a line out of the grid-box.

The two pairs of connected line segments are to be joined now.
Better expressed, the problem reduces to connecting dot 2 with dot 3 using no more line segment. And that is easy:
Extend line segment 4-2 and line segment 6-3 to meet at a point outside the grid-box.
Ultimate solution:

All four connecting lines move out of the grid-box to get joined with each other. Truly an out-of-the-box solution.
Where should the connecting pencil start? Two choices:
Connecting the dots may start at dot 1 and end at dot 8 OR it may start at dot 8 and end at dot 1. Both are the same.
How many solutions?
An alternative is to start by connecting the diagonal 3-5-7.
This seems to be a second solution. Think again. If you rotate one of the two, it coincides perfectly with the other:
Only one rotationally unique solution possible.
Summing up
The critical breakthrough in this hard inventive puzzle emerged beyond conventional thinking. It came through the property analysis of dot-joining lines, the primary object of attention, persistently driven by the intent to uncover hidden patterns.
As we tried to identify the taken-for-granted, invisible property of dot-joining lines that formed the inventive barrier or gap, we experienced something remarkable. The ability to literally and actually move out of the box:

It challenged our preconceived notions and opened up a new possibility, the heart of the inventive solution.
Try the inventive technique when you face an impenetrable barrier while solving a hard problem, in academics or in real-life.
At the end
Connect the nine dots riddle existed long before it appeared in Sam Loyd's Cyclopedia of Puzzles in 1914. It is thought to be the origin of the expression "thinking outside the box". To my knowledge, the solution of only this puzzle shows literally and actually what out-of-the-box thinking is.
The classic riddle is truly one of a kind with no easy intuitive solution. Random trial is harder, if not impossible. Solution needs the elusive out-of-the-box thinking sought by all.
In this solution, the inventive Property Change Analysis Technique is used for leaping across the inventive gap onto the out-of-the-box unthought-of possibility.
If you are more interested
Some complexities of the human mind revealed by solution attempts of this puzzle:
- Most Wanted Solutions: 9 Dot puzzle - Archimedes-lab.org: This is a very interesting read for all who want to know about the psychology of inventive thinking. The solution doesn't depend on maths.
- Nine dots puzzle: Wikipedia: Focus is on maths and complexity. No mention of human reasoning or inventive thinking.
- 9 Dots Puzzle: How to Connect 9 Dots with 4 Lines?: Solution is brief. From the embedded resource links, get a glimpse of how weird can human thinking be!
Know how to solve difficult problems easily without wasting time on random attempts
Our ebook on puzzle solutions by innovative methods will show you just that.
Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving
BUY the eBook Amazon Kindle version here, from Google Play here and Paperback here.
More puzzles to enjoy
From our large collection of interesting puzzles enjoy: Maze puzzles, Riddles, Inventive puzzles, Paradoxes, Mathematical puzzles, Logic puzzles, Number lock puzzles, Missing number puzzles, River crossing puzzles, Ball weighing puzzles and Matchstick puzzles.
You may also look at the full collection of puzzles at one place in the Challenging brain teasers with solutions: Long list.
Enjoy puzzle solving while learning problem solving techniques.
