Find the fake ball among 9 identical balls in 3 weighing puzzle

Find the fake ball in 3 weighs—9 balls 1 different weight puzzle

Find the fake ball among 9 balls in 3 weighs. All balls look alike. You have a pan balance with no weights. Time to solve is 30 minutes.

Give it a try before going ahead.

Bonus puzzle

Can you find all possible ways to solve the puzzle?

No time limit for this one and no solution from us. It’s only for you, if you are curious.

Solution to the 9 balls 1 different weight puzzle: Find the fake ball in 3 weighs

What should be the best plan for first weighing? We can’t divide 9 into two equal parts; so obviously,

there has to be three parts: two equal sized sets of balls weighed against each other and a third set of balls left aside.

Next question pops up at once,

how best 9 is to be split up into 3 parts?

Mentally explore what happens if you keep just 1 ball aside and weigh 4 balls against other 4. In the best case, the scale will be perfectly balanced proving that all 8 balls weighed are good balls and the 1 left aside ball is the fake one. Just weigh the fake ball with 1 out of 8 good balls and you will know whether the fake ball is lighter or heavier than the good balls.

But if such a good fortune doesn’t smile on you, you’ll have 8 suspect balls, either the fake among the 4 lighter or among the 4 heavier ones.

This path is not promising at all and we’ll follow a general principle of problem solving drawn from experience on how best to divide and conquer,

Divide the enemy in the smallest sized groups with group sizes as same to each other as possible.

All the three group sizes to be smallest and similar, 9 is to be split into three groups each with 3 balls,

9 = 3 + 3 + 3.

This strategy also follows principle of symmetry,

If you increase the symmetry in the problem by an action, that will be your MOST PROMISING ACTION.

We promptly decide to weigh first,

3 balls against 3 others—6 balls with 3 balls kept aside.

The figure shows the first weighing combination.

Three outcomes of the weighing are possible:

1. First result of 1st weighing—the right pan descends.

Conclusion: All six balls are suspect. Specifically,

1.1. Either the left side up-going three balls contain the fake lighter ball, or,

1.2. The right side descending pan has the fake heavier ball.

The picture below shows the situation.

2. Second possibility—the left pan descends:

Conclusion: All six balls are suspect. Specifically,

2.1. Either the left side descending three balls contain the fake heavier ball, or

2.2. The right side up-going pan has the fake lighter ball. Essentially, these two results will need exactly similar actions as the results 1.1 and 1.2.

We won’t analyze these two results further. Analyzing results 1.1 and 1.2 should be enough for reaching the solution.

3. Third possibility—the pans are equally balanced:

Conclusion:

The three left aside balls must contain the fake ball and,

All six balls weighed are good balls.

Let’s take up the third result first.

Exploring third result of 1st weighing: Finding the fake ball among 3 left aside suspect balls in 2 weighing

Second weighing combination for 3rd result:

Add 1 good ball from 6 to the three suspect kept aside balls and weigh 2 against 2. Out of 6 good balls, five are not used.

The following schematic shows this weighing combination. The suspect balls are shaded.

One side must go down.

Result 3.1. When the pans were equally balanced in 1st weighing AND the pan with 1 good ball descends in 2nd weighing:

3.1.1. Either the single suspect ball with the good ball (shaded and marked L) is heavier,

3.1.2. Or, the two right pan balls (shaded and marked R) has the fake lighter one.

You are not totally sure yet, but one weighing is still left with you.

Third weighing scheme for result 3.1:

Weigh two suspect balls in right pan against each other—shaded R against the other shaded R. One of these may be the fake lighter ball.

This is shown in the following schematic.

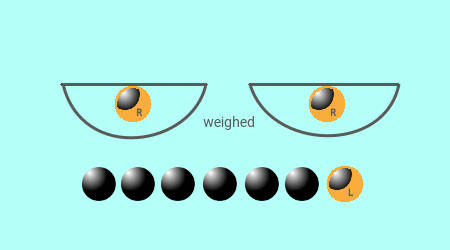
Final Conclusions from 3rd weighing for Result 3.1

Only two possible conclusions are,

1. The pan going up has the fake lighter ball, if the two pans do not balance each other.
2. The single suspect ball left out in the 3rd weighing is the fake heavier ball, if the two pans balance.

First is in the figure left and the second is in figure right.

Result 3.2: When pans are equally balanced in 1st weighing AND pan with 1 good ball goes up in 2nd weighing

Here also you will take exactly the same action of weighing the two balls in right pan against each other. Only the results and conclusions will be reverse to the results we had just now.

Time to analyze the first result of 1st weighing.

Find fake ball in 9 balls by 3 weighs puzzle: Exploring 1st result of 1st weight when left pan with 3 balls went up

The schematic of Result 1 of first weighing is shown for convenience.

And the conclusion: All six balls are suspect. Specifically,

1.1. Either the left side up-going three balls contain the fake lighter ball,

1.2. Or, The right side descending pan has the fake heavier ball.

All six suspected fake balls are shaded with up-going left pan balls marked L and descending right pan balls marked R for ease of later reference.

Analysis and weighing decision for the second weighing for two groups of 3 suspect balls each

We have to think out of the box. The number of suspect balls is as large as 6. Points in our favor are:

1. The left pan fake ball must be lighter and the right pan fake ball must be heavier and,
2. Three left out balls are good balls.

First decision taken to balance the up-going and descending situation partially is,

To EXCHANGE 1 ball between the two pans.

This is a variation of much used base equalization technique used in solving math problems at high speed. This action balances the asymmetry of nature of ball weights and increases the overall symmetry.

The second decision taken to reduce the number of possible results of second and third weighing is,

To KEEP ASIDE 1 ball from each pan.

Dividing 6 suspect balls into three groups each with 2 balls follow our earlier strategy,

This reduces the size of three parts of 6 to 2, 2 and 2, and this is the smallest size of the part groups.

The second weighing combination is shown.

In this second weighing, each pan has exactly same combination of ball types,

Each pan has one L marked ball that can only be the lighter one if found fake, and one R marked ball that can only be the heavier one if found fake.

Results of 2nd weighing for the 1st result of 1st weighing: left pan went up and all 6 balls were suspect

There can be three possibilities,

1. Left pan again goes up—Conclusion: Either left pan L ball is the lighter fake, Or, the right pan R ball is the heavier fake,
2. Left pan descends this time—Conclusion: Either right pan L ball is the lighter fake Or, the left pan R ball is the heavier fake, and
3. The two pans are perfectly balanced—Conclusion: Either the kept aside L ball is the lighter fake Or, the kept aside R ball is the heavier fake.

Conclusions point out to the same result in all three cases—one of two L-R pair of balls is the fake.

Final 3rd weighing and solution of 9 balls puzzle for 1st result in 1st weighing: left pan went up and all 6 balls were suspect

The last step is easy,

Just weigh a good ball against any of the suspect L-R pair of two balls.

The weighing combination is shown,

An L-ball is placed again on left pan and a good ball in right pan and last weigh done.

There can only be two results and consequent conclusions:

If left pan goes up, the L-ball in it is the fake ball, and,

If the two pans balance perfectly, the kept aside R-ball is the fake heavier ball.

Parting Question: Can you solve the puzzle in a different way?

If you explore to find the answer, you may discover new ways to solve this not so easy puzzle, and also you will understand why we took a composite action of exchanging and keeping aside balls simultaneously.

---

Know how to solve difficult problems easily without wasting time on random attempts

Our ebook on puzzle solutions by innovative methods will show you just that.

Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving

(BUY from Apple books, Barnes & Noble, Rokuten Kobo, Vivlio, Angus & Robertson, Tolino, PayHip and others)

BUY the eBook Amazon Kindle version here, from Google Play here and Paperback here.

Second book on Innovative Solutions to Matchstick Puzzles from Suresolv

BUY Creative Matchstick Puzzles Innovative Solutions eBook Amazon Kindle version

BUY the paperback here.

 

---

Puzzles you may enjoy

Easy to hard brain teasers with systematic solutions

Challenging brain teasers with solutions: Long list.

This will always be the most up-to-date full list with the brain teasers classified into categories that can be browsed separately.

You may also click on the category term link below to enjoy the brain teasers that are classified in the present category.

For example, if the category term link shown below is "Riddle", click on it to go through all the Riddles.

---