How many addition signs should be put between digits of 987654321

Additions signs to be placed between digits of 987654321 to make sum 99

How many addition signs should be put between digits of 987654321 to equal 99? Where should they be placed? Time to solve 10 minutes.

This is the main puzzle.

Second puzzle: Use digits 1 to 9 only once each to form numbers, sum of which will be 99. How many ways can you do it?

Third puzzle: Use digits 1 to 9 only once each to form numbers, sum of which will be 99. How many such combinations can you form using minimum number of addition signs?

For the second and third part of the puzzle there is no time limit.

Remark: The puzzle is adapted and expanded from a MT Calendar math problem.

Hint: Don't try randomly testing out possibilities. Go for discovering a binding rule or pattern in the puzzle and use it fully for the solutions step by step.

Systematic step by step solution to the Main puzzle: How many addition signs should be put between digits of 987654321

The puzzle

How many addition signs need to be placed between the digits of the number 987,654,321 to make the total 99?

To solve the puzzle, we will ask a series of questions (to ourselves), analyze to get answer and make conclusions. This is the powerful Question, analysis and answer method of problem solving with broad scope of applications.

But first we will define the problem more precisely, bringing out requirements that were implicit. This is always the first step in systematic problem solving.

Precise problem definition by analyzing the problem description

When you place addition signs between the digits of the 9 digit number $987,654,321$, the 9 digits are split into a few parts sum of which is 99. For example, if you place 8 addition signs between the 9 digits, the result would be,

$9+8+7+6+5+4+3+2+1=45$, much less than 99.

By this simple example, you realize that the 9 digits cannot be completely split into 9 parts of single digits.

Conclusion 1: At least one of the parts must be a 2 digit number.

This is discovery of the first pattern or rule that will help to solve the puzzle.

It means more clearly,

Conclusion 2: The addition signs are to be placed between the digits to split the sequence of 9 digits into parts that will be single digit or two digit numbers.

A third rule that is implicit in the problem definition should be clear,

Conclusion 3: The sequence of the digits must not be altered.

The last conclusion is implicit but strictly to be followed as in the problem you are asked to place the addition signs between the digits of the number $987,654,321$ in a given sequence, and not between 9 digits from 1 to 9 with any ordering.

Stage 2 Solution to the main puzzle: How many addition signs should be put between digits of 987654321: Question analysis answer

Realizing that at least 1 two digit number must be there in the solution sum, we ask the first important question,

Question 1: Assuming only 1 two digit number in the solution sum, is it possible for any of the 8 digits to be the tens digit of the two digit number? As 1 is the last in the series of 9 digits it is ignored from consideration.

Analysis for answer 1: Obviously, 98 with 9 as tens digit, 87 with 8 as tens digit are infeasible as sum of the rest of the single digit numbers when added to the two digit numbers will far exceed 99.

We are not sure offhand about 76, and so will test 76 with 7 as tens digit,

For 76: Sum of rest of the digits added to 76 is,

$9 + 8+76+5+4+3+2+1=108$, exceeding 99.

So 76 as a possible two digit number is infeasible and we will test 65 next,

For 65: Sum of rest of digits added to 65 is,

$9+8+7+65+4+3+2+1=99$.

Well, well, well. You have hit upon the solution so quickly! With a just a bit of analysis and method along with systematic trial.

Answer: 7. You will need exactly 7 addition signs that are to be placed between 9 and 8, between 8 and 7, between 7 and 65, between 65 and 4, between 4 and 3, between 3 and 2, between 2 and 1.

First part of the puzzle solved in no time.

We'll not carry out any elaborate analysis about the interesting properties that are inherent in the puzzle just now, but yes, the highly interesting aspects will be uncovered while solving the second and the third puzzle.

Let us solve the second and third parts of the puzzle.

Comment: If you compare the main description of these two with the first part, you will find that these two puzzles are essentially different from the first. In these two puzzles, the sequence of digits in the solution may be any without any restriction, whereas in the first puzzle, the digits had to be in decreasing sequence from 9 to 1.

Solution to the second puzzle: How many ways can you form the sum 99 with 9 digits from 1 to 9

The puzzle

Use digits 1 to 9 only once each to form numbers sum of which is 99. How many ways can you do it?

We already know,

1. There has to be at least 1 two digit number in the solution sum of 99.
2. The digits 9, 8 and 7 cannot take part as the tens digit in forming any two digit number in the solution sum.
3. With digit 6 as tens digit of a two digit number in solution sum, the result of addition 99 is possible.

With this knowledge, we will repeat the testing with 6 for being more clear about its success as the tens digit of the single two digit number.

For 6 as tens digit: taking 1 as its units digit to keep the sum of the rest to a minimum so that it doesn't exceed 99,

Sum with 61: $9+8+7+61+5+4+3+2=99$.

Let's examine the solution sum.

If we exchange any of the other digits, say 4, with 1, still the final sum remains unchanged. This is because,

Place value of 6 remains unchanged as 60 and place values of 1 and 4 also remain unchanged even though 4 now occupies the units digit place in 64 instead of 1. Their contributions in the solution sum remain unaltered.

Let's see the sum with 64,

Sum with 64: $9+8+7+64+5+3+2+1=99$.

So there are 8 possible combinations of sum 99 with 6 as the tens digit and each of the other 8 digits as the units digit.

Important Conclusion 1:

With only 1 two digit number in the solution sum, no digit other than 6 can be the tens digit of the single two digit number in the solution sum.

Verify yourself.

Now we will ask the first question in this puzzle solution.

Question 1: What is the inherent mechanism behind 6 to be the only digit that can be the tens digit of 1 two digit number in the solution sum?

Don't you feel curious to know the answer also?

In fact discovering this mechanism uncovers the most important KEY PATTERN using whih solving the rest of the puzzle will become straightforward.

The following figure shows visually how 6 fulfills its unique role of being the only digit that can be the tens digit in the single two digit number in the solution sum.

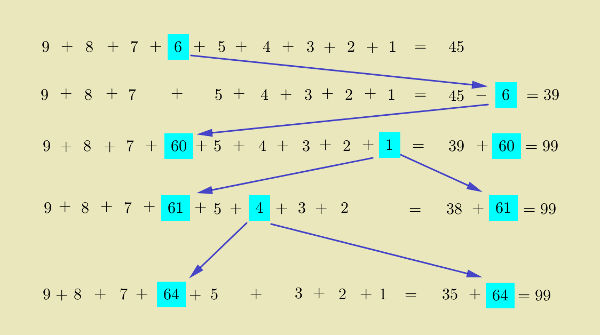
$\Rightarrow$ The figure first shows how the 9 individual digits sum up as 45.

$\Rightarrow$ From this sum, when 6 is taken out to be the tens digit of the single two digit number and added, its place values becomes 60 and the result of adding reduced sum of 39 of remaining 8 digits and 60 becomes 99.

$\Rightarrow$ Replace 0 of 60 by any of the 8 digits other than 6, and the sum still remains 99.

Effectively,

Dropping 6 from 9 digits and using this 6 as the tens digit with an additional zero makes the place value 6 as 60 which when added to the sum of remaining 8 digits 39, the final sum reaches 99. Replacing unit digit 0 of 60 with any of the 8 digits other than 6 doesn't change the final sum of 99.

This is the key pattern inherent in the problem that you have discovered by asking relevant questions, and analyzing the problem details using basic concept of place value.

As a consequence we can make the next important conclusion,

Conclusion 2: If any of the two digits among the nine sum up to 6, when the digits are used as tens digits of 2 numbers of two digit numbers with any other two digits as units digits, you would again get a sum of 99 of 2 two digit numbers thus formed and the rest 5 digits.

Test an example,

$9+7+6+5+48+3+21=99$, $4+2=6$ provides 60 and 8 and 1 are reassigned as units digits of the 2 two digit numbers 48 and 21.

You now realize that this will be true for any two digits among the 9 sum of which is 6.

Question 2: What are such combinations of two digits among the nine, sum of which is 6?

Answer 2: The combinations are, $4+2=6$ and $5+1=6$, only two.

Now we are on an assured path. The natural question asked is,

Question 3: How many solutions are possible with 2 numbers of two digit numbers in the solution sum?

Number of possible solutions with 2 numbers of two digit numbers in the solution sum of 99

Let's take the digits 1 and 5 for finding number of possible solutions with these two as tens digits.

Any two of the rest 7 digits can appear as the units digit of either 1 or 5 as the tens digit.

Distinct choice combinations of 2 out of 7 is $\displaystyle\frac{7\times{6}}{2}=21$.

For any of these combinations, each of the two digits can be placed as units digit of 1 as tens digit or with 5 as tens digit, that is, 2 possible solutions for each of the 21 possible two digit choices.

So with 1 and 5 as tens digits of 2 two digit numbers, there will be $21\times{2}=42$ possible solutions.

In the same way, for the other combination $4+2=6$, there will be 42 more possible solutions.

Conclusion 3: Total number of solutions possible with 2 two digit numbers is $42\times{2}=84$.

In the last step, we must answer the question,

Question 4: Can there be a combination of 3 digits summing up to 6 that would contribute to possible solutions? And if there is any, what will be the number of solutions possible for all such 3 numbers of two digit numbers in the solution sum?

Number of possible solutions with 3 numbers of two digit numbers in the solution sum of 99

For 3 numbers of two digit numbers, you can apply the same concept by answering the question,

Question 5: how many combinations of 3 digits among 9 digits sum up to 6?

Answer 5: There is only one such combination, $1+2+3=6$.

To form the 3 two digit numbers with digits 1, 2 and 3 as tens digits, three digits are to be chosen from the rest 6 digits to become the units digits of the three two digit numbers.

So the question we will ask is,

Question 6: How many combinations are possible for choosing 3 digits out of rest 6 digits?

Answer 6: It is the combination, 3 out of 6, $\displaystyle\frac{6\times{5}\times{4}}{3\times{2}}=20$.

Each of these 3 digit choices can be distributed as units digits among 1, 2 and 3 in a total of $3\times{2}=6$ number of ways.

So with three two digit numbers in the solution sum, possible solutions are $20\times{6}=120$ in number.

These are all the possibilities that are there with 1, 2 and 3 as tens digit in 3 two digit numbers in the solution sum.

Total number of solutions

With 1 two digit number in the solution sum, number of possible solutions is 8.

With 2 two digit numbers in the solution sum, number of possible solutions is 84.

With 3 two digit numbers in the solution sum, number of possible solutions is 120.

Total number of possible solutions is $8+84+120=212$, quite a large number.

Solution to the third puzzle: How many ways can you form the sum 99 with digits 1 to 9 and with minimum number of addition signs

The puzzle

Use digits 1 to 9 only once to form numbers, sum of which is 99. How many such combinations can you form using minimum number of addition signs?

Answering this Part 3 of the puzzle is now very easy.

The minimum number addition signs will be for minimum number of terms and the minimum number of terms will obviously occur with maximum number 3 of two digit numbers.

The number of terms will be 6 and addition signs 5, the minimum.

How many such possible solutions?

That is also easy. It will simply be the number of possible solutions with 3 two digit numbers in the solution sum.

The answer is 120.

This completes solution of all three parts of the puzzle.

End note

Though tedious, the steps give you the exact answer without making any assumptions and random trial.

This is systematic problem solving,

1. Systematic problem solving is not a single method that can be followed for solving all problems. It is a way adapting to the problem being solved and follow a series of assured steps to the solution.
2. The steps of systematic problem solving gradually narrow down the possibilities to arrive at the solution without fail.
3. It covers all aspects of the problem so that you know by the nature of the steps itself that the solution is exhaustive with all possibilities covered.
4. In systematic problem solving, on the way to the solution, key patterns must be discovered and used for subsequent steps.
5. A series of Question, analysis and answer create the steps to the solution, and,
6. Invariably, basic concepts form the foundation of the whole method.

In this case, Place value concept and the concept of permutation and combination in the form of arrangements provided the foundation.

Use of formulas

A tendency to use formulas stunts and more often kills the ability to solve problems inventively and systematically.

Happy problem solving.

---

Know how to solve difficult problems easily without wasting time on random attempts

Our ebook on puzzle solutions by innovative methods will show you just that.

Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving

(BUY from Apple books, Barnes & Noble, Rokuten Kobo, Vivlio, Angus & Robertson, Tolino, PayHip and others)

BUY the eBook Amazon Kindle version here, from Google Play here and Paperback here.

---

Puzzles you may enjoy

Easy to hard brain teasers with systematic solutions

Challenging brain teasers with solutions: Long list.

This will always be the most up-to-date full list with the brain teasers classified into categories that can be browsed separately.

You may also click on the category term link below to enjoy the brain teasers that are classified in the present category.

For example, if the category term link shown below is "Riddle", click on it to go through all the Riddles.

---