
Strategic approach and effective methods enable quick solution to Einstein riddle Who owns the fish
In this improved solution to Einstein's puzzle, learn how to find the answer to Einstein riddle who owns the fish confidently and systematically.
Preamble
Briefly,
five nationals of five different countries live in five differently colored houses, keep five different pets, drink five different fluids and smoke five different brands of cigarette.
In 20 minutes, analyze 15 given conditions and find answer to the question—who owns the fish?
The puzzle is the popularly known as Einstein’s puzzle or Einstein's riddle.
It is not easy, but not too difficult as well. You will enjoy solving the puzzle.
I have used terms for strategies, techniques and methods used in solving the puzzle, but also explained why the techniques are effective and how the methods are to be used.
Goal is—anyone of you should be able to understand how the problem is solved and learn to use the strategies and methods. It will be great if you can improve these. Expected outcome—your interest and involvement.
Let us start by first stating the problem and going through the systematic solution step by step.
Einstein's Riddle Who Owns the Fish: The 15 CONDITIONS
1 The Brit lives in the red house.
2 The Swede keeps dogs as pets.
3 The Dane drinks tea.
4 The green house is on the left of the white house.
5 The green house’s owner drinks coffee.
6 The person who smokes Pall Mall rears birds.
7 The owner of the yellow house smokes Dunhill.
8 The man living in the center house drinks milk.
9 The Norwegian lives in the first house.
10 The man who smokes Blends lives next to the one who keeps cats.
11 The man who keeps the horse lives next to the man who smokes Dunhill.
12 The owner who smokes Bluemasters drinks beer.
13 The German smokes Prince.
14 The Norwegian lives next to the blue house.
15 The man who smokes Blends has a neighbor who drinks water.
Einstein's Riddle Who Owns the Fish: QUESTION
Who keeps the fish?
Can you find out in 20 minutes? Well, that is the standard time limit for this puzzle. If you have time in your hands, go on till you solve it.
This is one of the most well-balanced puzzles I know of and I am sure you will enjoy solving it.
Remember,
The efforts to analyze and reach the solution is more important than the solution itself.
Solution to Einstein's riddle who owns the fish: Problem analysis and definition
The puzzle has six variables or dimensions—House: each with a specific position, Color of house, Occupant: each with a specific nationality, Pet, Drink choice, and Smoking choice. Each of these variables has five unique values.
As this should be a well-formed logic puzzle with a unique solution, we gather by a brief scan through the problem description, that, when fully assigned, there will finally be five unique combinations of values of six variables.
Values of the six variables (five for each variable) have to be assigned one-to-one. No single variable value can be assigned to two values of another variable.
For example, an occupant of a specific nationality living in a house of a fixed position of unique color, has a unique pet, drinks a unique drink and smokes a unique brand of cigarette.
Thus, the problem involves one-to-one assignment between six sets of variable values. The one-to-one assignment property makes the solution simpler.
A possible combination might be (but not necessarily be so),
The Swede living in blue house on the rightmost position smokes Dunhill, drinks beer and keeps dogs as pets.
At first glance, the logic puzzle may appear daunting unless the problem solver is naturally gifted or experienced.
Solution to Einstein’s riddle who owns the fish: Logic representation
We need to analyze the fifteen given logic statements to find out who owns the pet fish. These statements are also called logic statements, and this kind of problem, reasoning and logic analysis puzzle.
While we analyze the 15 logic statements one by one, we need to record the results at every step to aid analysis of the next logic statement. The results will get more enriched with each step and move towards the solution.
To record the results of logic analysis up to any stage, we’ll use the most compact logic representation of fully collapsed column logic table with five columns and five rows.
The houses identified by their positions form natural column labels with position embedded in each. The other five variable names form the row labels.
For example, the column labels will be from left to right—House 1, House 2, House 3, House 4 and House 5 with House 1 as the leftmost and the first house, and House 3 as the center house.
The row labels become then: Color of house, Occupant nationality, Pet, Drinks and Smokes.
Note: At first, you may think, person should be the column header. But each house having fixed relative position with each other, assigning house as the primary variable is more natural. Position of a house will not change but all else will change.
The column header variable house is the primary variable to which values of all the other 5 variables are assigned.
Choice of primary variable and forming the logic table correctly is important.
The empty logic table is shown in the figure. The job in hand is to fill up the 25 cells, or better still, find who owns the fish by analyzing the 15 logic statements.

Solution to the Einstein's riddle who owns the fish: Objectives
At first, it seems we need to find all the five unique combinations of six variables filling up all 25 cells of the logic table. But on review of the problem, we perceive we need just to find who owns the fish, even if a few cells stay empty. This is then our main goal.
In this solution, we will try to find the answer in a few steps, quick and easy. This is our methodological goal.
To achieve these objectives, we will use powerful strategies, patterns, and methods. These are formed by solving many logic puzzles and Sudoku problems and are based on common sense reasoning. I will explain the mechanism of each.
Solution to Einstein's riddle who owns the fish: Logic analysis stage 1
Use of Direct assignment first strategy and link search technique.
While solving this type of problem, we need to form a strategy of processing the logic statements. Going serially from the first to the second and so on may end up in hopeless confusion.
First strategy: Direct assignment first
The most important strategy at the start is to process those statements that make certain and distinct assignments to any of the cells. We call this strategy as the direct assignment first strategy.
Note: This makes sense, as a statement that states with certainty that a variable value belongs to a specific single cell must get the highest priority of processing. This reduces the uncertainty of the whole logic table.
In this problem, such a statement must have mention of a house by its position.
A specific national lives in a house at a specific position. Except color of the house, all the other three variables, Pet, Drinks and Smokes, are attributes of the national. So preference will be given to a statement in which a specific national is involved.
With these decisions, the “Statement 9. The Norwegian lives in the first house” is chosen as the first statement to analyze. This puts the national Norwegian in House 1, and so the corresponding cell in the table is filled.
Second strategy: Link search technique
Any statement that refers to the already assigned national and additionally helps to make another certain assignment is chosen next. This assignment by link or reference technique is extremely valuable and is used as soon as we get certain of a new value in the table. This is called link search technique.
So, “Statement 14. The Norwegian lives next to the blue house” is processed second putting color blue to the House 2 because of no house on the left of Norwegian’s first house. Elementary logic analysis used. It forms one of the main foundations of logic puzzle solving.
Third strategy: Repeat direct assignment first and link search
When we get “blue” as the color of the second house, we search for any statement that refers to “blue” and gives us another certain assignment. This method we follow as part of link search technique. Here, though, we don’t have such a statement. Link search chain ends here.
But what about direct assignment statements? Is there any more left? So we repeat the steps.
This is repeating direct assignment first and then use link search strategy. This should produce maximum certain assignments in this first stage.
Searching for the second direct assignment, we locate “Statement 8. The man living in the center house drinks milk”, that enables us to assign milk in the Drinks cell below the House 3 column.
This ends the first stage and the logic table result is shown.

Solution to Einstein's riddle who owns the fish: Logic analysis stage 2
Use Bonded member structures on same variable and with highest potential.
With no further reference to already assigned values “Norwegian”, “milk” or “blue” and no more direct assignment statements available, we have to adopt a new strategy based on a new pattern of temporary bonded member structure.
Such structures can be formed on same variable values or values of different variables. Preference is for the first type of temporary bonded member structure on same variable values.
Fourth strategy and pattern
When a logic statement refers to two (or more than two) values of the same variable, and mentions positional relation of the values (column-wise), we get a temporary bonded member structure on same variable.
Mark that the related values in a temporary bonded member structure of this type must be of same variable, and in this case must belong to the same row.
With more than one such statement forming temporary bonded member structures, the statement that spans largest number of bonded cells of a row is selected to be of highest potential.
In our problem, we identify "Statement 4. The green house is on the left of the white house", as the only statement forming a temporary bonded member structure on color of house—green on the left of white. Green house is related to the white house by position.
By elementary logic analysis, we conclude,
Colors green on the left of white can only be assigned to House 3-House 4 or House 4-House 5, as the first two houses are already blocked.
The condition of only two possible values of two variables is two-degree uncertainty. Because of only two possibilities, this has a high probability of a later statement removing one possibility by conflict to convert the remaining one as a certainty. This is a valuable condition and aids quick solution.
The following state of logic table shows how we record the temporary bonded member structure.
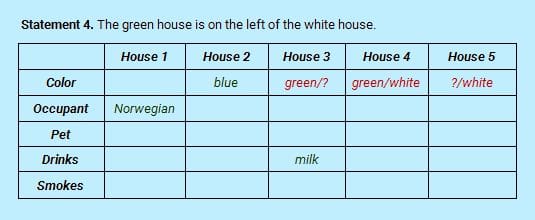
With possibilities of green and white constrained, now we search for a statement that refers to either green or white as well as creates new certain assignments. This is use of link search technique.
Such a statement is “Statement 5. The green house’s owner drinks coffee”.
It conflicts with Drinks value of House 3 for green color and thus eliminates this possibility.
Green color and Drinks coffee combination is left for the House 4 with certainty. Color white automatically is assigned to House 5.
At one go, you get three certain assignments. The result of processing the Statement 5 is shown.

We could have processed the 4th and 5th statements together, but for showing the mechanism of the combined strategy we have kept the two steps separately.
Solution to Einstein's riddle who owns the fish: Logic analysis stage 3
Focus on most-filled row and elementary logic analysis.
We applied the earlier strategies during the initial stages when the logic table was nearly empty. But as the logic table now is well-filled and also the earlier strategies can no longer be used, we look for new and easier opportunities.
Fifth strategy: Focus on the most-filled row or column and search for conflicts
By this strategy, we look for conflicts resulting in unambiguous assignments.
It makes sense that,
A row or column that is filled up with maximum number of cell values (or having the least number of empty cells) will have the highest potential for a statement creating a certain assignment.
The target row at this stage is the row of house color, and as expected, the “Statement 1. The Brit lives in the red house” gives us the unambiguous assignment by conflict.
The elementary logic analysis is straightforward.
With colors of House 1 and House 3 left to be known, and the Norwegian living in House 1,
The red-colored house in which the Brit lives must be the House 3. Certain assignment is achieved by conflict in nationality (the Norwegian lives in House 1 blocking it for the Brit) and color pair of properties.
Sixth strategy and pattern: certain assignment by exclusion
This is a very favorable condition when out of a set of values for a variable, only one value is left to be assigned to one empty cell left for the variable. The last value automatically gets assigned to this remaining cell.
In our problem by this strategy,
Yellow color is automatically assigned to House 1.
Now applying link search, “Statement 7. The owner of the yellow house smokes Dunhill” is chosen as it links already assigned color yellow with Smokes variable value.
In the same way, “Statement 11. The man who keeps the horse lives next to the man who smokes Dunhill”, is processed next, assigning horse as pet against House 2.
The Statement 7 and then Statement 11 together give us—a chained link search.
The logic table at this stage is shown.
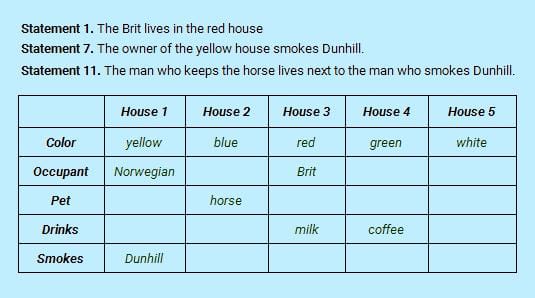
At this stage, let’s stop for a moment and take stock.
We have processed more than half of the 15 logic statements filling up less than half of the 25 logic cells, but also exhausted possible use of patterns and techniques used till now. Verify correctness of the conclusion.
To break the bottleneck and continue to fill the logic table, we must use a new strategy and pattern with its associated method.
Solution to Einstein's riddle who owns the fish: Logic analysis stage 4
Breakthrough by Temporary bonded member structure on two variable values, use of multiple statements, Possibilities, and Cycle.
Earlier we hinted—when no easy avenue towards solution is visible, form a temporary bonded member structure. Now also we do that.
We form temporary bonded member structures not on same variable values (because no statement is left to do that), but on values of different variables.
We repeat the most potent strategy in solving difficult reasoning puzzles,
When no easier path towards the solution is available, form and use temporary bonded member structures.
With this knowledge, we pick up together “Statement 3. The Dane drinks tea” and “Statement 12. The owner who smokes Bluemasters drinks beer”, to check the columns where we can place these two pairs of values of different variables.
Promptly, we find that the two temporary bonded member structures, Dane-tea, and Bluemasters-beer can be placed in House 2 and House 5 columns or vice versa.
These create two possibilities with two-degree uncertainty and we cannot write this information on the main logic table easily. So we combine these two results and create—two Possible scenarios or Possibilities (multiple logic table possibilities). The information is recorded separately from the main table.
Top part of the following figure is these two possibilities where, for brevity we have not shown the main logic table.

As these are two different possibilities, we cannot merge any of these two with the main logic table. Instead, we keep the possibilities separate from the main table.
Rest of the statements are processed with the goal of proving one of the two possibilities as invalid and merging the valid one with the main table.
In solving any complicated reasoning puzzle, you may have to adopt this advanced strategy.
The structure and role of Cycle
When we analyze the two possibilities, our attention is drawn naturally to the Drinks values. We find a wonderful new structure waiting to be formed in this Drinks row.
See that the two values “tea-beer” can be placed only in two cells of the same Drinks row under House 2 or House 5. This is a temporary bonded member structure of two-degree uncertainty on same variable but with mutually reverse positional relationship.
If House 2 occupant drinks “tea”, House 5 occupant must drink “beer”, and vice versa.
This powerful new structure is a Cycle. The two values of the same variable cycle through the two cells and effectively block these two cells from placement of any other Drinks value. This cycle is represented in the lower part of the above figure.
The cycle blocking two Drinks values and two Drinks row cells, the remaining Drink “water” gets automatically assigned to occupant of House 1 by exclusion.
Applying link reference, we analyze next “Statement 15. The man who smokes Blends has a neighbor who drinks water”, and assign “Blends” to occupant of House 2.
This invalidates the Possibility 2 and “Bluemasters” with “beer” are assigned to occupant of House 5 and “Dane” with his drink “tea” are assigned to House 2.
This is a critical step of analysis and you should check for yourself till fully satisfied.
The critical barrier is broken through by the combined use of temporary bonded member structure on two variables, creation of two Possibilities and finally a Cycle. This is the most important breakthrough in the puzzle.
From this point on, the rest are all easy pickings and even without writing the assignments you can tell the correct answer. Still, for ease of explanation, we will go ahead with the rest of the solution.
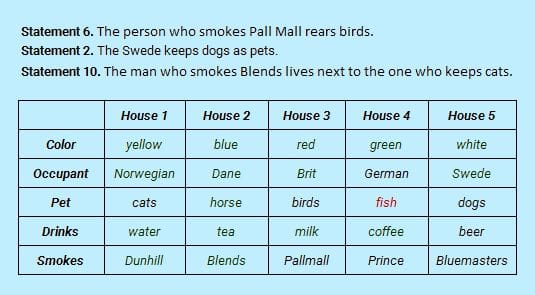
The first assignment now is straightforward—with Smokes row nearly full, “Statement 13. The German smokes Prince” is analyzed next for certain assignment by conflict with Smokes value Bluemasters.
The state of the logic table is shown below along with the four statements that we processed after the earlier stage.

Solution to Einstein's riddle who owns the fish: Logic analysis final stage
First by exclusion on Smokes row, we select “Statement 6. The person who smokes Pall Mall rears birds”, then by direct assignment “Statement 2. The Swede keeps dogs as pets”, and last by link reference, “Statement 10. The man who smokes Blends lives next to the one who keeps cats”.
The assignments leave Fish for the German.
The final state of logic table is shown.
End note
Patterns and systematic methods do take away the mystery of the puzzle somewhat. But, it improves the ability to identify, form and use new patterns and methods in unraveling mysteries of new problems.
Know how to solve difficult problems easily without wasting time on random attempts
Our ebook on puzzle solutions by innovative methods will show you just that.
Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving
BUY the eBook Amazon Kindle version here, from Google Play here and Paperback here.
Second book on Innovative Solutions to Matchstick Puzzles from Suresolv

BUY Creative Matchstick Puzzles Innovative Solutions eBook Amazon Kindle version
BUY the paperback here.
Puzzles you may enjoy
Easy to hard brain teasers with systematic solutions
Challenging brain teasers with solutions: Long list.
This will always be the most up-to-date full list with the brain teasers classified into categories that can be browsed separately.
You may also click on the category term link below to enjoy the brain teasers that are classified in the present category.
For example, if the category term link shown below is "Riddle", click on it to go through all the Riddles.
