
Move 3 matches to make 3 squares - Matchstick puzzle on Tic Tac Toe
Move 3 matches to make 3 squares from the Tic Tac Toe matchstick figure.

How many unique solutions can you find?
Recommended time to solve: 5 minutes.
Give it a try. It will surely be fun.
Hint: Use your analytical reasoning instead of random trial and error.
We’ll solve the puzzle step by step by analyzing the puzzle structure and making conclusions based on common stick constraint and a series of questions, analysis and answers.
Solution to Move 3 matches to make 3 squares Tic Tac Toe Matchstick puzzle: Structural analysis, Common stick analysis, Chain of reasoning by Question analysis answer
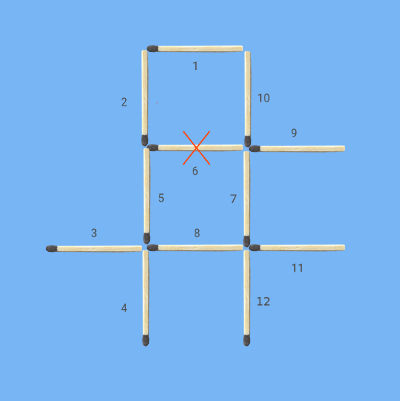
The following is the Tic Tac Toe matchstick puzzle figure with each stick numbered uniquely. This will help us explain.

First step in solving any matchstick puzzle is to count number of sticks in the puzzle figure. It is exactly 12.
Question 1: How many matchsticks do you require making 1 square?
Answer: It is 4.
Question 2: How many sticks would you need to make 3 INDEPENDENT squares.
Answer: 2: To make 3 independent squares you need exactly 12 matchsticks that you already have.
As you know that if there were a single stick common between two squares need for sticks would have reduced by 1 to 11, you can make your first conclusion. This is a key conclusion or key pattern identification based on the common stick concept.
Conclusion 1: The three squares in the solution figure won’t have any common stick between any two of them.
Note: This is what we call key pattern identification and precise requirement specification for the final solution. Subsequent analysis and decisions will follow from this result.
Chain of reasoning based on common stick constraint and Identification of sticks to move
Look at the puzzle figure and take stock.
Observation: There are four nearly complete squares in the tic-tac-toe. Each has three sides already in place (three times four makes up the 12 sticks). Only 1 stick is required to close the fourth side and complete a square in each.
These are,
I: Sticks 1, 5, 3.
II: Sticks 4, 8, 12.
III: Sticks 11, 7, 9.
IV: Sticks 10, 6, 2.
Conclusion 2: Some of these four one side only open nearly complete squares must be completed to make the final solution figure. This is an obvious conclusion.
Now ask yourself the question,
Question 3: What would be the situation if any of these nearly complete squares is completed?
Just assume, the square with sides 10, 6, 2 is completed by moving stick 1. Any problem you observe?
Answer 3: Yes there will be a serious problem.
It will create a common stick 6 with the existing central square made up of sticks 5, 6, 7, 8.
An example is shown for making the consequence clear. This is not trial and error. This is the well-used and highly valuable management technique of Consequence analysis.
That’s why you have to make the third important conclusion,
Conclusion 3: To make the solution you want, the central square MUST be destroyed by selecting one or more than one stick among 5, 6, 7, 8 for moving.
As all the four nearly complete squares are STRUCTURALLY EQUIVALENT, you may choose any of the four.
Action 1: So you choose stick 5 with full confidence that this must give you a solution. And move it straightaway to complete one of three remaining nearly complete squares, say square with three sides 11, 7, 9.
The result of the action is shown below.
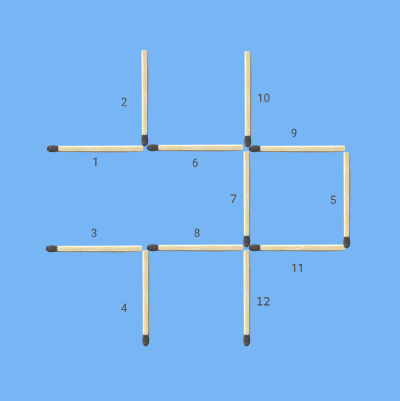
Well, well, well. You have got the solution in your pocket with this single confident action.
The two sticks 1 and 3 are hanging, ready to be moved to complete the other two squares, the square with three sides 10, 6, 2 and the square with three sides 4, 8, and 12.
Following results from these actions. We have kept the original sticks that we have moved, but made them faded to give you a very clear idea on how you have created the solution figure from the starting figure.

Consider that you could have selected any of the other three one-side-open-three-stick components to form three perfect squares. But the result would have been the same if you would just rotate the figures suitably.
So we conclude,
These three other solutions would be rotationally the same with the solution you have created. That means, the solution is rotationally unique.
You may try for any other solution figure. You won’t get any more as you know your reasoning has been bullet proof.
End note
We have approached the problem systematically and analytically, and not in any random way. This is what we call the systematic approach to problem solving.
Generally, the systematic approach to problem solving depends heavily on identification of key patterns, creation of effective methods and deductive reasoning to move towards the solution without any confusion and in a minimum number of steps, if possible.
This is the systematic problem solving.
Last, to solve matchstick puzzles you don’t need to know maths or any other subject—you just have to identify key patterns and use your inherent analytical reasoning skills to home in to the solution with assurance and speed.
Know how to solve difficult problems easily without wasting time on random attempts
Our ebook on puzzle solutions by innovative methods will show you just that.
Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving
BUY the eBook Amazon Kindle version here, from Google Play here and Paperback here.
Second book on Innovative Solutions to Matchstick Puzzles from Suresolv

BUY Creative Matchstick Puzzles Innovative Solutions eBook Amazon Kindle version
BUY the paperback here.
Puzzles you may enjoy
Easy to hard brain teasers with systematic solutions
Challenging brain teasers with solutions: Long list.
This will always be the most up-to-date full list with the brain teasers classified into categories that can be browsed separately.
You may also click on the category term link below to enjoy the brain teasers that are classified in the present category.
For example, if the category term link shown below is "Riddle", click on it to go through all the Riddles.
