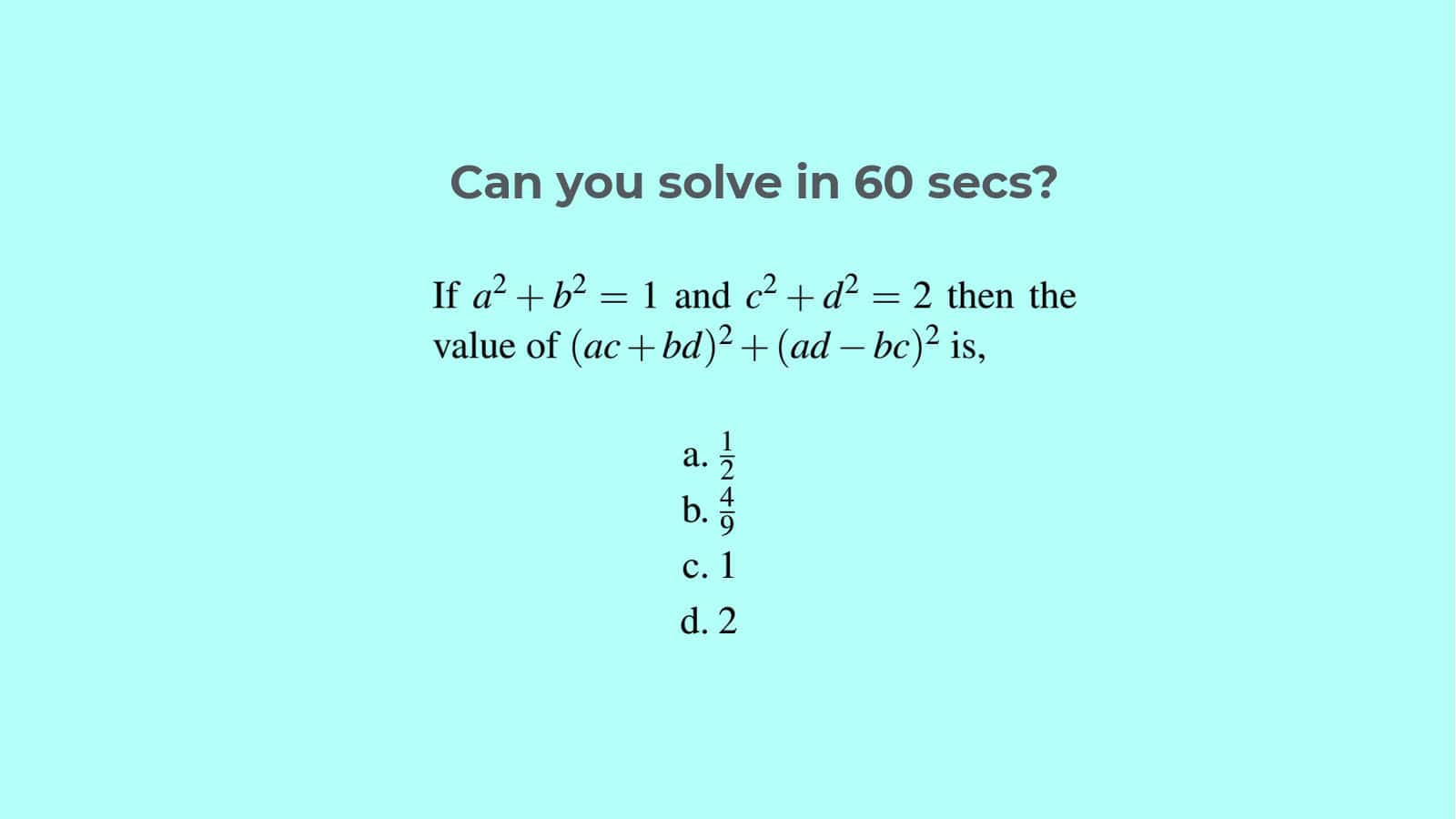
Problem solving techniques to solve the difficult algebra problems in a few simple steps
A few hard algebra problems are solved quickly in a few simple steps. How to solve a hard algebra problem easily by problem solving techniques explained.
Sections are,
- A few words on hard algebra problems.
- Frequently used algebraic formulas and concepts (or algebraic identities): Needed in solving practically any hard algebra problem
- Quick solution to a few chosen hard algebra problems: Problem solving techniques used in identifying key pattern for breakthrough and quick solution in a few steps. Explained step by step.
A few words on hard algebra problems
Basic Algebra is based on a small set of concepts. But use of abstract symbolic variables poses first level of difficulty in understanding.
In addition, based on the small number of building blocks of concepts, Algebraic expressions may be made to appear very complex posing the second level of difficulty in understanding.
That's why hard algebra problems are often used in most competitive exams worldwide to test the skills of pattern identification and use of appropriate concepts and techniques that are basic skills in problem solving in general.
Lastly recognition of useful patterns in complex expressions is an essential skill in solving hard Algebra problems.
As not everyone is adept in recognizing useful patterns that is not so visible, the need of key pattern recognition forms the third level of difficulty in algebra problem solving.
If you know the frequently algebra problem solving formulas and concepts, you decide to skip the next section and move straight to solving of chosen problems. To skip next section, click here.
Basic and Rich Algebraic Concepts - Frequently used algebraic formulas and algebra problem solving concepts
The basic operations involved in Algebra are none other than all the basic arithmetic operations, but on abstract symbolic variables and expressions, not on numbers.
The more important relationships in Algebra forming the basic concept layer of Algebra are the following.
$(a + b)^2 = a^2 + 2ab + b^2$, in the form of square of sum of two variables.
$(a - b)^2 = a^2 - 2ab + b^2$, negative counterpart of the sum of two variables.
$a^2 - b^2 = (a + b)(a - b)$, this is one of the most useful algebraic relationships.
$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$, in the form of cube of sum of two variables.
$(a + b)^3 = a^3 + b^3 + 3ab(a + b)$, this cube form is used frequently and it is better to remember it as a basic concept.
$(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$, negative counterpart of cube of sum of two variables.
$(a - b)^3 = a^3 - b^3 - 3ab(a - b)$, which again is useful.
Derived from the cubes of sums we get the next set of basic relationships that are frequently used.
$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$, a very useful relationship to be remembered and used in the right places.
$a^3 - b^3 = (a - b)(a^2 + ab + b^2)$, negative counterpart and equally useful.
Similarly it pays to know the similar expressions in three variables.
$(a + b + c)^2 $
$\hspace{10mm} = a^2 + b^2 + c^2 + 2(ab + bc + ca)$,
$(a + b + c)^3 $
$\hspace{10mm} = a^3 + b^3 + c^3 + 3(a + b)(b + c)(c +a)$,
$a^3 + b^3 + c^3 - 3abc $
$\hspace{10mm} = (a + b + c) \times{}$
$\hspace{20mm} (a^2 + b^2 + c^2 - ab - bc - ca)$
Rich algebra problem solving concept
Under this category we would put the result of three variable zero sum principle.
If $a + b + c = 0$, then $a^3 + b^3 + c^3 = 3abc$ which is a very useful concept.
Recommendation: Except the relations in two variables and the rich concept you may not memorize the relations in three variables. That would create extra memory load on you compared to its gains. It is just simple cost-benefit analysis.
Let use delve into our problem solving activities without any further delay.
Quick solution of chosen hard algebra problems in a few steps
Hard Algebra Problem 1.
If $a^2 + b^2 = 1$ and $c^2 + d^2 = 2$ then the value of $(ac + bd)^2 + (ad - bc)^2$ is,
- $\displaystyle\frac{1}{2}$
- $\displaystyle\frac{4}{9}$
- $1$
- $2$
Solution:
First stage Problem analysis:
At first glance the expressions though seem to be a bit complex involving as many as 4 variables, on closer examination of the end state, or the expression to be evaluated, we find a promising clue to the solution.
First clue:
If we imagine both the squares of sums expanded, the middle terms in each three term expression are transformed to the equal value $2abcd$ and fortunately, in opposite signs. These will then be cancelled out and the problem state will be considerably simplified.
Let us put this thought to practice calling the target expression as $E$ for convenience,
$E= (ac + bd)^2 + (ad - bc)^2 $
$\hspace{5mm} = (a^2c^2 + 2abcd + b^2d^2) $
$\hspace{10mm} + (a^2d^2 - 2abcd + b^2c^2)$,
$ \hspace{5mm} = (a^2c^2 + b^2d^2) + (a^2d^2 + b^2c^2)$
Second stage problem analysis:
Now we look at the four terms left out and examine this expression against the given expressions looking for the presence of expressions $a^2 + b^2$ and $c^2 + d^2$ in the current simplified target expression.
We always go through this comparison by following the End State Analysis Approach at every stage of simplification and progress towards solution. At this stage the four term simplified expression is our end state expression.
With this closer examination looking for specific patterns, invariably we find the second clue.
Second clue:
In the first terms of the two term expressions, we find $a^2$ common as well as $b^2$ common in the last two terms. Thus we apply our Principle of collection of friendly terms putting our promising information discovery to practice,
$E = (a^2c^2 + b^2d^2) + (a^2d^2 + b^2c^2)$
$\hspace{5mm} = (a^2c^2 + a^2d^2) + (b^2c^2 + b^2d^2)$
$\hspace{5mm} = a^2(c^2 + d^2) + b^2(c^2 + d^2)$
The given expressions have magically appeared and are waiting to be substituted with their values,
$E = 2(a^2 + b^2) = 2$
Answer: Option d: 2.
Key concepts used:
By the use of End State Analysis on the target end state expression discovery of $2abcd$ cancelling out when the two squares of sums are expanded.
Again using End State Analysis on the simplified four term expression, this time we look for the presence of given expressions $a^2 + b^2$ and $c^2 + d^2$ in the four term expression.
When you search for something that you know, chances are high that you would find it. We find thus the common terms of $a^2$ in first terms and common $b^2$ in second terms of the two sums of squares in the simplified target expression.
Now we apply Principle of collection of friendly terms and actually see the given sum of squares expressions appear in the target expression. Solution took one step more.
Summary of deductive steps:
$E= (ac + bd)^2 + (ad - bc)^2 $
$\hspace{5mm} = (a^2c^2 + 2abcd + b^2d^2) $
$\hspace{10mm} + (a^2d^2 - 2abcd + b^2c^2)$
$ \hspace{5mm} = (a^2c^2 + b^2d^2) + (a^2d^2 + b^2c^2)$
$ \hspace{5mm} = (a^2c^2 + a^2d^2) + (b^2c^2 + b^2d^2 )$
$ \hspace{5mm} = a^2(c^2 + d^2) + b^2(c^2 + d^2)$
$ \hspace{5mm} = 2(a^2 + b^2)$, substituting value of $c^2 + d^2$,
$ \hspace{5mm} = 2$
Aside:
When we put the deduction steps together, these form only a few simple but intelligently analyzed steps. In fact, when we face this question in a competitive test under time pressure we do not actually deduce these steps on paper. We do it all in mind in a few tens of seconds.
This would be possible certainly if we are aware and experienced in using the right problem solving strategies and identifying useful patterns at all stages of the deduction process.
The detailed explanation embodies the thinking involved in solving the problem. This we call our Deductive Reasoning that is much more than usual Reasoning.
Hard Algebra Problem 2.
If $6^{-z} = 2^x = 3^y$ then the value of $\displaystyle\frac{1}{x} + \displaystyle\frac{1}{y} + \displaystyle\frac{1}{z}$ is,
- 1
- 0
- $-\frac{1}{2}$
- $\frac{3}{2}$
Problem analysis
The target expression is very symmetric in $x$, $y$ and $z$, and all of 2, 3 and 6 are eliminated.
First conclusion:
To solve this problem, we must transform the bases in such a way as to equalize the transformed base values on two sides of an equation using our Base equalization technique.
As the bases become equal such as in $a^p = a^q$ we can conclude mathematically that $p = q$ where $p$ and $q$ may themselves be full-fledged expressions in some other variables.
In our problem, $p$, $q$ both will be in terms of $x$, $y$ and $z$ and the base $a$ will be in terms of either 2 or 3 or something common.
Now the main question is how to equalize the bases!
Rich concept on Chained equations
The three expressions chained together by two equal signs form what we call a Chained equation. In such an equation there might have been any number of expressions with number of equal signs one less than the number of expressions.
Usually we feel a little uncomfortable regarding how to break up the chained equation in the form of individual stand-alone equations and in what sequence.
The rich concept that usually produces elegant solutions under these conditions is to extend the chain by putting another equal sign and appending to the sign, an artificial variable, say, $q$. By this technique we become free to form an equality expression from every expression present in the chain, and easily manipulate these equations to eliminate $q$ and any other variables as needed.
This techniques eases the deductions considerably. We would see now how this happens.
$6^{-z} = 2^x = 3^y$,
Or, $6^{-z} = 2^x = 3^y = q$.
From this, we form first the simplest equation (2 is less than 3, though the simplicity is psychological only),
$2^x = q$.
Now we should be able to see the pattern and discover the crucial approach towards successful solution. We remember that in the target expression we had $\displaystyle\frac{1}{x}$. This is enough for us to transform this equation in 2 as,
$2^x = q$,
Or, $2 = q^{\frac{1}{x}}$.
By this not only we get a power in inverse of $x$ as we wanted but also made 2 free from any variable power.
Similarly for expression in 3 we get,
$3^y = q$,
Or, $3 = q^{\frac{1}{y}}$, and for the expression in 6,
$6^{-z} = q$.
Or, $6 = q^{\frac{1}{-z}}$.
All of the bases, 2, 3 and 6 have become free now for combining them,
$2\times{3} = q^{\frac{1}{x} + \frac{1}{y}}$,
Or, $6 = q^{\frac{1}{x} + \frac{1}{y}} = q^{\frac{1}{-z}}$.
Thus, we have our solution. As the base $q$ is equalized, the powers must be equal,
$\displaystyle\frac{1}{x} + \displaystyle\frac{1}{y} = \displaystyle\frac{1}{-z}$,
Or, $\displaystyle\frac{1}{x} + \displaystyle\frac{1}{y} + \displaystyle\frac{1}{z} = 0$,
Neat, isn't it?
Answer: Option b: 0.
Key concepts used:
At the very outset, deciding that Base equalization technique will have to be used for equating the powers as expressions in $x$, $y$ and $z$. The question of how to do this was easily resolved by using the Chained equation treatment technique of introducing an artificial neutral equality variable $q$ and noting also that $6 = 2\times{3}$. That is Pattern recognition. The procedure all along was helped by End state analysis.
Forming equations in 2, 3 and 6 with unity powers and transforming the powers of $q$ thereby finally produced the crucial equality expression by multiplying the expression of 2 and 3 and equating with that of 6.
Summary of deductive steps:
$6^{-z} = 2^x = 3^y$,
Or, $6^{-z} = 2^x = 3^y = q$. We transform first, expression in 2,
$2^x = q$,
Or, $2 = q^{\frac{1}{x}}$. Similarly,
$3 = q^{\frac{1}{y}}$, and
$6 = q^{\frac{1}{-z}}$.
Multiplying expression in 2 by 3 and equating with value of 6 in the RHS of expression in 6,
$2\times{3} = q^{\frac{1}{x} + \frac{1}{y}}$,
Or, $6 = q^{\frac{1}{x} + \frac{1}{y}} = q^{\frac{1}{-z}}$.
Equating the powers as the base $q$ is same on both sides of the equations,
$\displaystyle\frac{1}{x} + \displaystyle\frac{1}{y} = \displaystyle\frac{1}{-z}$,
Or, $\displaystyle\frac{1}{x} + \displaystyle\frac{1}{y} + \displaystyle\frac{1}{z} = 0$.
Aside:
Same as in the previous example, we put the deduction steps together to form only a few simple but intelligently analyzed steps. Again, when we face this question in a competitive test under time pressure we won't have to actually deduce these steps on paper. We would do it all in mind in a few tens of seconds.
The detailed explanation we call as Deductive Reasoning that is much more than usual Reasoning.
Here we have told you about the basic and rich concepts in Algebra and also about how to to solve a few selected types of Algebra problems in a few simple steps by using problem solving strategies, principles and techniques and of course with the help of deductive reasoning.
The list of Difficult algebra problem solving in a few steps quickly is available at, Quick algebra.
Guided help on Algebra in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Algebra in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Algebra in Suresolv and is up-to-date.