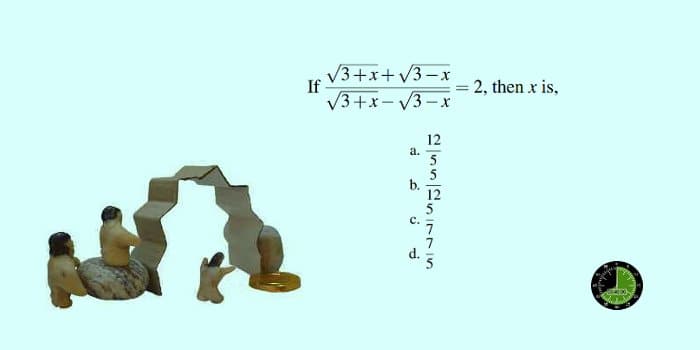
The problem solving method that you choose should be elegant as well as fully compatible with your skill-set
Algebraic rich concepts and techniques along with general problem solving strategies enable elegant solution to the difficult SSL CGL Algebra problem in this eleventh session of algebra problem solving in a few simple steps. This time our emphasis has been analyzing the two feasible solutions of the chosen problem, one of which uses rich algebraic technique and the other classical methods. Incidentally in this case, if executed carefully, both methods will reach you to the solution nearly equally fast depending on your skill-set and comfort level with the approaches.
Students in schools or in competitive tests such as SSC CGL generally find Algebra problems difficult.
We'll not repeat the usual reasons behind the difficulties faced by students in solving Algebra problems and the set of basic and rich concepts that are invaluable in reaching elegant solutions for seemingly difficult Algebra problems.
The list of Difficult algebra problem solving in a few steps quickly is available at, Quick algebra.
In this session also we will show you two methods of solution both nearly equally fast and we will analyze various aspects of the two methods.
How much confidence do you have on the method of solving the problem that you have chosen
When you start solving a not so easy algebra problem under time pressure in a major competitive exam such as SSC CGL, the most important factor working towards success will undoubtedly be the problem solving strategy you will adopt after brief analysis of the problem.
If you choose to take up a solution path on which you don't have full confidence, you may falter on the way and lose valuable time. You must know that in such cutting edge front-line tests as SSC CGL,
Every second saved contributes towards your ultimate success.
This is why after brief analysis of the problem, you should always choose a strategy of problem solving, that is efficient in terms of number of steps and time taken as well as with which you are fully confident. Both aspects are important,
The problem solving strategy should be efficient and elegant and at the same time it should be most familiar to you with highest assurance level.
This happens only when the method that you choose is fully compatible with your skill-set.
This point is important,
you must choose the problem solving method which is not only elegant but also you like most, whatever be the general advise.
Our recommendation is,
- In exam-hall decision making you must be fast, sure and confident with no hesitation at all at any point, including choice of problem solving strategy for each problem.
- In the process, you might make one or two mistakes, but make those few mistakes quickly and confidently to take up a new problem without any delay.
- Better it is to leave a few problems if you feel any bit unsure, because in any case you are not expected to solve all MCQ based questions accurately in any test, and
- Best it is to choose the problem solving strategy which will surely lead you to the solution in a few steps. This is what we call Assured Solution in a few steps.
Speed is certainly important, but degree of confidence in a problem solving strategy is no less important.
In this session while solving the problem we have chosen this time,
We will show you two methods to solution, both elegant and fast. In one we will use, the rich algebraic concept of componendo dividendo technique applied twice, which is unusual. The other method surprisingly is the classical deductive method. While we compare the two, you can assess yourself the pros and cons of the methods from your own point of view.
It is of utmost importance that you follow your own inclinations with acquired wisdom.
We urge you to try solving the problem on your own and note the time you took before going through our solution processes.
You may watch the video of this solution below,
Chosen Problem.
If $\displaystyle\frac{\sqrt{3+x} + \sqrt{3-x}}{\sqrt{3+x} - \sqrt{3-x}}=2$, then $x$ is,
- $\displaystyle\frac{12}{5}$
- $\displaystyle\frac{5}{12}$
- $\displaystyle\frac{5}{7}$
- $\displaystyle\frac{7}{5}$
Solution - Problem analysis:
Given is an equation in single variable $x$ involving square root and desired is the value of $x$. Only problem is that the given equation is not a simple linear equation.
One approach may be to transpose the denominator to the other side of the equation and find a relation of two unique elements, $\sqrt{3 + x}$ and $\sqrt{3 - x}$, raise both sides to square and then solve for $x$. We will explore this direct approach later.
On the other hand, whenever we find such an algebraic fraction as of the form, $\displaystyle\frac{a+b}{a-b}=p$, usually we quickly explore the usefulness of applying the time-tested technique of componendo-dividendo. As the elegant solution we will take this approach for this problem.
Componendo-dividendo technique
Problem: If $\displaystyle\frac{a + b}{a-b} = 3$ find the ratio of $a$ and $b$.
Solution:
Adding 1 to both sides of the given equation,
$\displaystyle\frac{2a}{a-b} = 3 + 1$
In the second step subtract 1 from both sides of the given expression,
$\displaystyle\frac{2b}{a-b} = 3 -1$.
Now divide the first equation by the second so that the denominator $a-b$ and 2 in the numerator are canceled out,
$\displaystyle\frac{a}{b} = 4 \div {2} = 2$.
Note: if $a-b$ were in the numerator here, the result would have been,
$-\displaystyle\frac{a}{b} = 4 \div {2} = 2$.
This is a very easy to execute technique and usually produces the fastest result avoiding expansion of the terms on both sides.
Solution - Problem solving execution
$\displaystyle\frac{\sqrt{3+x} + \sqrt{3-x}}{\sqrt{3+x} - \sqrt{3-x}}=2$,
Or applying componendo-dividendo technique on two sides of the equation we have,
$\displaystyle\frac{\sqrt{3+x}}{\sqrt{3-x}}=\frac{2+1}{2-1} =3$,
Or squaring both sides,
$\displaystyle\frac{3+x}{3-x} = 9$
Again we find the LHS to be nicely suitable for applying componendo-dividendo technique. Thus we get,
$\displaystyle\frac{3}{x} = \frac{10}{8}$
Or, $x = \displaystyle\frac{24}{10}=\frac{12}{5}$.
Answer: Option a : $\displaystyle\frac{12}{5}$.
Alternative to applying componendo dividendo the second time
Before applying the componendo-dividendo technique the second time we had,
$\displaystyle\frac{3+x}{3-x} = 9$.
Directly we could have simplified,
$3+x=9(3-x)= 27 - 9x$,
Or, $10x = 24$,
Or, $x=\displaystyle\frac{12}{5}$.
Though this looks simpler we still would prefer to use the componendo-dividendo approach as it can be executed mentally faster and more accurately if you are used to the technique.
Key concepts used: Using componendo-dividendo technique twice to reach the solution in a few steps. This solution can be reached mentally.
Second solution
Though the given expression conforms to the application of componendo-dividendo technique nicely, we still look into the nature of the terms closely to find the second solution of direct evaluation of $x$ from the given expression by classic method that is no less inviting.
This is direct variable evaluation technique and we classify this as a classical approach. Though it is usually suited for non-MCQ based exams, you need to know this commonly followed path in any case, because occasionally, treading this path may be more comfortable to you.
Let us go through this deductive solution,
$\displaystyle\frac{\sqrt{3+x} + \sqrt{3-x}}{\sqrt{3+x} - \sqrt{3-x}}=2$,
Or, $\sqrt{3+x} + \sqrt{3-x} = 2(\sqrt{3+x}- \sqrt{3-x})$,
Or, $\sqrt{3+x} = 3(\sqrt{3-x})$,
Squaring both sides,
$3 + x = 9(3-x) = 27 - 9x$,
Or, $10x = 24$,
Or, $x = \displaystyle\frac{12}{5}$.
Summary
The first solution uses rich algebraic technique of componendo dividendo twice and accurately hands you over the solution in a few steps.
In the second solution, though the given expression seems to be complex at first, if you can mentally consider $\sqrt{3+x}$ and $\sqrt{3-x}$ as single variables, you should also be able to deduce mentally the simple relation between these two so that by squaring both sides you get the solution in just two steps more.
Though this is a deductive approach which generally is to be avoided in such front ranking competitive exams, in this special case, you may adopt this approach also to reach the solution quickly depending on your skill-set.
Guided help on Algebra in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Algebra in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Algebra in Suresolv and is up-to-date.