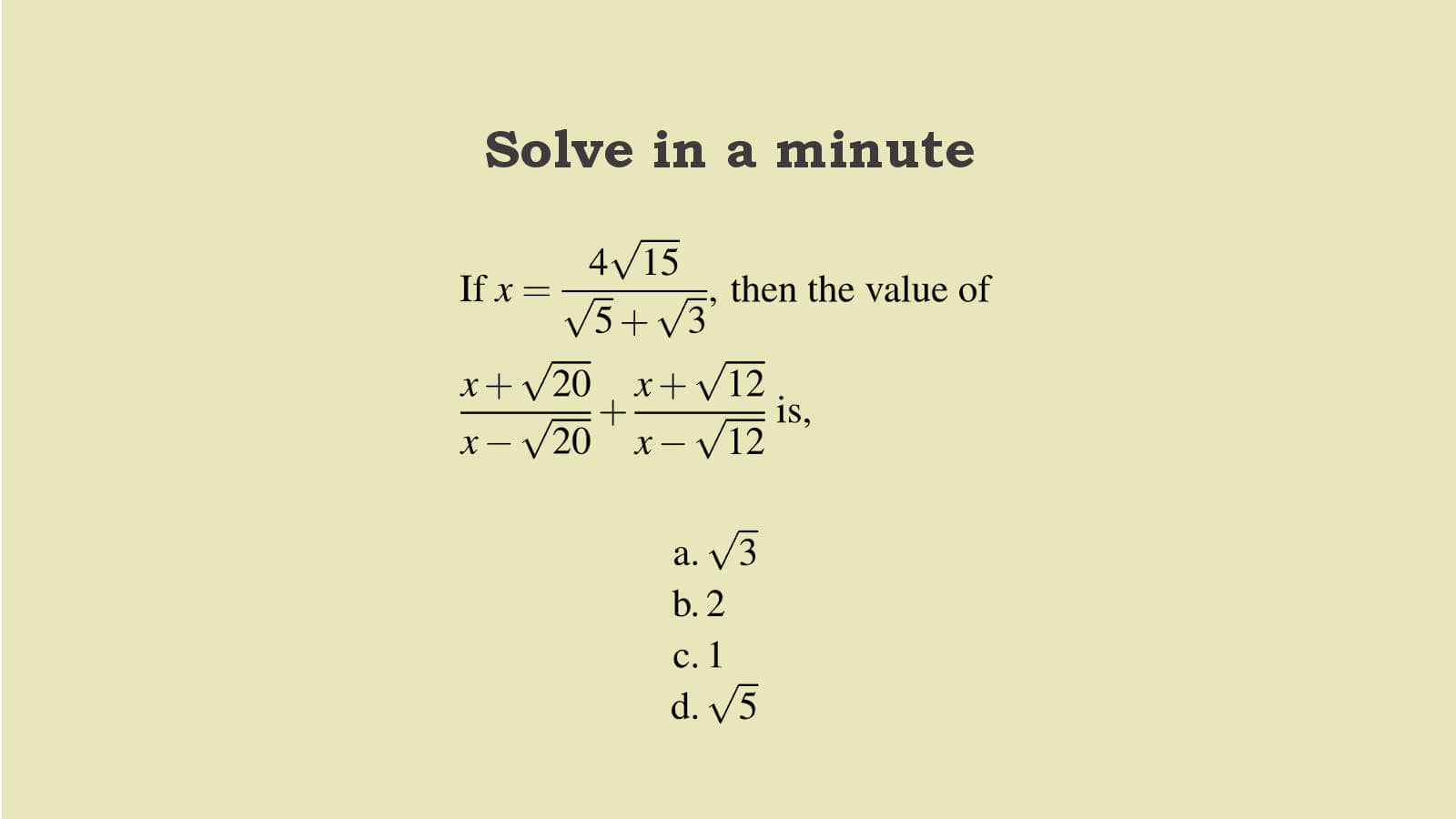
How to solve difficult surds problems in a few simple steps using algebra and surds techniques
Difficult surds problems invariably involve algebra.
How to solve the complex surds problems easily using surds and algebra techniques is shown by solving hand selected surds problems.
Sections are,
- Carefully selected solved problems to highlight how to solve difficult surds problems step by step quickly. Why and how to use the techniques are explained.
- Surds Guide list of all links on Surds: Concept articles, Question and Solution sets on surds show how to solve many types of difficult surds problems quickly.
Recommended reading before you go ahead
How to solve surds part 1, Rationalization of surds
How to solve surds part 2, Double square root surd and surd term factoring
How to solve surds part 3, Surd expression comparison and ranking.
Techniques explained in these tutorials should be enough to solve quickly most of the difficult surds problems that you will face in competitive exams.
Solved Difficult Surds problems
Difficult Surds Problem 1. Double square root surds and Surd term factoring
If $x = \displaystyle\frac{\sqrt{3}}{2}$, then the value of $\displaystyle\frac{\sqrt{1 + x}}{1 + \sqrt{1 + x}} + \displaystyle\frac{\sqrt{1 - x}}{1 - \sqrt{1 - x}}$ is,
- $2$
- $2 - \sqrt{3}$
- $\displaystyle\frac{2}{\sqrt{3}}$
- $1$
Solution: First stage Problem analysis: Simplifying Double square root of surds
First realization:
You must express $(1 + x)$ and $(1 - x)$ as square of sums to solve the problem.
These are double square root surds expressions and you have to simplify these.
Substitute given value of $x$,
$\sqrt{1 + x} = \sqrt{1 + \displaystyle\frac{\sqrt{3}}{2}}$
$=\sqrt{\displaystyle\frac{2 + \sqrt{3}}{2}}$.
First stage transformation of given relation:
The target is more defined now,
Numerator of the surd sum under the root to be expressed as a square that at first glance seems to be not possible.
Recall the general three-term expression of a square of sum,
$(a+b)^2=a^2+2ab+b^2$.
The surd term will be the middle term $2ab$ and the numeric term will be equivalent to sum of first and third terms, $a^2+b^2$.
So your job is to express the surd term $\sqrt{3}$ in $\sqrt{\displaystyle\frac{2 + \sqrt{3}}{2}}$ with a factor of 2.
In this case the middle term factor of 2 is not there. So introduce it by force.
Multiply and divide the term by 2,
$\sqrt{1 + x} =\sqrt{\displaystyle\frac{4 + 2\sqrt{3}}{4}}$
$=\sqrt{\displaystyle\frac{(\sqrt{3} + 1)^2}{4}}$
$=\displaystyle\frac{\sqrt{3} + 1}{2}$.
This is the main breakthrough by simplifying double square root of surds.
The same way,
$\sqrt{1 - x} =\displaystyle\frac{\sqrt{3} - 1}{2}$.
Solution: Second stage simplification of surds problem: Strategy of target simplification first
In any algebraic evaluation of this type, follow the strategy of simplifying target expression first.
Here, the target expression becomes,
$E=\displaystyle\frac{\sqrt{1 + x}}{1 + \sqrt{1+ x}} + \displaystyle\frac{\sqrt{1 - x}}{1 - \sqrt{1 - x}}$
$=\displaystyle\frac{\sqrt{1+x}+\sqrt{1-x}}{[\sqrt{1+x}-\sqrt{1-x}]+[1-\sqrt{1-x^2}]}$.
Evaluate mentally,
$\sqrt{1+x}+\sqrt{1-x}=\displaystyle\frac{\sqrt{3} + 1}{2}+\displaystyle\frac{\sqrt{3} - 1}{2}=\sqrt{3}$,
$\sqrt{1+x}-\sqrt{1-x}=\displaystyle\frac{\sqrt{3} + 1}{2}-\displaystyle\frac{\sqrt{3} - 1}{2}=1$, and,
$1-\sqrt{1-x^2}=1-\sqrt{1-\displaystyle\frac{3}{4}}=1-\displaystyle\frac{1}{2}=\displaystyle\frac{1}{2}$.
Substitute in the intermediate result of target expression,
$E=\displaystyle\frac{\sqrt{3}}{1+\displaystyle\frac{1}{2}}$
$=\displaystyle\frac{\sqrt{3}}{\displaystyle\frac{3}{2}}$
$=\displaystyle\frac{2\sqrt{3}}{3}$.
Take out factor $\sqrt{3}$ from denominator, $3=(\sqrt{3})^2$ by surd term factoring.
Result is,
$E=\displaystyle\frac{2}{\sqrt{3}}$.
Answer: Option c: $\displaystyle\frac{2}{\sqrt{3}}$.
Elegant quick solution without simplifying target expression first
In the second stage directly substitute the values of $\sqrt{1+x}$ and $\sqrt{1-x}$,
$E=\displaystyle\frac{\displaystyle\frac{\sqrt{3} + 1}{2}}{1 + \displaystyle\frac{\sqrt{3} + 1}{2}} + \displaystyle\frac{\displaystyle\frac{\sqrt{3} - 1}{2}}{1 - \displaystyle\frac{\sqrt{3} - 1}{2}}$.
Simplifying,
$E =\displaystyle\frac{\sqrt{3} + 1}{3 + \sqrt{3}} + \displaystyle\frac{\sqrt{3} - 1}{3 - \sqrt{3}}$
Now identify the key pattern that $\sqrt{3}$ can be factored out of both the terms of each denominator.
This results in each denominator factor equal to the numerator canceling each other out,
$E=\displaystyle\frac{\sqrt{3} + 1}{\sqrt{3}(\sqrt{3} + 1)} + \displaystyle\frac{\sqrt{3} - 1}{\sqrt{3}(\sqrt{3} - 1)}= \frac{2}{\sqrt{3}} $.
This is application of the simple but very useful Surd term factoring technique that helps to simplify surds expressions so many times.
Answer: Option c: $\displaystyle\frac{2}{\sqrt{3}}$.
Key concepts used:
- Identifying that double square root simplification must be done first. This must be the first key action.
- Creating forcibly a coefficient of 2 in the surd term, which is the middle term of the three term expansion of square of sum of two terms—$2ab$ in $(a + b)^2$. The basic concept used is—the surd term must be the middle term of the three term expansion of square of sum and it must have coefficient 2.
- In the last stage, apply Strategy of target expression simplification first. And substitute value of $\sqrt{1+x}$ and $\sqrt{1-x}$ in the simplified target.
- Or, without simplifying the target first directly substitute the values in target expression. Simplify by deep application of the unassuming but powerful Surd term factoring technique.
Which solution do you like?
Our choice is the second one in which key pattern identification and surd term factoring together cut-short the calculations.
The first solution is shown,
- To demonstrate that a complex problem can be solved in more than one way. Solving the problem is not the main objective. Goal is to solve it in as few steps as possible.
- For your awareness that it is important to know which path is the easier. And to know that you have to be able to discover more than one path.
To have comprehensive knowledge on simplifying double square root surds and surd term factoring read the tutorial,
Difficult Surds Problem 2. Surd expression comparison and Inequality concepts
If $a = \sqrt{6} - \sqrt{5}$, $b = \sqrt{5} - 2$ and $c = 2 - \sqrt{3}$ then the correct comparative relationship between $a$, $b$ and $c$ is,
- $b \lt a \lt c$
- $a \lt b \lt c$
- $b \lt c \lt a$
- $a \lt c \lt b$
Solution: First stage: Problem analysis to Identify key patterns and Primary action
This is a problem of surd expression comparison, where the two term surd expressions being compared are in the form of subtractions $\sqrt{p+1}-\sqrt{p}$.
This makes direct comparison of the irrational expressions not possible.
First express $2$ as $\sqrt{4}$ to make all four terms $\sqrt{6}$, $\sqrt{5}$, $\sqrt{4}$ and $\sqrt{3}$ similar in their surds form.
Three surds expressions,
$a = \sqrt{6} - \sqrt{5}$,
$b = \sqrt{5} - \sqrt{4}$,
$c = \sqrt{4} - \sqrt{3}$.
Identify the first key pattern,
Difference of squares of the terms in each surds expression is 1.
Now identify the second key pattern that it would have been easy to compare the three if these were additions of two surds terms in the form,
$\sqrt{6}+\sqrt{5}$, $\sqrt{5}+\sqrt{4}$, and $\sqrt{4}+\sqrt{3}$.
Why? Because,
In the two surds expressions $(\sqrt{6}+\sqrt{5})$ and $(\sqrt{5}+\sqrt{4})$, one term $\sqrt{5}$ is common and the expressions are additive.
And $\sqrt{6} \gt \sqrt{4}$. So, $(\sqrt{6}+\sqrt{5}) \gt (\sqrt{5}+\sqrt{4})$.
Convert the subtractive surds expressions to additive by rationalization of surds technique,
Multiply and divide each expression by the form of expression $\sqrt{p+1}+\sqrt{p}$ and then invert each.
This is the most important key action that helps to solve the problem quickly.
Solution: Second stage: Surds expression comparison by Rationalization of surds and Inequality concepts
Invert the three expressions and rationalize,
$\displaystyle\frac{1}{a} = \frac{\sqrt{6} + \sqrt{5}}{(\sqrt{6})^2 - (\sqrt{5})^2}=\sqrt{6} + \sqrt{5} $,
$\displaystyle\frac{1}{b} = \frac{\sqrt{5} + \sqrt{4}}{(\sqrt{5})^2 - (\sqrt{4})^2}=\sqrt{5} + \sqrt{4} $, and,
$\displaystyle\frac{1}{c} = \frac{\sqrt{4} + \sqrt{3}}{(\sqrt{4})^2 - (\sqrt{3})^2}=\sqrt{4} + \sqrt{3} $.
As $\sqrt{5} \gt \sqrt{3}$ and $\sqrt{4}$ common between $\sqrt{5} + \sqrt{4}$ and $\sqrt{4} + \sqrt{3}$,
$\sqrt{5} + \sqrt{4} \gt \sqrt{4} + \sqrt{3}$,
Or, $\displaystyle\frac{1}{b} \gt \displaystyle\frac{1}{c}$.
Similarly as, $\sqrt{6} \gt \sqrt{4}$ and $\sqrt{5}$ common between $\sqrt{6} + \sqrt{5}$ and $\sqrt{5} + \sqrt{4}$,
$\sqrt{6} + \sqrt{5} \gt \sqrt{5} + \sqrt{4}$,
Or, $\displaystyle\frac{1}{a} \gt \displaystyle\frac{1}{b}$.
Join the two inequality relations by Inequality concept:
If $x \gt y$ and $y \gt z$, then $x \gt z$, and $x \gt y \gt z$.
Combined result is,
$\displaystyle\frac{1}{a} \gt \displaystyle\frac{1}{b} \gt \displaystyle\frac{1}{c}$.
Apply Inequality inversion concept,
If $x \gt y$, $\displaystyle\frac{1}{x} \lt \displaystyle\frac{1}{y}$, inverting two sides of an inequality reverses inequality.
Comparative relationship between $a$, $b$ and $c$ obtained as,
$a \lt b \lt c$.
Answer: Option b: $a \lt b \lt c$.
Key concepts used:
- Identifying that the difference of squares of each pair of terms is 1, it was decided to apply Rationalization of surds technique, but to do so the variables were first inverted.
- Rationalization of surds applied on each of the three. Comparing two pairs of additive expressions, clear comparative relation of the two values of the inverted variables could easily be formed.
- Inequality joining concept:;If $x \gt y$ and $y \gt z$, $x \gt y \gt z$.
- Inequality inversion concept: If $x \gt y$, $\displaystyle\frac{1}{x} \lt \displaystyle\frac{1}{y}$.
To know more on how to compare surd expressions, read the article,
How to solve surds part 3 - surd expression comparison and ranking.
Difficult Surds Problem 3. Rationalization of surds, Componendo, Strategy of target simplification first and Surd term factoring
If $x=\displaystyle\frac{4\sqrt{15}}{\sqrt{5} + \sqrt{3}}$, then the value of $\displaystyle\frac{x + \sqrt{20}}{x - \sqrt{20}} + \displaystyle\frac{x + \sqrt{12}}{x - \sqrt{12}}$ is,
- $\sqrt{3}$
- 2
- 1
- $\sqrt{5}$
Solution: First stage: input simplification by rationalization of surds
By applying rationalization of surds on given value of $x$,
$x=\displaystyle\frac{4\sqrt{15}}{\sqrt{5} + \sqrt{3}} = 2\sqrt{15}(\sqrt{5} - \sqrt{3})$.
The given value of $x$ not being simple, we'll follow the very important strategy of target expression simplification first before substituting given value of $x$.
Solution: Second stage: Numerator simplification of both terms of the target expression
Both the terms in the target expression are of the componendo dividendo pattern (or signature of componendo dividendo),
In each fraction term, the two terms in numerator and denominator are same with only one pair opposite in sign.
With such a form of an algebraic fraction, it is easily possible to eliminate one of the numerator terms by adding or subtracting 1.
Question is which of the two numerator terms to eliminate?
Again we take a strategic decision to eliminate the more complex value of $x$. This would achieve greatest simplification of the two terms. This will be the dividendo operation of componendo dividendo.
Subtracting 1 from each of the two terms and adding compensating 2,
$E = \displaystyle\frac{x + \sqrt{20}}{x - \sqrt{20}} -1 + \displaystyle\frac{x + \sqrt{12}}{x - \sqrt{12}} -1 +2$
$=\displaystyle\frac{2\sqrt{20}}{x - \sqrt{20}} + \displaystyle\frac{2\sqrt{12}}{x - \sqrt{12}} +2$
$=\displaystyle\frac{4\sqrt{5}}{2\sqrt{15}(\sqrt{5}-\sqrt{3}) - 2\sqrt{5}} + \displaystyle\frac{4\sqrt{3}}{2\sqrt{15}(\sqrt{5}-\sqrt{3}) - 2\sqrt{3}} +2$.
We have now substituted the value of $x$ and simplified $\sqrt{20}$ as $2\sqrt{5}$ and $\sqrt{12}$ as $2\sqrt{3}$.
Further simplifying by cancelling out $2\sqrt{5}$ and $2\sqrt{3}$ between numerator and denominator of the first and the second terms respectively,
$E=\displaystyle\frac{2}{\sqrt{3}(\sqrt{5}-\sqrt{3}) - 1} + \displaystyle\frac{2}{\sqrt{5}(\sqrt{5}-\sqrt{3}) - 1} +2$
$=\displaystyle\frac{2}{\sqrt{15} - 4} + \displaystyle\frac{2}{4-\sqrt{15}} +2$.
How very convenient! The first two terms cancel out leaving just 2 as the final result,
$E=2$.
In fact, by this strategic approach, the complex problem can even be solved in mind.
Answer: Option b: 2.
Key concepts, techniques and steps:
- First step: Transform given equation to eliminate its denominator by rationalization of surds.
- Second step: Strategy of target expression simplification first adopted.
- In this step, key pattern of componendo dividendo signature in both target terms identified. Decided to eliminate the more complex term $x$ from both the numerators by Componendo - subtracting 1 from each fraction term and adding compensating 2. This is also numerator simplification technique.
- Third step: Value of $x$ substituted. Surd term factoring technique applied on numerator and denominator of each fraction term. Numerator and denominator transformed to same factor for both fractions cancelling each other out leaving the 2 as the final result.
Difficult Surds Problem 4. How to solve a surds equation
What are the real roots of the equation, $\sqrt{3x+4} +\sqrt{3x-6}=10$?
- $\displaystyle\frac{15}{4}$
- $\displaystyle\frac{35}{4}$
- $\displaystyle\frac{25}{4}$
- $\displaystyle\frac{5}{4}$
Solution: Problem analysis and strategy decision
To solve such an equation, first thought is raise it to its square.
Mentally exploring idea a bit, you find that raising the equation to its square would create complexity.
We always seek simplicity. Isn't it?
This is where the key idea of using the result of $(a+b)(a-b)=a^2-b^2$ recalled.
The key pattern that helped is:
The variable term $3x$ is same in both square roots. So if the two are squared and difference taken, result will be simple numeric. That has been the trigger.
Multiply both sides of the equation by $(\sqrt{3x+4} -\sqrt{3x-6})$,
$3x+4 -(3x-6)=10=10(\sqrt{3x+4} -\sqrt{3x-6})$,
Or, $\sqrt{3x+4} -\sqrt{3x-6}=1$.
Add it up with the given equation to eliminate the second term,
$2\sqrt{3x+4} =11$
Square both sides of the equation,
$4(3x+4)=121$,
Or, $12x=105$,
Or, $x=\displaystyle\frac{35}{4}$.
Answer: Option b: $\displaystyle\frac{35}{4}$.
We will solve at the end a completely different type of surds problem.
Difficult Surds Problem 5. Surds problem with surds equation: Comparison of coefficients of similar variables
If $\displaystyle\frac{4+3\sqrt{3}}{\sqrt{7+4\sqrt{3}}}=A + \sqrt{B}$ then $B-A$ is,
- $-13$
- $3\sqrt{3}-7$
- $13$
- $\sqrt{13}$
Solution 5: Problem analysis and solving execution
First convert the denominator surds expression under square root to a square of sum to simplify the double square root of surds,
$7 + 4\sqrt{3}=(2+\sqrt{3})^2$.
Rationalizing the transformed denominator $2+\sqrt{3}$, you get the given expession as,
$(4+3\sqrt{3})(2-\sqrt{3})=A + \sqrt{B}$,
Or, $-1+2\sqrt{3}=A+\sqrt{B}$.
As $\sqrt{B}$ is the surd term it must be equal to the SIMILAR irrational surd term on the LHS. Similarly rational term $A$ must also be equal to $-1$.
This is because,
A surd term being an irrational number with a non-terminating non-repeating decimal component, it cannot be added numerically to a rational number giving a result that you can express with certainty.
Note: Surd form is $\sqrt{n}$ where $n$ has at least one factor as a prime number. Numerically it always has component of a non-terminating non-repeating decimal component and cannot be expressed as a fraction of the rational number form, $\displaystyle\frac{p}{q}$, where both $p$ and $q$ are integers..
This is what we call Coefficient comparison and equalization for similar variables that don't mix together. It follows a fundamental algebraic principle,
In an equation, coefficients of similar type of variables on both sides of the equation must be equal.
Thus,
$A=-1$, and
$2\sqrt{3}=\sqrt{B}$,
Or, $B=12$, and
$B-A=13$.
Answer: Option c: $13$.
To solve this last problem also you needed three methods,
- First, conversion to square of sum surd expression for simplifying the double square root surds,
- Second, rationalization of surds, and
- Third, Coefficient comparison and equalization for similar variables.
By applying these three methods along with Surd term factoring and Surds expression comparison technique, most of the difficult surds problems can be solved.
Key pattern identification and proficiency in algebraic problem solving techniques also are essential for quick solution. After all, these are algebraic problems only. Surds is an additional characteristic.
You will find the many different types of surds algebra problems solved in the solution sets in the link below.
End note
Strategic analytical approach generally results in much faster solution than any other approach.
Overall, the solution of these example problems are rich in learning potential and,
The more difficult is the problem you solve the more things you learn.
Guided help on Surds, fractions and indices in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Surds, fractions and indices in Suresolv, follow the guide,
Suresolv Surds, fractions, Indices reading and practice guide for competitive exams.
The guide list of articles include ALL articles on Surds, fractions and indices in Suresolv and is up-to-date.