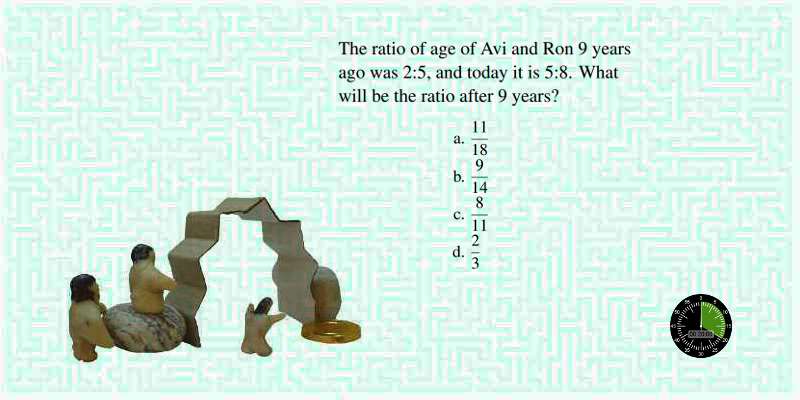
For quick solution of ratio problems use basic concept: Ratio terms are multiples of ratio values
To solve many ratio problems including number system problems quickly, use multiple ratio, componendo dividendo and other quick solution techniques.
The definition of a ratio is,
A ratio expresses how many times one quantity is in comparison to another quantity of same unit.
It is a comparison function. For example, we may express the fact that the age of the son is $\frac{2}{3}$rd of the age of the father as,
$Age_{son} : Age_{father}=2:3$,
where,
$Age_{son}=\text{Age of the son}$, and
$Age_{father}=\text{Age of the father}$.
We call $Age_{son}$ and $Age_{father}$ as the ratio terms or ratio quantities, and the corresponding values of the ratio, 2 and 3 as ratio values.
The ratio terms represent the quantities being compared in the ratio and the ratio values represent how many times one ratio quantity is with respect to the other. The ratio terms must be of same unit.
For mathematical manipulation, such a ratio is needed to be expressed as fractions. In our example then the ratio is expressed in an acceptable form as,
$\displaystyle\frac{Age_{son}}{Age_{father}}=\frac{2}{3}$.
Convention is,
In a proper ratio, the ratio values are always expressed as integers, and as a proper minimized fraction with no common factor between them. This convention ensures uniqueness and clarity of understanding.
In a problem, even if the ratio values are not integers, they need to be converted to integers by multiplying the two values with suitable factors. This is needed to aid manipulation of the ratio values as numerator and denominator of a fraction.
For example, in our problem, the ratio could have been given as,
$Age_{son} : Age_{father}=0.4:0.6$.
To transform this ratio form we will multiply both the numerator and the denominator by the same factor 5 transforming the ratio to,
$Age_{son} : Age_{father}=2:3$.
Ratio quantities are multiples of corresponding ratio values
This is the first most basic concept in the topic of ratio and proportion. It means, in a given ratio,
Actual values of the ratio quantities are not given. The ratio values do not represent the actual values of the ratio quantities, but each of the ratio quantity must be a multiple of its corresponding ratio value.
For example in our problem, the ages of the son and the father could have been 36 years and 54 years or for that matter 50 years and 75 years. For both set of actual values the ratio expression given would have been valid and $2:3$.
In each case though the age of the son would certainly be a multiple of the ratio value of 2 and that of the father a multiple of 3.
Ratio quantities are multiples of corresponding ratio values with a common factor
The second most basic concept is,
The two ratio quantities will always have a common factor 1 or more than 1 which when canceled out, the ratio values are expressed as a minimized proper fraction with no common factor between them. This canceled out common factor will be the HCF between the two quantities being compared so that after canceling out the HCF, the ratio values won't have any common factor left between them.
Alternatively we can state,
Each of the two ratio quantities will always be a multiple of corresponding ratio value, the multiplying factor being 1 or more than 1 and equal for both the ratio quantities, being the HCF between them.
For example, if $Age_{son}=50$ and $Age_{facther}=75$, the HCF of the two will be 25 and after canceling out this HCF, the ratio will finally be expressed as,
$Age_{son}:Age_{facther}=50:75=2:3$.
When the ratio values are given as a proper minimized fraction we won't know what the canceled out HCF was, and so from a ratio we won't know the actual values of the quantities being compared.
Based on this concept we use the technique of reintroducing the HCF in solving majority of the ratio problems. After reintroducing the HCF as a factor of both the ratio values, in the conventional method a linear equation is formed from a equation of fractions before solving it. Though generally not complex, this takes a bit of time.
Instead, using the technique of reintroducing the HCF along with the concept that each ratio quantity must be a multiple of the corresponding ratio value, we can avoid the algebraic process of forming and solving an algebraic equation; by applying multiple enumeration to reach the solution much faster.
We will explore conventional procedural method, mental cross-multiplication method, componendo technique use method and the multiple of ratio value technique in solving two chosen problems and analytically evaluate the efficiency of these approaches.
The multiple of ratio value technique is a rich ratio concept and should give you the quickest and the elegant solution for this type of ratio problems on number or ages.
Chosen Problem 1.
If 12 is added to two numbers, their ratio changes from $3:4$ to $13:16$. The larger number is,
- 48
- 144
- 52
- 36
Problem solving by conventional method, writing down the steps as we do in school
The original ratio of the two numbers $A$ and $B$ is, $A:B=3:4$. Applying the HCF reintroduction technique, we get the actual values of $A$ and $B$ as, $A=3x$ and $B=4x$. Here we have assumed canceled out HCF as $x$, the single unknown variable and the numbers as $A$ and $B$.
After addition of 12 to $A$ and $B$ then the problem status is,
$\displaystyle\frac{3x+12}{4x+12}=\frac{13}{16}$,
Or, $16\times{(3x+12)}=13\times{(4x+12)}$,
Or, $48x+192=52x+156$,
Or, $4x=36$,
Or, $x=9$.
So the larger number $B=4x=36$.
Answer: Option d: 36.
Quick solution of ratio problems: Improvement by delayed evaluation technique
In any case, we need to form the changed status equation of two fractions after addition of 12 to both the numbers. Just like above if you follow the exact steps, it will take you the longest time. This is a fully procedural method that in most cases is the slowest and most inefficient.
We can improve the method by applying delayed evaluation technique which forms a part of broader efficient simplification concepts by avoiding the multiplication,
$\displaystyle\frac{3x+12}{4x+12}=\frac{13}{16}$,
Or, $16\times{(3x+12)}=13\times{(4x+12)}$,
Or, $16\times(3x) +16\times(12)=13\times(4x)+13\times{12}$,
Or, $13\times{4x}-16\times{3x}=12\times{(16-13)}$,
Or, $4x=12\times{3}$,
Or, $x=9$.
So,
$B=4x=36$.
Here we have avoided the multiplication of 12 by 16 and 13, saving valuable seconds.
Note: If you write the steps it will always waste valuable time. That's why we always recommend,
Solve the problem in mind as far as possible.
If you have visualization problem, just write down the changed situation status equation of fractions after addition of 12 to the two numbers and do the rest in your mind.
Further speed up by cross-multiplication and simplification (in mind)
In this method if you are comfortable with mental manipulation of simple expressions and also mental math at simple level, just write down the changed status equation first as,
$\displaystyle\frac{3x+12}{4x+12}=\frac{13}{16}$.
Without forming the equation,
$16\times{(3x+12)}=13\times{(4x+12)}$,
form each term in your mind by cross-multiplication from the fraction, collection of similar terms (in this case subtraction) and then form the simple equation in your mind at the last step.
An effective tactic in this process is to form each term separately.
One can easily arrive at the $x$ term as $52x-48x=4x$, the LHS,
And then $3\times{12}=36$ as RHS.
This will give you the solution much quicker if you are adept in this process.
More improvement of cross-multiplication method
If you avoid writing down even the changed status information forming it in your mind and carry out the rest of the steps, the solution will come still faster. But be aware, unless you are quite skillful in visualization, mental manipulation of expressions, and mental math, you may make mistakes. Our recommendation,
Write down the changed status equation and do the rest mentally.
Conceptually though we are following the conventional method only.
Quick solution of ratio problems by componendo technique
Componendo dividendo is a powerful algebraic technique that frequently can be applied to simplify a particular form of expression in a few seconds. The form of expression it is applied to is,
$\displaystyle\frac{a+b}{a-b}=\frac{5}{2}$, say.
By adding 1 to both sides, then subtracting 1 from both sides, and finally taking the ratio of the two, we get a quick simple result of,
$\displaystyle\frac{a}{b}=\frac{5+2}{5-2}=\frac{7}{3}$.
Many times we apply the first part of the technique, that is componendo technique, to simplify the numerator,
$\displaystyle\frac{a+b}{a-b}+1=\frac{5}{2}+1$,
Or, $\displaystyle\frac{2a}{a-b}=\frac{7}{2}$.
We have simplified the numerator by eliminating $b$.
Using this technique on our problem we get,
$\displaystyle\frac{3x+12}{4x+12}=\frac{13}{16}$,
Or, $\displaystyle\frac{x}{4x+12}=\frac{3}{16}$,
Inverting the LHS and simplifying,
$\displaystyle\frac{4x+12}{x}=\frac{16}{3}$,
Or, $4 + \displaystyle\frac{12}{x}=\frac{16}{3}$,
Or, $\displaystyle\frac{12}{x}=\frac{4}{3}$,
Or $x=9$.
These tasks of adding 1 to fractions, inverting the fraction and so on are simple processes and can be quickly done in mind without using pen and paper. If you are skilled in this type of mental manipulation, this approach should reach you to the solution pretty quick.
Problem solving using Multiple of ratio value technique and multiple enumeration technique, the Elegant Solution
The starting point is nevertheless the equation of fractions representing the status after addition of 12 to both the numbers,
$\displaystyle\frac{3x+12}{4x+12}=\frac{13}{16}$.
In this equation, $3x+12$ must be a multiple of 13 greater than 12. For multiple 26 of 13, we don't get a feasible value of $x$, but for 39, three times 13, we get $x=9$ in a few seconds. Testing it against the denominator takes a few more seconds. With $x=9$, the denominator $4x+12=48$ which is again three times 16 thus satisfying the ratio term relation of $\displaystyle\frac{13}{16}$.
In the first step we have found out a feasible value of $x=9$ that results in a multiple of 13, specifically with factor 3. At the second step, it is checked whether this value of $x$ results in a multiple of 16 that has the same factor of 3. This requirement is a stringent condition for keeping the ratio $\displaystyle\frac{13}{16}$ unchanged.
This should be the fastest and the elegant method if you are skilled in number manipulation and factor multiple concept.
The important point to remember is,
It is up to you to choose the method that suits you, but remember saving seconds counts towards your overall success, and to save seconds and achieve lightning speed, not only would you need to adopt the right method but also you must be highly skilled in applying it.
The many approaches to solve a problem as shown above encourage you to search for alternatives and evaluate them. It is a direct application of the powerful problem solving skill improving Many ways technique.
Let us highlight the power of the Multiple of ratio value technique by solving the second chosen problem.
Chosen Problem 2.
The ratio of age of Avi and Ron 9 years ago was 2:5, and today it is 5:8. What will be the ratio after 9 years?
- $\displaystyle\frac{11}{18}$
- $\displaystyle\frac{9}{14}$
- $\displaystyle\frac{8}{11}$
- $\displaystyle\frac{2}{3}$
Elegant Problem solving by Multiple of ratio value technique
The present age ratio is,
$\displaystyle\frac{Age_{Avi}}{Age_{Ron}}=\frac{5}{8}=\frac{5x}{8x}$, where, $x$ is the HCF of the two ages.
Nine years ago then the age relation was,
$\displaystyle\frac{5x-9}{8x-9}=\frac{2}{5}$.
So $5x-9$ must be a multiple of 2 so that $5x \gt 9$. The first such multiple of 2 in the RHS numerator is 6 with factor of 3 that results in a feasible value of $x$.
For this multiple value 6 in the RHS numerator, $5x-9=6$ and $x=3$.
With $x=3$, denominator $8x-9=15$. As this value of 15 also has the factor 3 with 5, the ratio relation $\displaystyle\frac{2}{5}$ remains unchanged. So $x=3$ satisfies all conditions of the ratio relation of both sides of the equation.
With $x=3$, age ratio after nine years will then be,
$\displaystyle\frac{15+9}{24+9}=\frac{8}{11}$.
Answer: Option C: $\displaystyle\frac{8}{11}$.
Basic concepts application approach
Multiple of ratio value technique uses one of the two basic concepts inherent in a ratio and that's why it usually works faster than other methods for a specific type of number or age problems if properly applied. It works on the most basic conceptual level and is a part of the broader and more powerful Basic concepts application approach which says,
The more basic a concept you use for solving a problem satisfactorily, the more efficient your solution will be.
The method uses mathematical reasoning and is not conventional procedure based.
Resources that should be useful for you
7 steps for sure success in SSC CGL tier 1 and tier 2 competitive tests or section on SSC CGL to access all the valuable student resources that we have created specifically for SSC CGL, but generally for any hard MCQ test.
Concept Tutorials on related topics
Basic concepts on fractions and decimals part 1
Basic concepts on Ratio and Proportion
Componendo dividendo applied on number system and ratio proportion problems
How to solve problems on mixing liquids and based on ages
Basic and Rich Percentage Concepts for solving difficult SSC CGL problems
Efficient solution techniques on related topics
How to solve SSC CGL level arithmetic mixture problems in a few simple steps 1
How to solve SSC CGL level arithmetic mixture problems in a few simple steps 2
How to solve SSC CGL level number and age ratio problems lightning fast
How to solve a tricky SSC CGL level age ratio problem lightning fast
SSC CGL level solved question sets on mixture or alligation
SSC CGL level solved questions sets 78 on mixture or alligation 1
SSC CGL level solved question set 85 on mixture or alligation 2
SSC CHSL level solved question sets on Mixture or Alligation
SSC CHSL level Solved Question set 9 on Mixture or Alligation 1
SSC CHSL level Solved Question set 10 on Mixture or Alligation 2
SSC CGL Tier II level solved question sets on mixture or alligation
SSC CGL Tier II level solved question set 24 on mixture or alligation 1
SSC CGL Tier II level solved question set 25 on mixture or alligation 2
SSC CGL Tier II level question and solution sets on Ratio and Proportion
SSC CGL Tier II level Solution Set 23 Ratio proportion 2
SSC CGL Tier II level Question Set 23 Ratio proportion 2
SSC CGL Tier II level Solution Set 22 Ratio proportion 1
SSC CGL Tier II level Question Set 22 Ratio proportion 1
Other SSC CGL question and solution sets on Ratio and Proportion and Percentage
SSC CGL level Solution Set 84, Ratio proportion 8
SSC CGL level Question Set 84, Ratio proportion 8
SSC CGL level Solution Set 83, Ratio Proportion 7
SSC CGL level Question Set 83, Ratio Proportion 7
SSC CGL level Solution Set 76, Percentage 4
SSC CGL level Question Set 76, Percentage 4
SSC CGL level Solution Set 69, Percentage 3
SSC CGL level Question Set 69, Percentage 3
SSC CGL level Solution Set 68, Ratio Proportion 6
SSC CGL level Question Set 68, Ratio Proportion 6
SSC CGL level Solution Set 31, Ratio and Proportion 5
SSC CGL level Question Set 31, Ratio and Proportion 5
SSC CGL Level Solution Set 25, Percentage, Ratio Proportion 4
SSC CGL level Question Set 25, Percentage, Ratio Proportion 4
SSC CGL level Solution Set 24 Arithmetic Ratio Proportion 3
SSC CGL level Question Set 24, Arithmetic Ratio Proportion 3
SSC CGL level Solution Set 5 Arithmetic Ratio Proportion 2
SSC CGL level Question Set 5 Arithmetic Ratio Proportion 2
SSC CGL level Solution Set 4 Arithmetic Ratio Proportion 1
SSC CGL level Question Set 4, Arithmetic Ratio Proportion 1.