
Graphical method of solution of a pair of linear equations in two variables
NCERT solutions Class 10 maths Chapter 3 Pt 2 covers class 10 graph questions on graphical method of solution of a pair of linear equations. Ex 3.2 solved.
You'll learn now:
- What are the different types of a pair of linear equations—consistent, inconsistent and dependent—with the help of examples of graph questions,
- How to determine the type of a pair of linear equations algebraically—by comparing ratios of parameters of the two equations,
- Graphical method of solution of a pair of linear equations in two variables with examples.
- How to solve Class 10 Graph questions of Exercise 3.2 NCERT.
You may go through the first part of the series before going ahead,
NCERT solutions for class 10 maths Chapter 3 Linear Equations 1 Graphical representation.
What are the three different types of a pair of linear equations—consistent, inconsistent and dependent
We'll start with a problem example.
Example problem 1.
Can you find graphically (or algebraically) the solution to the following problem pairs of linear equations?
- $x-y=8$ and $2x-4y=28$.
- $6x+10y=32$ and $9x+15y=48$, and
- $2x+7y=28$ and $8x+28y=56$.
Solution to example problem 1 (a)—a Consistent pair of linear equations in two variables
To solve the problem graphically, first we'll plot the line for the first equation.
To draw a line for a linear equation you need to find two pairs of (x, y) values for two points that you can accurately mark on the graph.
For the equation $x-y=8$ two such points are, A (8, 0) and B (-2, -10). The first is for $y=0$ and the second is selected by simple trial.
Joining the two and extending in both outward directions you get the straight line.
A few basic concepts on a straight line that includes the concept of slope are explained in the following section.
Slope of a line and a few basic concepts on straight lines
If you plot values of $y$ for different values of $x$ for the linear equation $x-y=8$ on a two axes x-y coordinate system, you will get a straight line.
Every (x, y) value pair represents a point on the line and is called a solution to the equation.
As a straight line consists of infinite number of points on it, there will be infinite number of (x, y) value pairs each of which satisfies the linear equation.
If you draw a graph on a two axes planar coordinate system, its nature will be determined by a parameter at its different points that is called slope.
If the slope of a continuous plot of graph is same for all points on it, the plot of graph is linear, otherwise, with different slopes at different points, the plot of graph is curved.
Slope is defined for a linear (the line may be a straight line or a curved line) graph as inclination of the tangent at a particular point—it means slope is for a point on a linear graph.
Let us first show you the graph corresponding to the equation $x-y=8$.

By definition, the slope of a straight line at a point is given by the relation,
$y=mx+c$, where $m=\tan \theta$ is the slope.
Actually angle $\theta$ becomes the angle of inclination of the line with x-axis.
For the line $x-y=8$ expressed as,
$y=x-8$,
value of slope $m_1=1=\tan 45^0$.
At all points of the line slope remains constant, and that is why the line corresponding to $x-y=8$ is a straight line.
For the curved line segment "Curve" in the figure, the line $x-y=8$ is tangent at point B. So we say, slope of the curved line is 1 at point B.
But this slope changes from point to point on the curve. Again at point C the line $y=-p$ (p is a constant), is tangent to the curve. As this line is parallel to x-axis, it has zero inclination. Slope of this tangent line and the curve at point C is 0.
Let us consider the slope of a line in general form of,
$ax+by+c=0$,
Or, $y=-\displaystyle\frac{a}{b}x-\displaystyle\frac{c}{b}=mx+d$, where $d=-\displaystyle\frac{c}{b}$ is the constant in this form.
Here slope $m$ is,
$m=-\displaystyle\frac{a}{b}$.
We'll see shortly equal slopes of two lines means equal ratios of coefficients of the variables $x$ and $y$.
To draw the second line for the equation $2x-4y=28$, first find a convenient point C (14, 0) by substituting $y=0$ in the equation.
Then select the second convenient point as D (-2, -8) by simple trial. The second point could also have been (0, -7) for $x=0$. Instead, D (-2, -8) is selected because both values of $x$ and $y$ are even and are most convenient to plot accurately on our graph.
Joining the two and extending in both outward directions you would get the second line for equation $2x-4y=28$.
The slope of this line is given by,
$y=\frac{1}{2}x-7$.
So slope for the line is,
$m_2=\frac{1}{2}$.
The two lines intersect at point P with coordinates $\text{(x=2, y=-6)}$. These are the solution values of two variables for the pair of equations.

We say—this pair of linear equations are consistent.
To sum up,
The necessary condition for a pair of linear equations to be consistent is—the two equations must have at least one solution.
When the two corresponding lines intersect at a point, we'll have a unique solution for the pair of consistent linear equations.
But even when the equations are equivalent and the lines coincident these will be termed consistent because of infinitely many solutions. We'll see an example shortly.
So, for a unique solution,
The slopes of the two corresponding lines must be unequal.
In this problem, slope of first line $x-y=8$ is, $m_1=1$ and the slope for the second line $2x-4y=28$ is, $m_2=\frac{1}{2}$.
As $m_1 \neq m_2$, the pair of equations are consistent and have a unique solution.
Solution to example problem 1 (b)—a Consistent pair of equivalent and dependent linear equations in two variables
The two equations are,
$6x+10y=32$ and $9x+15y=48$.
In this case we'll compare the ratios of the coefficients of two variables $x$ and $y$ first.
The conceptual basis of finding the type of pair linear equations algebraically is explained in the following section. If you are aware, you may skip it.
How to determine the type of pair of linear equations algebraically by comparing the ratios of coefficients of two variables and pair of constants
We can express a pair of linear equations in a general form as,
$a_1x+b_1y+c_1=0$, and
$a_2x+b_2y+c_2=0$.
The slopes of the two equations are respectively,
$-\displaystyle\frac{a_1}{b_1}$, and
$-\displaystyle\frac{a_2}{b_2}$.
By comparing first these two ratios you can determine whether the pair of equations have a unique solution or not.
If the slopes of two lines are not equal, the lines will intersect and the two corresponding equations will have a unique solution. This is the case of a consistent pair of equations with a unique solution.
If two slopes are equal,
$-\displaystyle\frac{a_1}{b_1}=-\displaystyle\frac{a_2}{b_2}$,
Or, $\displaystyle\frac{a_1}{a_2}=\displaystyle\frac{b_1}{b_2}$.
This is why in practice, the ratios of coefficients of $x$ and $y$ are compared instead of comparing slopes. The two are equivalent.
But when the ratios of coefficients of two variables are equal, you have to further check the equality of the ratio of the constants.
If the ratios of coefficients of two variables are equal to each other as well as equal to the ratio of constants, the lines will be coincident with infinitely many solutions. These form a dependent pair of equivalent and consistent equations.
The third possibility is,
When ratios of coefficients of two variables are equal to each other but not equal to the ratio of the constants, the two lines will be parallel, will never meet and so won't have any solution. These form a pair of inconsistent linear equations.
As you can see, without drawing the graphs you can determine the type of pair of linear equatiions just by comparing the three parameter ratios of the two equations algebraically.
The three ratios of the two equations $6x+10y=32$ and $9x+15y=48$ are,
$\displaystyle\frac{a_1}{a_2}=\frac{6}{9}=\frac{2}{3}$,
$\displaystyle\frac{b_1}{b_2}=\frac{10}{15}=\frac{2}{3}$, and
$\displaystyle\frac{c_1}{c_2}=\frac{32}{48}=\frac{2}{3}$.
Effectively if you multiply the first equation by $\displaystyle\frac{3}{2}$ you will get the second equation.
We say—the two equations are equivalent and dependent.
As a pair of coincident lines would have infinitely many solutions for infinitely many common points, the pair of equations are also consistent.
Solution to example problem 1 (c)—an Inconsistent pair of linear equations in two variables
We'll compare the ratios of the three parameters of the two equations first for the equations,
$2x+7y=28$ and $8x+28y=56$.
The three ratios are,
$\displaystyle\frac{a_1}{a_2}=\frac{2}{8}=\frac{1}{4}$,
$\displaystyle\frac{b_1}{b_2}=\frac{7}{28}=\frac{1}{4}$, and
$\displaystyle\frac{c_1}{c_2}=\frac{28}{56}=\frac{1}{2}$.
The slopes are equal because the ratio of coefficients of the variables are equal, but the lines are not equivalent as the ratio of variable coefficients are not equal to the ratio of constants.
This is an example of a pair of parallel lines that won't ever meet and so won't have a solution.
That's why the pair of linear equations are inconsistent.
The lines are plotted in the following graphic.

Let us solve one more problem graphically before the solutions of the exercise problems.
Graphical method of solution of a pair of linear equations in two variables
Every point on the first line satisfies the first equation and so is a solution of the first equation.
Same way, every point on the second line satisfies the second equation and so is a solution of the second equation.
So it is easy to conclude that the point which lies on both the straight lines will satisfy both the linear equations and so the x, y value pair at the point of intersection of two lines will be your solution you are trying to find.
Example Problem 2.
Champa went to a 'Sale' to purchase some pants and skirts. When her friends asked her how many of each she had bought, she answered, "The number of skirts is two less than twice the number of pants purchased. Also, the number of skirts is four less than four times the number of pants purchased." Help her friends to find how many pants and skirts Champa bought.
Solution Example Problem 2.
In a word problem you have to decide first which quantities are to be the two variables.
As number of pants and skirts you have to find out, without any further hesitation, you assume variables $x$ and $y$ to represent number of pants and number of skirts respectively in the first step.
At the second step now, you would form the two linear equations.
By the first part of the statements form the first equation as,
$2x-2=y$.
Grab the part statement "two less than twice the number of pants purchased" first because it involves variable $x$. Translate the word statement in mathematical form as LHS of the equation,
$2x-2$.
Then look at what it is equal to and put it as the RHS. As a result the first complete equation is formed as,
$2x-2=y$.
Or, $2x-y=2$.
This is transformation of the equation to a standard form of equation convenient for further work and is the third step.
At the fourth step identify two convenient points on the line to be drawn.
At $y=0$, $x=1$ and $x=0$, $y=-2$. The two points are, (1, 0) and (0, -2).
Join the two and extend.
Similarly form the second equation from the word statement as,
$4x-4=y$,
Or, $4x-y=4$.
Two convenient points are, at $y=0$, $x=1$ and at $x=0$, $y=-4$. The two points are (1, 0) and (0, -4).
Join the two points and extend. You'll get the following graphic with two lines plotted on the same x-y coordinate system.

The two lines intersect at point $\text{P (x=1,y=0)}$.
So the answer is—Champa purchased 1 pant and no shirt.
Now to the solutions.
But it will be good for you, if you first try to answer the questions before going through the solutions.
Solutions to Problems in Exercise 3.2 of NCERT Class 10 maths on Graphical method of solution of a pair of linear equations in two variables
Problem 1.
Form the pair of linear equations in the following problems and find their solutions graphically.
- 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
- 5 pencils and 7 pens together cost Rs.50, whereas 7 pencils and 5 pens together cost Rs. 46. Find the cost of one pencil and that of one pen.
Problem 2.
On comparing the ratios $\displaystyle\frac{a_1}{a_2}$, $\displaystyle\frac{b_1}{b_2}$ and $\displaystyle\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident.
- $5x-4y+8=0$ and $7x+6y-9=0$
- $9x+3y+12=0$ and $18x+6y+24=0$
- $6x-3y+10=0$ and $2x-y+9=0$
Problem 3.
On comparing the ratios $\displaystyle\frac{a_1}{a_2}$, $\displaystyle\frac{b_1}{b_2}$ and $\displaystyle\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations are consistent or inconsistent.
- $3x+2y=5$ and $2x-3y=7$
- $2x-3y=8$ and $4x-6y=9$
- $\displaystyle\frac{3}{2}x+\displaystyle\frac{5}{3}y=7$ and $9x-10y=14$
- $5x-3y=11$ and $10x+6y=-22$
- $\displaystyle\frac{4}{3}x+2y=8$ and $2x+3y=12$
Problem 4.
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically.
- $x+y=5$ and $2x+2y=10$
- $x-y=8$ and $3x-3y=16$
- $2x+y-6=0$ and $4x-2y-4=0$
- $2x-2y-2=0$ and $4x-4y-5=0$
Problem 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Problem 6.
Given the linear equation $2x+3y-8=0$, write another linear equation in two variables such that the geometrical representation so formed is:
- intersecting lines
- parallel lines
- coincident lines
Problem 7.
Draw the graphs of the equations $x-y+1=0$ and $3x+2y-12=0$. Determine the coordinates of the vertices of the triangle formed by these lines and x-axis, and shade the triangular region.
Solution to the problems
Problem 1.i
Form the pair of linear equations in the following problem and find the solution graphically.
- 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Solution 1.i
Assume the two variables $x$ and $y$ to be the number of boys and the number of girls in Class X of the school respectively.
By first part of the statement you get the total number of students in the class as,
$x+y=10$.
This is the first linear equation in two variables.
As number of girls is 4 more than number of boys, you get the second linear equation as,
$y=x+4$.
Convert this in the form of the first equation and get,
$-x+y=4$.
You have to plot these two linear equations as two straight lines in x-y coordinate axes with same origin.
If the two lines intersect at a point, the solution will be the coordinates of the intersection point.
To plot a linear equation, you need two points that you can easily pin-point on the graph paper.
Let us take the equation, $x+y=10$ first.
With $y=0$ and $x=0$, you get the convenient pair of points that can easily be marked as (10, 0) and (0, 10). Join the two points and extend in both directions outwards to get the corresponding straight line.
The following figure shows the straight line.

Next take up the second equation $-x+y=4$.
Find the two points needed easily for $y=0$ and $x=0$ as, (-4, 0) and (0, 4). Join the two points and extend in both directions outwards on the same coordinate system.
Following is the resultant plot of two lines.

The two lines intersect at point P and the coordinates of this point can easily be identified visually as, $x=3$ and $y=7$.
Answer is: Number of boys is 3 and number of girls 7.
Problem 1.ii
Form the pair of linear equations in the following problem and find the solution graphically.
- 5 pencils and 7 pens together cost Rs.50, whereas 7 pencils and 5 pens together cost Rs. 46. Find the cost of one pencil and that of one pen.
Solution 1.ii.
Assume $x$ and $y$ to be the price of a pencil and a pen (in Rs.) respectively.
For the first purchase the total cost is given by the first linear equation,
$5x+7y=50$.
Now form the second equation as total cost of second purchase as,
$7x+5y=46$.
Draw these two lines on the same coordinate system and you'll have your solution as the coordinates of the intersection point, if any.
First we'll show you the two lines plotted on the same coordinate system and then will explain how we have plotted. The following is the graph.

Getting the first point for the first line, $5x+7y=50$ has been easy. With $y=0$ you have $x=10$ and the point $A$ on the x-axis (10, 0).
But then you are stopped by the decimal value 7.14286 of $y$ with $x=0$. You cannot place this point of intersection with the line with y-axis accurately. A second point to draw the line is needed that you can accurately pin-point. This is what we call—a feasible convenient point.
The method to get the feasible convenient second point is to try out integer values for $x$ that would result in a convenient value for $y$ that can be accurately placed.
As mentioned earlier, the situation is not as difficult as it may seem.
With $x=3$ value of $y$ becomes $y=5$ and you can now draw the line through the two points (10, 0) and (3, 5).
In the same way, for the second equation, $7x+5y=46$ you get the first point easily at $x=0$ and $y=9.2$. The second point again cannot be accurately placed on the x-axis with $y=0$.
Adopting the same method of trying out integer values of $x$ that will result in a convenient value of $y$, you get again the point (3, 5) satisfying the second equation.
After drawing the second line corresponding to the equation $7x+5y=46$, the point common to both the straight lines $B$ with coordinates $x=3$, $y=5$ becomes the solution of the two equations.
Answer: Price of 1 pencil is Rs.3 and that of 1 pen is Rs.5.
Problem 2.i
On comparing the ratios $\displaystyle\frac{a_1}{a_2}$, $\displaystyle\frac{b_1}{b_2}$ and $\displaystyle\frac{c_1}{c_2}$, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident.
- $5x-4y+8=0$ and $7x+6y-9=0$
Solution 2.i.
The ratios are of the three parameters of a standard form of linear equation in two variables,
$ax+by+c=0$.
$a$ and $b$ are the coefficients of $x$ and $y$ respectively and $c$ is the constant.
For the two given equations you can mentally calculate the ratios of coefficients of the two variables to be unequal. These are,
$\displaystyle\frac{a_1}{a_2}=\frac{5}{7}$,
$\displaystyle\frac{b_1}{b_2}=\frac{-4}{6}=-\frac{2}{3}$, and
$\displaystyle\frac{c_1}{c_2}=\frac{8}{-9}=-\frac{8}{9}$.
All three ratios are unequal and the lines will intersect at one point to give you a unique solution.
The lines are plotted in the figure below.
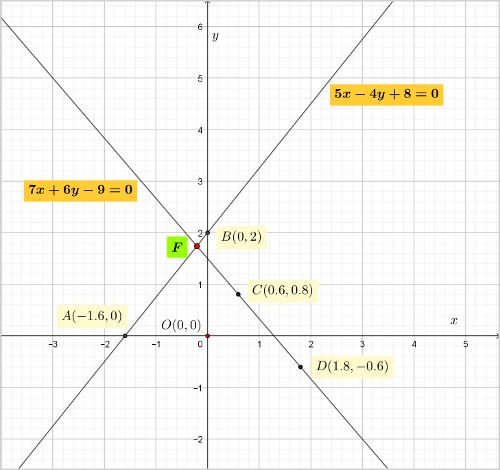
Finding two convenient points for the first equation is easy. The two points are, (-1.6, 0) for $y=0$ and (0, 2) for $x=0$.
But the second line is not so easy to plot. You need to give a little time to find two convenient points by trial, (0.6, 0.8) and (1.8, -0.6).
Once you draw the two lines you will surely get the intersecting point F, but its coordinates are in decimals. Visually you won't know rhe exact values of the coordinates.
This is why Algebraic methods are more suitable to find the solution to this type of pair of equations.
Answer: The lines intersect at a point.
Also the two equations are consistent.
Recommendation: Verify the drawing of these two lines even though you are not asked draw the graphical form. Principle is—take every opportunity to hone your skill.
Problem 2.ii
On comparing the ratios $\displaystyle\frac{a_1}{a_2}$, $\displaystyle\frac{b_1}{b_2}$ and $\displaystyle\frac{c_1}{c_2}$, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident.
- $9x+3y+12=0$ and $18x+6y+24=0$
Solution 2.ii.
The ratios of the two sets of coefficients of $x$ and $y$ and the pair of constants are,
$\displaystyle\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2}$,
$\displaystyle\frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}$, and
$\displaystyle\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}$.
All three ratios being equal, the two lines are coincident and represent a single straight line with infinitely many solutions. By definition, the two equations are consistent.
Answer: The lines are coincident.
Problem 2.iii
On comparing the ratios $\displaystyle\frac{a_1}{a_2}$, $\displaystyle\frac{b_1}{b_2}$, and $\displaystyle\frac{c_1}{c_2}$, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident.
- $6x-3y+10=0$ and $2x-y+9=0$
Solution 2.iii.
$\displaystyle\frac{a_1}{a_2}=\frac{6}{2}=3$,
$\displaystyle\frac{b_1}{b_2}=\frac{-3}{-1}=3$, and
$\displaystyle\frac{c_1}{c_2}=\frac{10}{9}$.
The ratios of coefficients of $x$ and $y$ are equal to each other but not equal to the ratio of constants.
So the slopes of the two lines are equal and the lines are parallel to each other. The pair of equations will have no solution and are inconsistent.
The lines are shown in the graphic below.

Finding the two points for the first line corresponding to $2x-y+9=0$ is easy but it is hard to draw the second line for the equation $6x-3y+10=0$ by hand. Nevertheless, if you manage to draw it, you will find it to be parallel to the first line.
Answer: The lines are parallel to each other.
Problem 3.
On comparing the ratios $\displaystyle\frac{a_1}{a_2}$, $\displaystyle\frac{b_1}{b_2}$, and $\displaystyle\frac{c_1}{c_2}$, find out whether the lines representing the following pairs of linear equations are consistent or inconsistent.
- $3x+2y=5$ and $2x-3y=7$.
- $2x-3y=8$ and $4x-6y=9$.
- $\displaystyle\frac{3}{2}x+\displaystyle\frac{5}{3}y=7$ and $9x-10y=14$.
- $5x-3y=11$ and $10x+6y=-22$.
- $\displaystyle\frac{4}{3}x+2y=8$ and $2x+3y=12$.
Solutions to Problem 3
For Problem 3 i, the two equations are, $3x+2y=5$ and $2x-3y=7$.
We'll compare the ratios of coefficients of $x$ and $y$,
$\displaystyle\frac{a_1}{a_2}=\frac{3}{2}$ and
$\displaystyle\frac{b_1}{b_2}=\frac{2}{-3}=-\frac{2}{3} \neq \displaystyle\frac{a_1}{a_2}$.
So the equations are consistent and the two lines will have a unique intersection solution point. Comparison of the ratio of constants is not required.
Answer: The equations are consistent.
For Problem 3 ii, the two equations are, $2x-3y=8$ and $4x-6y=9$.
We'll compare the ratios of coefficients of $x$ and $y$,
$\displaystyle\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$ and
$\displaystyle\frac{b_1}{b_2}=\frac{-3}{-6}=\frac{1}{2}=\displaystyle\frac{a_1}{a_2}$.
The ratio of the constants being $\displaystyle\frac{c_1}{c_2}=\displaystyle\frac{8}{9} \neq \displaystyle\frac{1}{2}$, the lines are parallel to each other, and will not have any solution. The two equations are then inconsistent.
Answer: The two equations are inconsistent.
For Problem 3 iii, the two equations are, $\displaystyle\frac{3}{2}x+\displaystyle\frac{5}{3}y=7$ and $9x-10y=14$.
We'll compare first the ratios of coefficients of $x$ and $y$,
$\displaystyle\frac{a_1}{a_2}=\displaystyle\frac{\frac{3}{2}}{9}=\frac{1}{6}$ and
$\displaystyle\frac{b_1}{b_2}=\displaystyle\frac{\frac{5}{3}}{-10}=-\frac{1}{6} \neq \displaystyle\frac{a_1}{a_2}$.
So the equations are consistent and the corresponding two straight lines will have a unique intersection solution point.
Answer: The equations are consistent.
For Problem 3 iv, the two equations are, $5x-3y=11$ and $10x+6y=-22$.
We'll first compare the ratios of coefficients of $x$ and $y$,
$\displaystyle\frac{a_1}{a_2}=\frac{5}{10}=\frac{1}{2}$ and
$\displaystyle\frac{b_1}{b_2}=\frac{-3}{6}=-\frac{1}{2} \neq \displaystyle\frac{a_1}{a_2}$.
So the equations are consistent with the two corresponding straight lines having a unique intersection solution point.
Answer: The two equations are consistent.
For Problem 3 v, the two equations are, $\displaystyle\frac{4}{3}x+2y=8$ and $2x+3y=12$.
First compare the ratios of coefficients of $x$ and $y$,
$\displaystyle\frac{a_1}{a_2}=\displaystyle\frac{\frac{4}{3}}{2}=\frac{2}{3}$ and
$\displaystyle\frac{b_1}{b_2}=\frac{2}{3}=\frac{a_1}{a_2}$.
Now compare the ratio of constants,
$\displaystyle\frac{c_1}{c_2}=\frac{8}{12}=\frac{2}{3}$.
Ratios of all three pairs of parameters being equal, the two lines corresponding to the two equations are coincident with infinitely many solutions. So by definition the two equations are consistent.
Answer: The two equations are consistent.
Problem 4.
Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically.
- $x+y=5$ and $2x+2y=10$
- $x-y=8$ and $3x-3y=16$
- $2x+y-6=0$ and $4x-2y-4=0$
- $2x-2y-2=0$ and $4x-4y-5=0$
Solutions to Problem 4.
For problem 4 i, ratio of coefficients of $x$ and $y$ are,
$\displaystyle\frac{a_1}{a_2}=\frac{1}{2}$, and
$\displaystyle\frac{b_1}{b_2}=\frac{1}{2}$.
The ratio of the pair of constants is,
$\displaystyle\frac{c_1}{c_2}=\frac{5}{10}=\frac{1}{2}$.
All three ratios being equal, the two lines corresponding to the two equations are coincident with infinitely many solutions. By definition, the equations are consistent.
Answer: The equations are consistent.
Graphic is shown below.

For problem 4 ii, the equations are, $x-y=8$ and $3x-3y=16$, and ratio of coefficients of $x$ and $y$ are,
$\displaystyle\frac{a_1}{a_2}=\frac{1}{3}$
$\displaystyle\frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3}$.
The ratio of pair of constants is,
$\displaystyle\frac{c_1}{c_2}=\frac{8}{16}=\frac{1}{2}$.
The ratios of coefficients of $x$ and $y$ are equal to each other but not equal to the ratio of constants.
So the slopes of the two lines are equal but the lines are not coincident. The lines are parallel to each other.
The pair of equations will have no solution and are inconsistent.
Answer: The pair of equations are inconsistent.
For problem 4 iii, the equations are, $2x+y-6=0$ and $4x-2y-4=0$ and the ratios of coefficients of $x$ and $y$ are,
$\displaystyle\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$, and
$\displaystyle\frac{b_1}{b_2}=\frac{1}{-2}=-\frac{1}{2}$.
The straight lines corresponding to the two equations will intersect at the solution point P. The equations are consistent. The graphical representation is shown below.

The two equations have a unique solution at the intersection point P with coordinates $x=2$ and $y=2$.
Answer: The equations are consistent.
For problem 4 iv, the equations are, $2x-2y-2=0$ and $4x-4y-5=0$ and the ratios of pairs of coefficients of $x$ and $y$ are,
$\displaystyle\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}$, and
$\displaystyle\frac{b_1}{b_2}=\frac{-2}{-4}=\frac{1}{2}$.
The ratio of the constant terms is,
$\displaystyle\frac{c_1}{c_2}=\frac{-2}{-5} \neq \frac{a_1}{a_2}$.
So the two lines corresponding to the two equations are parallel to each other with no solution and the equations are inconsistent.
Answer: The equations are inconsistent.
Problem 5.
Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution to Problem 5.
Let the length and width of the rectangular garden be $x$ and $y$ in meters respectively.
The perimeter is then,
$2(x+y)$.
By the first statement,
$\displaystyle\frac{1}{2}\times{2(x+y)}=36$,
Or, $x+y=36$.
This is the first equation.
From the second part of the problem description,
$x=y+4$,
Or, $x-y=4$.
Algebraically solution is dead easy. Just add the two equations and you will get,
$2x=36+4=40$,
Or, $x=20$ m, and
$y=20-4=16$ m.
Graphically plotting the two corresponding lines on the same x-y coordinate axes you'll get the following graphic,

The two equations have a unique solution at the intersection point P with coordinates $x=20$ and $y=16$.
Answer: Length of the garden is 20 m and width 16 m.
Problem 6.
Given the linear equation $2x+3y-8=0$, write another linear equation in two variables such that the geometrical representation so formed is:
- intersecting lines
- parallel lines
- coincident lines
Solutions to Problem 6.
For Problem 6 i, to have a second line intersecting with $2x+3y-8=0$, the ratio of the coefficients of variables $x$ and $y$ must be unequal.
For the second line $4x-7y-68=0$, all three parameter ratios (of the coefficients of the two variables and the pair of constants) would be unequal and the two lines would intersect at point P with coordinates (10, -4). The situation is shown below.

Forming such a linear equation is easy. Just arbitrarily change the coefficients and the constant value ensuring that the ratios of the new values to the old values remain unequal.
But you may wonder—how to form such a second equation that is easy to draw on the coordinate system also.
What we did was—
First we have selected an arbitrary point with integer values of coordinates P (10 -4) on the existing first line to be the intersection point of the two lines. We have also decided beforehand that the new line would be formed with opposite signed slope (positive slope in this case, as the given line has negative slope). This would make the new line going down left from upper right direction.
With these two quick decisions, next we selected another convenient point C (17, 0) to be the second point on the new second line. Drawing the line is straightforward now. But still the job of forming the algebraic equation remained unfinished.
How to form a linear algebraic equation from two points in (x, y) coordinate system
Assuming the general form of a line equation, $ax+by+c=0$, and substituting for C (17, 0) we obtained,
$17a=-c$.
Next substituting for P (10, -4), the second relation obtained was,
$10a-4b-17a=0$,
Or, $7a=-4b$.
Now if you fix values $a=4$, and $b=-7$ which are just the opposite valued factors of $a$ and $b$ in the equation $7a=-4b$.
This choice satisfies the relation perfectly and solves the problem. The new equation becomes,
$4x-7y-68=0$.
Answer: The second equation $4x-7y-68=0$ will form the pair of lines intersecting at a unique point.
Solution to Problem 6 ii.
Forming an equation for a line parallel to the line equivalent to $2x+3y-8=0$ is easy.
Keep the coefficients same as 2 and 3 and change the constant to say 12.
Why 12? The reason is—it has both 2 and 3 as factors so that pin-pointing intersecting points with the two axes remains straightforward.
The equation so formed is, $2x+3y-12=0$.
To make the equation look different now multiply all terms with say, 2 and get,
$4x+6y-24=0$.
This is the equation plotted along with the given equation in the following graphic.
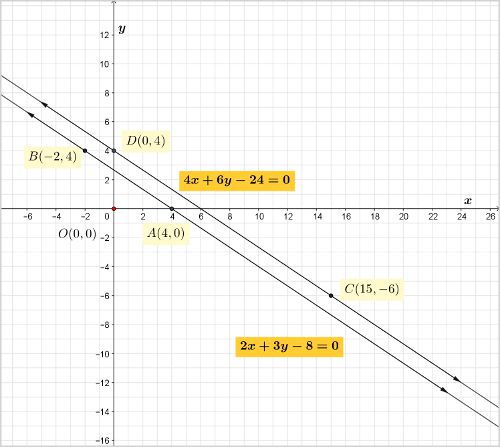
Answer: The second equation $4x+6y-24=0$ will form a pair of lines parallel to each other.
Solution to Problem 6 iii.
This is still easier. Just multiply the whole equation by 2 and get the second line coincident with the given line,
$4x+6y-16=0$.
The graphic is shown below.

Answer: The second equation $4x+6y-16=0$ will form a pair of coincident lins.
Problem 7.
Draw the graphs of the equations $x-y+1=0$ and $3x+2y-12=0$. Determine the coordinates of the vertices of the triangle formed by these lines and x-axis, and shade the triangular region.
Solution to Problem 7.
First the equation $x-y+1=0$ is taken up for plotting. This is a simple equation and the two points on the line needed have been identified as (-1, 0) and (0, 1).
For the second line corresponding to the equation, $3x+2y-12=0$, finding the two points needed has been a simple task—the constant term 12 being multiples of both the coefficients 3 and 2, the x and y axes intersection points identification became straightforward.
With $y=0$, $x=4$ resulted in point (4, 0), and with $x=0$, $y=6$ resulted in point (0, 6).
The two lines intersected at point P (2, 3). The triangle $\triangle PAC$ is formed by the two lines and the x-axis which is shaded blue in the graphic below.
The vertices are, A (-1, 0), P (2, 3) and C (4, 0).
Plotting the two lines has been straightforward. Three of the four points needed for drawing the two lines were taken as intersection points with the two axes,
A (-1, 0), C (4, 0) and D (0, 6).
Instead of the too close y-axis intersection point with line $x-y+1=0$, a second convenient point B (5, 6) has been selected (value of x less than 1 from value of y).
The final graphic is shown below.

Answer: The coordinates of the three vertices are—(2, 3), (-1, 0) and (4, 0).
NCERT Solutions for Class 10 Maths
Chapter 1: Real Numbers
NCERT Solutions for Class 10 Maths on Real numbers part 1, Euclid’s division lemma puzzle solutions
Chapter 2: Polynomials
Chapter 3: Linear Equations
NCERT solutions for class 10 maths Chapter 3 Linear equations 7 Problem Collection
NCERT solutions for class 10 maths Chapter 3 Linear equations 6 Reducing non-linear to linear form
NCERT solutions for class 10 maths Chapter 3 Linear Equations 4 Algebraic solution by Elimination
NCERT solutions for class 10 maths Chapter 3 Linear Equations 3 Algebraic solution by Substitution
NCERT solutions for class 10 maths Chapter 3 Linear Equations 2 Graphical solutions
NCERT solutions for class 10 maths Chapter 3 Linear Equations 1 Graphical representation.
Chapter 4: Quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 1 What are quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 2 Solving by factorization
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 3 Solution by Completing the square
Chapter 6: Triangles
NCERT solutions for class 10 maths chapter 6 Triangles 1 Similarity of Triangles and Polygons
Solutions to Exercise 2 Chapter 6 NCERT X Maths, Characteristics of Similar triangles
Chapter 8: Introduction to Trigonometry, Concepts and solutions to exercise problems
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 1 Trigonometric Ratios
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 4 Trigonometric identities
Chapter 8: Introduction to Trigonometry, only solutions to selected problems
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 6
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 5
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 4
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 3
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 2
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 1