Algebraic method of Substitution for Solving linear equations in two variables
Algebraic Method of Substitution for Solving Linear Equations explained in part 3 of NCERT Solutions Class 10 maths Ch 3. Exercise 3.3 questions solved.
In this third of the seven part series we'll cover,
- Basic concept behind algebraic method of substitution for solving linear equations in two variables (with examples).
- Algebraic method of substitution for solving linear equationsin two variables (with examples).
- Result of applying the algebraic method of substitution on a pair of equivalent linear equations (represented by a pair of parallel lines).
- Solution to Exercise 3.3 of NCERT maths Class 10 on Algebraic Method of Substitution for Solving Linear Equations.
You may directly move on to any of the above sections by clicking on its link and return by clicking browser back arrow.
Basic concept behind algebraic method of substitution for solving linear equations in two variables
We'll start with a problem example.
Example problem 1.
Can you find algebraically the solution to the following problem pairs of linear equations?
- $x-y=8$ and $2x-4y=28$.
- $2x-y=20$ and $3x+5y=43$, and
- $3x+2y=5$ and $2x-3y=7$.
Solution to example problem 1 (a)—algebraic solution of a pair of linear equations in two variables
The two equations are,
$x-y=8$ and,
$2x-4y=28$.
Without knowing any method, the easiest way seems to solve the two equations by multiplying the first equation all through by 2 to get,
$x-y=8$,
Or, $2x-2y=16$.
Then subtracting this equation from the second equation, $2x-4y=28$ to get,
$-2y=12$,
Or, $y=-6$.
Finally, Substituting the value of $y=-6$ in any of the equations, say the first equation, to get,
$x-y=8$,
Or, $x+6=8$,
Or, $x=2$.
Solution is $x=2$, $y=-6$.
Easy and intuitive. Can be done in mind very quickly.
Forget for a moment that you have multiplied the first equation by 2 and then subtracted.
Just consider the result of the subtraction from which you obtained the value of $y$. It has been,
$-2y=12$.
This is a linear equation in one variable. An algebraic truth is,
You can always find the unique value of the variable from a linear equation in one variable.
This is the most basic mechanism which is used invariably by all the algebraic methods that you'll learn for solving two linear equations.
Algebraic method of substitution for solving linear equations
The algebraic truth in solving linear equations is,
In the algebraic methods, effectively one of the two variables is eliminated first, resulting in one linear equation in one variable. Value of the variable obtained from the single linear equation is then substituted in any of the equations in two variables to reduce it to a second equation in only the second variable.
We may generalize this algebraic truth in stating,
For a unique solution, there must be $n$ number of distinct linear equations in $n$ number of variables.
The word 'distinct' signifies,
No two equations in the set to be equivalent (with ratios of all three parameters equal) or ratio of coefficients of two variables equal (corresponding to two lines parallel).
We have already seen examples of these two special cases in our last session, when you couldn't have a unique solution of two linear equations in two variables.
The distinctiveness of the set of equations is important because say, if two equations of the set were equivalent, effectively number of equations reduces by 1 to $(n-1)$. And with $(n-1)$ equations in $n$ variables you can't find a unique solution.
For example, in a two equation set in two variables, if the equations are equivalent, effectively the number of equations reduces to 1 resulting in infinitely many solutions.
Solution to example problem 1 (b)—solution of a pair linear equations algebraically by variable substitution
In this example, we'll solve the two equations by variable substitution.
The two equations are,
$2x-y=20$ and,
$3x+5y=43$.
We'll express one variable, say, $y$ (as it is convenient without creating any fractions), in terms of the second variable $x$ from the first equation. This is the first step. You'll get,
$2x-y=20$,
Or, $y=2x-20$.
In the second step you'll substitute this expression of $y$ in terms of $x$ in place of $y$ in the second equation to get,
$3x+5y=43$,
Or, $3x+5(2x-20)=43$,
Or, $13x-100=43$,
Or, $13x=143$
So, $x=11$.
In the third step now, substitute the value 11 of $x$ thus obtained in any of the two variable equations, say in $2x-y=20$ (because it is simpler), to get,
$2\times{11}-y=20$,
Or, $y=22-20=2$.
Solution is, $x=11$, and $y=2$.
We'll solve now a second example pair of linear equations in two variables by substitution.
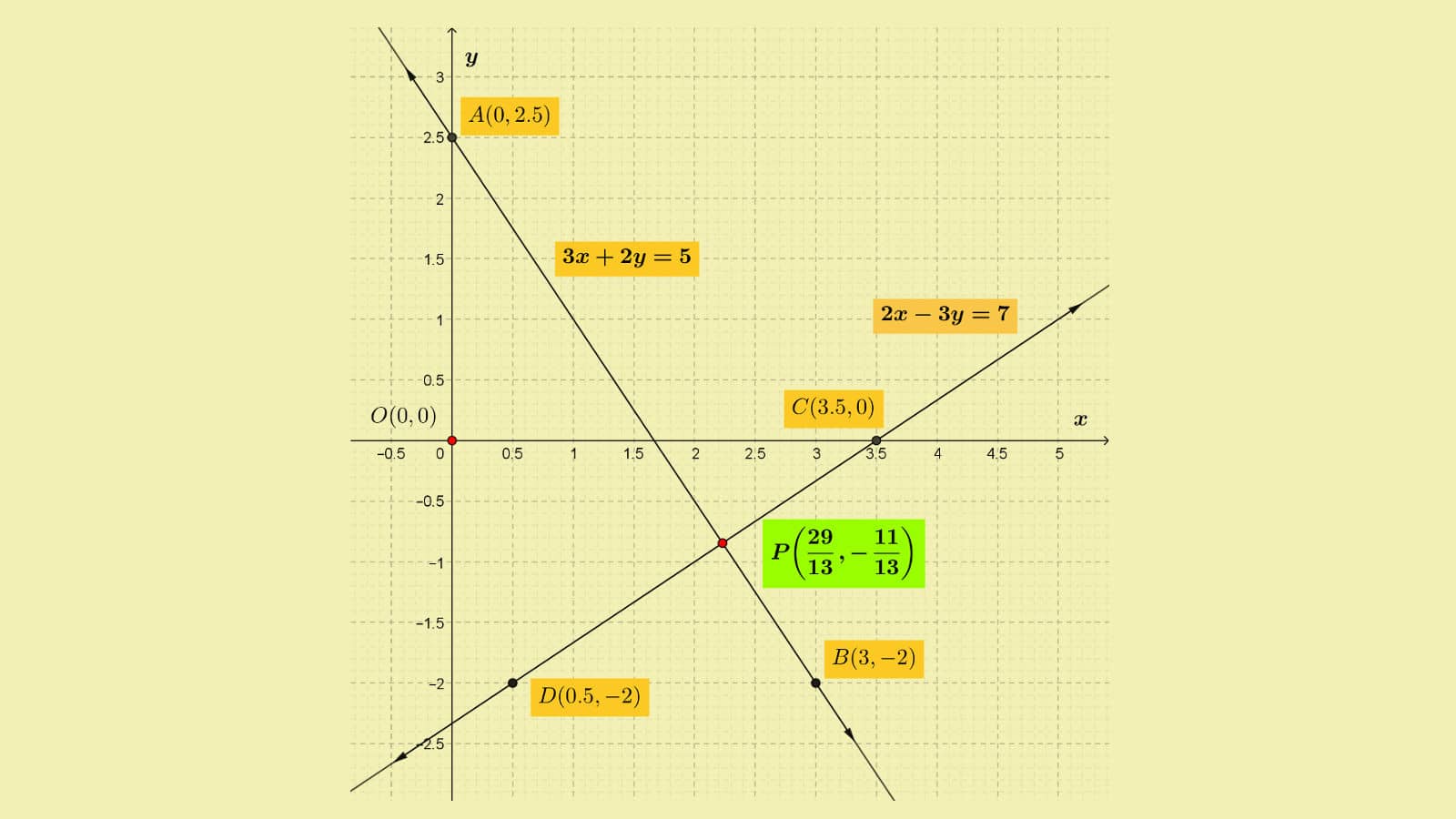
Solution to example problem 1 (c)—a second example of algebraic solution of two linear equations in two variables by substitution
This example has been taken from the earlier session where you could identify the pair of linear equations as consistent having a unique solution, but didn't have to find this solution graphically.
You will understand the difficulty in solving this pair of equations graphically once you solve it algebraically.
The limitation of graphical solution of a pair of linear equations lies in the fact that,
Finding the solution of a pair of linear equations where solution is with decimals or in fractional form is perfectly acceptable in algebraic methods, but may not be possible to place on a graph accurately (when intersection point coordinates involve decimal values).
The two equations we'll solve this time are,
$3x+2y=5$ and,
$2x-3y=7$.
In the first step, Express $y$ in terms of $x$ from the first equation. You'll get,
$3x+2y=5$,
Or, $y=\displaystyle\frac{5-3x}{2}$.
In the second step substitute this expression value of $y$ in the second equation to eliminate $y$ and get,
$2x-3\times{\displaystyle\frac{5-3x}{2}}=7$,
Or, $4x-(15-9x)=14$,
Or, $13x=29$,
Or, $x=\displaystyle\frac{29}{13}$.
In the third step substitute this value of $x=\displaystyle\frac{29}{13}$ in the second equation to get,
$2\times{\displaystyle\frac{29}{13}}-3y=7$,
Or, $58-39y=91$,
Or, $-39y=33$,
Or, $y=-\displaystyle\frac{11}{13}$.
Solution is, $x=\displaystyle\frac{29}{13}$, and $y=-\displaystyle\frac{11}{13}$.
It is easy to find the solution in terms of fraction values algebraically. But as in both values a prime number 13 is the divisor, both values are with infinite sequence of repeating decimals that do not terminate.
Note: Being rational fractions with prime number divisor, both decimal sequences must repeat and be non-terminating. With non-repeating non-terminating digit sequence, the values would have been irrational.
And you can see now that you won't be able to place this solution point accurately on the graph. You may write the fraction coordinate values after finding the values algebraically, but without algebraic method, only graphically you won't be able to find the solution values.
Simply speaking, graphical method of plotting linear equations on a graph and finding solution, visually gives you an idea of the situation, and thereby makes your concept clear.
But in general,
Only Algebraic methods are feasible in practice for solving two linear equations in two variables.
The graphical plot of the situation is shown below.

Result of applying algebraic method of substitution on a pair of equivalent or inconsistent linear equations
Now we'll take up solving two problems to show you what happens if you try to solve a pair of linear equations in two variables that are inconsistent, and that result in a pair of coincident or parallel straight lines.
Example Problem 2.
Find the solution of the following pair of linear equations algebraically.
- $6x-3y+10=0$ and $2x-y+9=0$
- $9x+3y+12=0$ and $18x+6y+24=0$
Solution to Example Problem 2 (a)—No solution as the corresponding two lines are parallel
We'll compare the ratios of coefficients of $x$ and $y$ and the constants of the two equations,
$6x-3y+10=0$ and,
$2x-y+9=0$.
The ratios are,
$\displaystyle\frac{a_1}{a_2}=\frac{6}{2}=3$,
$\displaystyle\frac{b_1}{b_2}=\frac{-3}{-1}=3$, and
$\displaystyle\frac{c_1}{c_2}=\frac{10}{9} \neq \displaystyle\frac{a_1}{a_2}$.
The ratios of coefficients of $x$ and $y$ are equal to each other but not equal to the ratio of constants.
So the slopes of the two lines are equal and the lines are parallel to each other. The pair of equations will have no solution and are inconsistent.
Let's take up solving the problem algebraically.
The second simpler equation is,
$2x-y+9=0$,
Or, $y=2x+9$.
Substitute this expression for $y$ in the first equation $6x-3y+10=0$ to get,
$6x-3(2x+9)+10=0$,
Or, $27=10$, an invalidity.
The two equations cannot have any pair of (x, y) values that would satisfy both the equations.
Solution to Example problem 2 (b)—a pair of coincident lines
The two equations are,
$9x+3y+12=0$ and,
$18x+6y+24=0$.
You can easily see that the ratios of the three parameters of the two equations have the same value $\displaystyle\frac{1}{2}$. The two lines are coincident with infinitely many solutions. The equations are equivalent.
To solve the equations algebraically let's first simplify the first equation by cancelling out the factor of 3 from all three parameter values of 9, 3 and 12. The first equation is thus simplified to,
$3x+y+4=0$,
Or, $y=-(3x+4)$.
Substitute in the second equation and get,
$18x-6\times{(3x+4)}+24=0$,
Or, $18x=18x$, an equation with infinite many values of $x$.
Now we will take up the task of solving the problem in the Exercise 3.3 of Chapter 3.
Solution to Exercise 3.3 of NCERT Class 10 maths Chapter 3 on Algebraic method of substitution for solving linear equations
Problem 1.
Solve the following pair of linear equations by the substitution method.
- $x+y=14$ and $x-y=4$
- $s-t=3$ and $\displaystyle\frac{s}{3}+\displaystyle\frac{t}{2}=6$
- $3x-y=3$ and $9x-3y=9$
- $0.2x+0.3y=1.3$ and $0.4x+0.5y=2.3$
- $\sqrt{2}x+\sqrt{3}y=0$ and $\sqrt{3}x-\sqrt{8}y=0$
- $\displaystyle\frac{3x}{2}-\displaystyle\frac{5y}{3}=-2$ and $\displaystyle\frac{x}{3}+\displaystyle\frac{y}{2}=\displaystyle\frac{13}{6}$
Problem 2.
Solve $2x+3y=11$ and $2x-4y=-24$ and hence find the value of '$m$' for which $y=mx+3$.
Problem 3.
Form the pair of linear equations for the following problems and find their solution by substitution method.
- The difference between two numbers is 26 and one number is three times the other. Find them.
- The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
- The coach of a cricket team buys 7 bats and 6 balls for Rs.3800. Later she buys 3 bats and 5 balls for Rs.1750. Find the cost of each bat and each ball.
- The taxi charges in a city consists of a fixed charge together with the charge for distance covered. For a distance of 10 km the charge paid is Rs.105 and for a journey of 15 km, the charge paid is Rs.155. What are the fixed charges and the charge per km? How much does a person have to pay for a journey of 25 km?
- A fraction becomes $\displaystyle\frac{9}{11}$, if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes $\displaystyle\frac{5}{6}$. Find the fraction.
- Five years hence, the age of Jacob will be three times that of his son. Five years ago Jacob's age was seven times that of his son. What are their present ages?
Solution to the problems in Exercise 3.3 of NCERT Class 10 Chapter 3
Problem 1.i.
Solve the following pair of linear equations by the substitution method.
- $x+y=14$ and $x-y=4$.
Solution to Problem 1.i.
The first equations is,
$x+y=14$,
Or, $y=14-x$.
Substitute expression of $y$ into the second equation $x-y=4$ and you get,
$x-(14-x)=4$,
Or, $2x=18$,
Or, $x=9$.
Substitute value of $x=9$ into the expression for $y$,
$y=14-x=14-9=5$.
Solution is, $x=9$, $y=5$.
Verification: Substitute values of $x$ and $y$ in the LHSs of both the equations to get respectively,
$9+5=14$, and
$9-5=4$.
The values thus satisfy both the equations and indeed is the correct solution to the equations.
Verification takes little time, but makes you confident that your solution is the correct one.
Problem 1.ii.
Solve the following pair of linear equations by the substitution method.
- $s-t=3$ and $\displaystyle\frac{s}{3}+\displaystyle\frac{t}{2}=6$.
Solution to Problem 1.ii.
The two variables are $s$ and $t$.
First equation is,
$s-t=3$,
Or, $t=s-3$
Substitute this into the second equation to get,
$\displaystyle\frac{s}{3}+\displaystyle\frac{t}{2}=6$,
Or, $\displaystyle\frac{s}{3}+\displaystyle\frac{s-3}{2}=6$
Multiply the equation by 6 to get rid of the denominators. 6 because it is the LCM of the two denominator vales 3 and 2.
This is called normalization of linear equations with fraction coefficients.
The changed equation is,
$2s+3(s-3)=36$,
Or, $5s=45$,
Or, $s=9$.
Substitute this value of $s$ into the expression for $t$ to get,
$t=s-3=9-3=6$.
Solution is, $s=9$, and $t=6$.
Verification: Substitute the values of $s$ and $t$ in the LHSs of the two equations to get respectively,
$9-6=3$, and
$3+3=6$.
The values satisfy both the equations and so is the correct solution. Verification increases your confidence on the solution.
Problem 1.iii.
Solve the following pair of linear equations by the substitution method.
- $3x-y=3$ and $9x-3y=9$
Solution to Problem 1.iii.
From the first equation express $y$ in terms of $x$ as,
$y=3x-3$.
Substitute this into second equation to get,
$9x-3(3x-3)=9$,
Or, $9=9$.
The equations are equivalent and the corresponding lines are coincident with infinite many solutions.
Problem 1.iv
Solve the following pair of linear equations by the substitution method.
- $0.2x+0.3y=1.3$ and $0.4x+0.5y=2.3$
Solution to Problem 1.iv.
First multiply both equations by 10 to convert the decimal coefficients to integers getting,
$2x+3y=13$, and
$4x+5y=23$.
From the first equation form,
$y=\displaystyle\frac{13-2x}{3}$.
Substitute this into the expression for $y$ to get,
$y=5\times{\displaystyle\frac{13-2x}{3}}=23$,
Or, $12x+65-10x=69$,
Or, $2x=69-65=4$,
Or, $x=2$.
Substitute this value of $x$ into the expression for $y$ to get,
$y=\displaystyle\frac{13-2x}{3}=\frac{9}{3}=3$.
Solution is, $x=2$, $y=3$.
Verification: Substitute these two values to the LHSs of the first and second equation respectively to get,
$4+9=13$, and
$8+15=23$.
The $x$ and $y$ values of 2 and 3 satisfy both the equations and indeed is the correct solution for the two linear equations.
Problem 1.v.
Solve the following pair of linear equations by the substitution method.
- $\sqrt{2}x+\sqrt{3}y=0$ and $\sqrt{3}x-\sqrt{8}y=0$
Solution to Problem 1.v.
From the first equation get the expression of $y$ in terms of $x$ as,
$y=-\sqrt{\displaystyle\frac{2}{3}}x$.
Substitute this expression into the second equation to get,
$\sqrt{3}x+\displaystyle\frac{4}{\sqrt{3}}x=0$,
Or, $x\left(\sqrt{3}+\displaystyle\frac{4}{\sqrt{3}}\right)=0$.
So $x$ must be equal to 0.
Substitute this value of $x$ in the expression of $y$ to get,
$y=-\sqrt{\displaystyle\frac{2}{3}}x=0$.
Solution is, $x=0$ and $y=0$.
Verification: Substitute the values of $x$ and $y$ into the two equations to easily verify the correctness of the solution.
Problem 1.vi.
Solve the following pair of linear equations by the substitution method.
- $\displaystyle\frac{3x}{2}-\displaystyle\frac{5y}{3}=-2$ and $\displaystyle\frac{x}{3}+\displaystyle\frac{y}{2}=\displaystyle\frac{13}{6}$
Solution to Problem 1.vi.
Multiply both the equations by 6 to get rid of the fraction coefficients and constants. 6 because it is the LCM of the denominator values 3 and 2.
The two changed equatins are then,
$9x-10y=-12$, and
$2x+3y=13$.
From the first equation get,
$y=\displaystyle\frac{9x+12}{10}$.
Substitute this expression into the second equation to get,
$2x+3\times{\displaystyle\frac{9x+12}{10}}=13$,
Or, $20x+27x+36=130$,
Or, $47x=94$,
Or, $x=2$.
Substitute this value into the expression of $y$ in terms of $x$ to get,
$y=\displaystyle\frac{9x+12}{10}=3$.
Solution is, $x=2$ and $y=3$.
Verification: Substitute these values of $x$ and $y$ in LHSs of both the equations to get respectively,
$3-5=-2$, and
$\displaystyle\frac{2}{3}+\displaystyle\frac{3}{2}=\displaystyle\frac{13}{6}$.
The values of $x$ and $y$ satisfy both the equations and so represent the correct solution.
Problem 2.
Solve $2x+3y=11$ and $2x-4y=-24$ and hence find the value of '$m$' for which $y=mx+3$.
Solution to Problem 2.
The two equations are,
$2x+3y=11$ and,
$2x-4y=-24$
From the first equation get $y$ in terms of $x$ as,
$y=\displaystyle\frac{11-2x}{3}$.
Substitute this expression for $y$ into the second equation to get,
$2x-4\times{\displaystyle\frac{11-2x}{3}}=-24$,
Or, $6x-44+8x=-72$,
Or, $14x=-28$,
Or, $x=-2$.
Substitute this value of $x$ in the equation for $y$ to get,
$y=\displaystyle\frac{11-2x}{3}=\frac{15}{3}=5$.
Solution is, $x=-2$, and $y=5$.
Now the second part of the problem.
If these values are to satisfy the equation $y=mx+3$, substitute these values of $x$ and $y$ in the equation and get,
$5=-2m+3$,
Or, $2=-2m$,
Or, $m=-1$.
Answer: $m=-1$.
Meaning of this is—the two lines intersect at (-2, 5) and the third line, $y=-x+3$ with slope as $m=-1$ also passes through this point (-2, 5).
Note: At the start, this second part seemed a bit mysterious. Principle is—Solve a problem part by part. Don't think of the second part while you are solving the first part of a problem.
Problem 3.
Form the pair of linear equations for the following problems and find their solution by substitution method.
- The difference between two numbers is 26 and one number is three times the other. Find them.
- The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
- The coach of a cricket team buys 7 bats and 6 balls for Rs.3800. Later she buys 3 bats and 5 balls for Rs.1750. Find the cost of each bat and each ball.
- The taxi charges in a city consists of a fixed charge together with the charge for distance covered. For a distance of 10 km the charge paid is Rs.105 and for a journey of 15 km, the charge paid is Rs.155. What are the fixed charges and the charge per km? How much does a person have to pay for a journey of 25 km?
- A fraction becomes $\displaystyle\frac{9}{11}$, if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes $\displaystyle\frac{5}{6}$. Find the fraction.
- Five years hence, the age of Jacob will be three times that of his son. Five years ago Jacob's age was seven times that of his son. What are their present ages?
Solution to Problem 3.i.
Form the pair of linear equations for the following problem and find the solution by substitution method.
- The difference between two numbers is 26 and one number is three times the other. Find them.
Let the larger number be $x$ and the smaller $y$.
As their difference is 26 the first linear equation formed is,
$x-y=26$.
Again, the larger number is three times the smaller. So the second equation formed is,
$x=3y$.
Substitute this value of $x$ in the first equation,
$3y-y=26$,
Or, $2y=26$,
Or, $y=13$.
And $x=3y=39$.
Solution is, $x=39$ and $y=13$.
Solution to Problem 3.ii.
Form the pair of linear equations for the following problem and find the solution by substitution method.
- The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
By definition, sum of two angles supplementary to each other is $180^0$.
Let's assume the larger angle as $x$ and the smaller as $y$.
Their difference is 18 degrees. So,
$x-y=18$.
And by the nature of the angles their sum is 180 degrees. So,
$x+y=180$
From the first equation get $y=x-18$ and substitute in the second equation,
$x+(x-18)=180$,
Or, $2x=198$,
Or, $x=99$.
Substitute in $y$ relation in terms of $x$,
$y=x-18=99-18=81$.
Solution is, $x=99$ degrees and $y=81$ degrees.
Solution to Problem 3.iii.
Form the pair of linear equations for the following problem and find the solution by substitution method.
- The coach of a cricket team buys 7 bats and 6 balls for Rs.3800. Later she buys 3 bats and 5 balls for Rs.1750. Find the cost of each bat and each ball.
Let $x$ be the cost of a bat and $y$ be the cost of a ball in rupees.
For the first purchase the linear equation formed for total cost of the purchase is,
$7x+6y=3800$.
And for the second purchase the second equation formed for total cost of purchase is,
$3x+5y=1750$.
Form the expression of $y$ in terms of $x$ from the first equation as,
$y=\displaystyle\frac{3800-7x}{6}$.
Substitute this expression for $y$ in the second equation,
$3x+5\times{\displaystyle\frac{3800-7x}{6}}=1750$,
Or, $18x+19000-35x=10500$,
Or, $17x=8500$,
Or, $x=500$.
Substitute this value of $x$ into the expression for $y$ and get,
$y=\displaystyle\frac{3800-7x}{6}=\displaystyle\frac{3800-3500}{6}=50$.
Solution is, Cost of a bat is $x=500$ rupees, and cost of a ball is $y=50$ rupees.
Solution to Problem 3.iv.
Form the pair of linear equations for the following problem and find the solution by substitution method.
- The taxi charges in a city consists of a fixed charge together with the charge for distance covered. For a distance of 10 km the charge paid is Rs.105 and for a journey of 15 km, the charge paid is Rs.155. What are the fixed charges and the charge per km? How much does a person have to pay for a journey of 25 km?
Let the fixed unknown charge be $x$ and the per km variable charge be $y$ in rupees.
For the first journey the first equation representing the total cost is,
$x+10y=105$.
For the second journey the second equation representing the total cost of journey is,
$x+15y=155$.
From the first equation form $x$ in terms of $y$ as,
$x=105-10y$,
Substitute this expression in the second equation to get,
$(105-10y)+15y=155$,
Or, $5y=50$,
Or, $y=10$.
Substitute this value of $y$ in expression for $x$,
$x=105-10y=105-100=5$.
Solution is, fixed charge is rupees 5 and variable charge is rupees 10 per km.
Now the second part.
For a total journey of 25 km, the equation for total cost will be,
$x+25y=5+250=255$ rupees.
Answer for second part is, cost of 25 km journey will be Rs.255.
Solution to Problem 3.v.
Form the pair of linear equations for the following problem and find the solution by substitution method.
- A fraction becomes $\displaystyle\frac{9}{11}$, if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes $\displaystyle\frac{5}{6}$. Find the fraction.
Let the numerator and denominator of the fraction be $x$ and $y$ respectively.
In the first case then, when both the numerator and denominator was increased by 2, the fraction $\displaystyle\frac{x}{y}$ changes to,
$\displaystyle\frac{x+2}{y+2}=\frac{9}{11}$.
Cross-multiply and get,
$11(x+2)=9(y+2)$,
Or, $11x-9y+4=0$.
This is the first linear equation.
In the second case when both the numerator and denominator have been increased by 3 the fraction changes to,
$\displaystyle\frac{x+3}{y+3}=\frac{5}{6}$,
Or, $6(x+3)=5(y+3)$,
Or, $6x-5y+3=0$.
Form an expression of $y$ in terms of $x$ from the first equation,
$y=\displaystyle\frac{11x+4}{9}$.
Substitute this expression for $y$ in the second equation,
$6x-5\times{\displaystyle\frac{11x+4}{9}}+3=0$
Or, $54x-55x-20+27=0$,
Or, $x=7$.
Substitute this value of $x$ in the expression of $y$,
$y=\displaystyle\frac{11x+4}{9}=\frac{81}{9}=9$.
Solution is: the fraction is, $\displaystyle\frac{7}{9}$.
Solution to Problem 3.vi.
Form the pair of linear equations for the following problem and find the solution by substitution method.
- Five years hence, the age of Jacob will be three times that of his son. Five years ago Jacob's age was seven times that of his son. What are their present ages?
Let present age of Jacob and his son be $x$ years and $y$ years.
For the first condition, after 5 years, the equation representation of the situation is,
$x+5=3(y+5)$,
Or, $x-3y-10=0$.
For the second condition equation representation of the situation of five years back is,
$x-5=7(y-5)$,
Or, $x-7y+30=0$.
Forming value of $x$ from the first equation in terms of $y$ you get,
$x=3y+10$.
Substitute this into the second equation to get,
$(3y+10)-7y+30=0$,
Or, $4y=40$,
Or, $y=10$.
Substitute this value of $y$ into the expression for $x$,
$x=3y+10=30+10=40$.
Solution is, Jacob and his son't present ages are respectively 40 years and 10 years.
In the fourth part next, we'll learn another method of solving a pair of linear equations in two variables.
NCERT Solutions for Class 10 Maths
Chapter 1: Real Numbers
NCERT Solutions for Class 10 Maths on Real numbers part 1, Euclid’s division lemma puzzle solutions
Chapter 2: Polynomials
Chapter 3: Linear Equations
NCERT solutions for class 10 maths Chapter 3 Linear equations 7 Problem Collection
NCERT solutions for class 10 maths Chapter 3 Linear equations 6 Reducing non-linear to linear form
NCERT solutions for class 10 maths Chapter 3 Linear Equations 4 Algebraic solution by Elimination
NCERT solutions for class 10 maths Chapter 3 Linear Equations 3 Algebraic solution by Substitution
NCERT solutions for class 10 maths Chapter 3 Linear Equations 2 Graphical solutions
NCERT solutions for class 10 maths Chapter 3 Linear Equations 1 Graphical representation.
Chapter 4: Quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 1 What are quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 2 Solving by factorization
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 3 Solution by Completing the square
Chapter 6: Triangles
NCERT solutions for class 10 maths chapter 6 Triangles 1 Similarity of Triangles and Polygons
Solutions to Exercise 2 Chapter 6 NCERT X Maths, Characteristics of Similar triangles
Chapter 8: Introduction to Trigonometry, Concepts and solutions to exercise problems
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 1 Trigonometric Ratios
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 4 Trigonometric identities
Chapter 8: Introduction to Trigonometry, only solutions to selected problems
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 6
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 5
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 4
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 3
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 2
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 1