Solving a pair of non-linear equations by reducing method class 10
Reducing method enables conversion of a pair of non-linear equations to linear form and solve by a suitable method. NCERT Ex. 3.6 Class 10 solved.
We'll explain,
- Reducing method Class 10: how to solve a pair of non-linear equations in two variables reducing to linear form and then solve the linear equations by a suitable method.
- Under what conditions you can use the reducing method for solving a pair of non-linear equations in two variables, and,
- Solution to NCERT maths exercise 3.6 class 10 Reducing method.
You may move directly to any of the above sections by clicking its link and return by clicking on browser back button.
Reducing method Class 10: Solving a pair of non-linear equations by reducing to linear equations in Two Variables
We will solve two problems involving equations that are not linear, by reducing the equations to linear form using dummy variable substitution.
Example problem 1.
Find the value of $x$ and $y$ by solving the following pair of equations algebraically.
$\displaystyle\frac{2}{x}-\displaystyle\frac{3}{y}=\displaystyle\frac{4}{7}$ and $\displaystyle\frac{5}{x}+\displaystyle\frac{7}{y}=\displaystyle\frac{7}{2}$.
Solution to example problem 1—algebraic solution of two non-linear equations in two variables by reducing the equations to linear form with dummy variable substitution
The two equations are,
$\displaystyle\frac{2}{x}-\displaystyle\frac{3}{y}=\displaystyle\frac{4}{7}$ and,
$\displaystyle\frac{5}{x}+\displaystyle\frac{7}{y}=\displaystyle\frac{7}{2}$.
The two equations seem to be strange, involving inverse of $x$ and $y$.
This form of equations are classified as non-linear equations as the power of the standalone variable terms are not 1. In this case both powers are $(-1)$.
Obviously, you cannot use any of the methods you have learned till now for solving this pair of equations directly.
Innovative method
This is where the innovative method of solving this type of equations by reducing to linear form with dummy variable substitution is used.
Observe the key pattern in the two equations:
$\displaystyle\frac{1}{x}$ and $\displaystyle\frac{1}{y}$ appear in both equations and these are independent of each other.
As if these two expressions behave like two independent variables.
At this point you see the possibility—why not replace each of these two expressions by a distinct variable!
You decide to substitute dummy variables (to be used temporarily),
$p=\displaystyle\frac{1}{x}$, and
$q=\displaystyle\frac{1}{y}$.
And the two equations are immediately transformed by these substitutions to,
$2p-3q=\displaystyle\frac{4}{7}$ and,
$5p+7q=\displaystyle\frac{7}{2}$.
Now you have two equations in $p$ and $q$ that are linear and you know more than one method to solve such a pair of linear equations.
If a unique solution to this pair of equations exists, by solving the equations you would get the values of $p$ and $q$ and hence of $x$ and $y$.
- Excluding graphical method, you may use any of the other methods to solve the pair of linear equations in $p$ and $q$.
As we consider the method of elimination by fraction multiplier the quickest with least number of steps, we'll adopt this method.
Identifying the simplest term $2p$ to eliminate, multiply the first equation by $\displaystyle\frac{5}{2}$. Result is,
$5p-\displaystyle\frac{15}{2}q=\displaystyle\frac{10}{7}$.
Subtract this result from the second equation to eliminate $p$. Result is,
$\displaystyle\frac{29}{2}q=\displaystyle\frac{7}{2}-\displaystyle\frac{10}{7}=\displaystyle\frac{29}{14}$,
Or, $q=\displaystyle\frac{1}{7}=\frac{1}{y}$.
So, $y=7$.
Substitute the value of $q$ in first equation, $2p-3q=\displaystyle\frac{4}{7}$ to get,
$2p-\displaystyle\frac{3}{7}=\displaystyle\frac{4}{7}$,
Or, $2p=1$,
Or, $p=\displaystyle\frac{1}{2}=\frac{1}{x}$.
So, $x=2$.
Answer: $x=2$, $y=7$.
Verification: Substitute these two values in the given equations
$1-\displaystyle\frac{3}{7}=\displaystyle\frac{4}{7}$, and
$\displaystyle\frac{5}{2}+1=\displaystyle\frac{7}{2}$.
Solution verified.
Reducing method Class 10: Conditions under which a pair of non-linear equations can be reduced to linear form
Let us specify the conditions under which you can apply this novel method of solving two non-linear equations by expression substitution with dummy variables.
To solve two non-linear equations in two variables by reducing to linear forms, you must be able to present the equations in terms of two expressions that,
- Appear in the same form in both the equations. For example, you would be able to reduce to linear form two equations in $x$ and $y$ expressed in terms of $\displaystyle\frac{1}{x}$ and $\displaystyle\frac{1}{y}$ that appear in both equations,
- Are inherently linear when inverted if originally inverted. For example, $(x+y)$ is linear when appearing originally in both the equations as $\displaystyle\frac{1}{x+y}$, and
- Appear unrelated to and independent of each other (not as a product or division). For example, in case any $xy$ or $\displaystyle\frac{x}{y}$ is present in any of the two equations, the equations can't be reduced to linear form by dummy variable substitution.
In the problem we have just solved, the two given equations were in terms of expressions $\displaystyle\frac{1}{x}$ and $\displaystyle\frac{1}{y}$.
The two expressions are linear in $x$ and $y$ when inverted, appear unchanged in both equations and appear independently not as a product or division.
Let us solve a second problem to consolidate the new concept.
Example Problem 2: Two stage solution problem
Find the value of $x$ and $y$ by solving the following pair of equations algebraically.
$\displaystyle\frac{3}{3x+5y}-\displaystyle\frac{11}{x+2y}=-\displaystyle\frac{9}{10}$ and $\displaystyle\frac{5}{3x+5y}+\displaystyle\frac{1}{x+2y}=\displaystyle\frac{17}{66}$.
Solution to Example Problem 2—Solution of a pair non-linear equations by reducing to linear form with dummy variable substitution: First stage
The two equations are in terms of two expressions $\displaystyle\frac{1}{3x+5y}$ and $\displaystyle\frac{1}{x+2y}$ both of which satisfy the conditions for the equations to be reducible to linear form.
Substitute dummy variables $p$ and $q$ for these two denominator expressions,
$p=\displaystyle\frac{1}{3x+5y}$, and,
$q=\displaystyle\frac{1}{x+2y}$.
The two given equations are transformed to,
$3p-11q=-\displaystyle\frac{9}{10}$, and
$5p+q=\displaystyle\frac{17}{66}$.
Decide variable $q$ to be eliminated by multiplying the second equation with 11 and adding the result to the first equation. As a result of multiplication by 11 the second equation is changed to,
$55p+11q=\displaystyle\frac{17}{6}$.
Add it to the first equation to eliminate $q$. The result is,
$58p=\displaystyle\frac{17}{6}-\displaystyle\frac{9}{10}=\displaystyle\frac{58}{30}$,
Or, $p=\displaystyle\frac{1}{30}=\displaystyle\frac{1}{3x+5y}$.
So, $3x+5y=30$.............(1)
Substitute value of $p$ in first equation. Result is,
$\displaystyle\frac{1}{10}-11q=-\displaystyle\frac{9}{10}$,
Or, $11q=\displaystyle\frac{1}{10}+\displaystyle\frac{9}{10}=1$,
Or, $q=\displaystyle\frac{1}{11}=\frac{1}{x+2y}$.
So, $x+2y=11$............(2)
Solution to example problem 2: Second stage of solving two linear equations in $x$ and $y$
You have now two linear equations in $x$ and $y$ not in inverted form and easy to solve,
$3x+5y=30$, and
$x+2y=11$.
Multiply the second equation by 3 to get,
$3x+6y=33$.
Subtract first equation from this result to get,
$y=3$.
Substitute value of $y$ in the second equation. Result is,
$x+6=11$,
Or, $x=5$.
Answer: $x=5$, $y=3$.
Verification: Substitute these two values in the original two equations
$\displaystyle\frac{3}{30}-1=\displaystyle\frac{1}{10}-1=-\displaystyle\frac{9}{10}$, and
$\displaystyle\frac{5}{30}+\displaystyle\frac{1}{11}=\displaystyle\frac{1}{6}+\displaystyle\frac{1}{11}=\displaystyle\frac{17}{66}$.
Solution verified.
Note: In this problem two expressions both in $x$ and $y$ appeared unchanged in inverted form in the two given equations. So we could substitute dummy variables for these two expressions.
When you evaluated the dummy variables, you obtained a second pair of equations in $x$ and $y$ but this time in linear form.
This is a two-stage solution problem, and so is a little more difficult than the first example problem.
We'll now solve the problems in the exercise 3.6.
Solution to NCERT maths exercise 3.6 class 10 Reducing method
Problem 1.
Solve the following pairs of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{1}{2x}+\displaystyle\frac{1}{3y}=2$ and $\displaystyle\frac{1}{3x}+\displaystyle\frac{1}{2y}=\displaystyle\frac{13}{6}$
- $\displaystyle\frac{2}{\sqrt{x}}+\displaystyle\frac{3}{\sqrt{y}}=2$ and $\displaystyle\frac{4}{\sqrt{x}}-\displaystyle\frac{9}{\sqrt{y}}=-1$
- $\displaystyle\frac{4}{x}+3y=14$ and $\displaystyle\frac{3}{x}-4y=23$
- $\displaystyle\frac{5}{x-1}+\displaystyle\frac{1}{y-2}=2$ and $\displaystyle\frac{6}{x-1}-\displaystyle\frac{3}{y-2}=1$
- $\displaystyle\frac{7x-2y}{xy}=5$ and $\displaystyle\frac{8x+7y}{xy}=15$
- $6x+3y=6xy$ and $2x+4y=5xy$
- $\displaystyle\frac{10}{x+y}+\displaystyle\frac{2}{x-y}=4$ and $\displaystyle\frac{15}{x+y}-\displaystyle\frac{5}{x-y}=-2$
- $\displaystyle\frac{1}{3x+y}+\displaystyle\frac{1}{3x-y}=\displaystyle\frac{3}{4}$ and $\displaystyle\frac{1}{2(3x+y)}-\displaystyle\frac{1}{2(3x-y)}=\displaystyle\frac{-1}{8}$
Problem 2.
Formulate the following problems as a pair of equations, and hence find their solutions.
- Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of current.
- 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
- Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution to the problems
Problem 1.i.
Solve the following pair of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{1}{2x}+\displaystyle\frac{1}{3y}=2$ and $\displaystyle\frac{1}{3x}+\displaystyle\frac{1}{2y}=\displaystyle\frac{13}{6}$
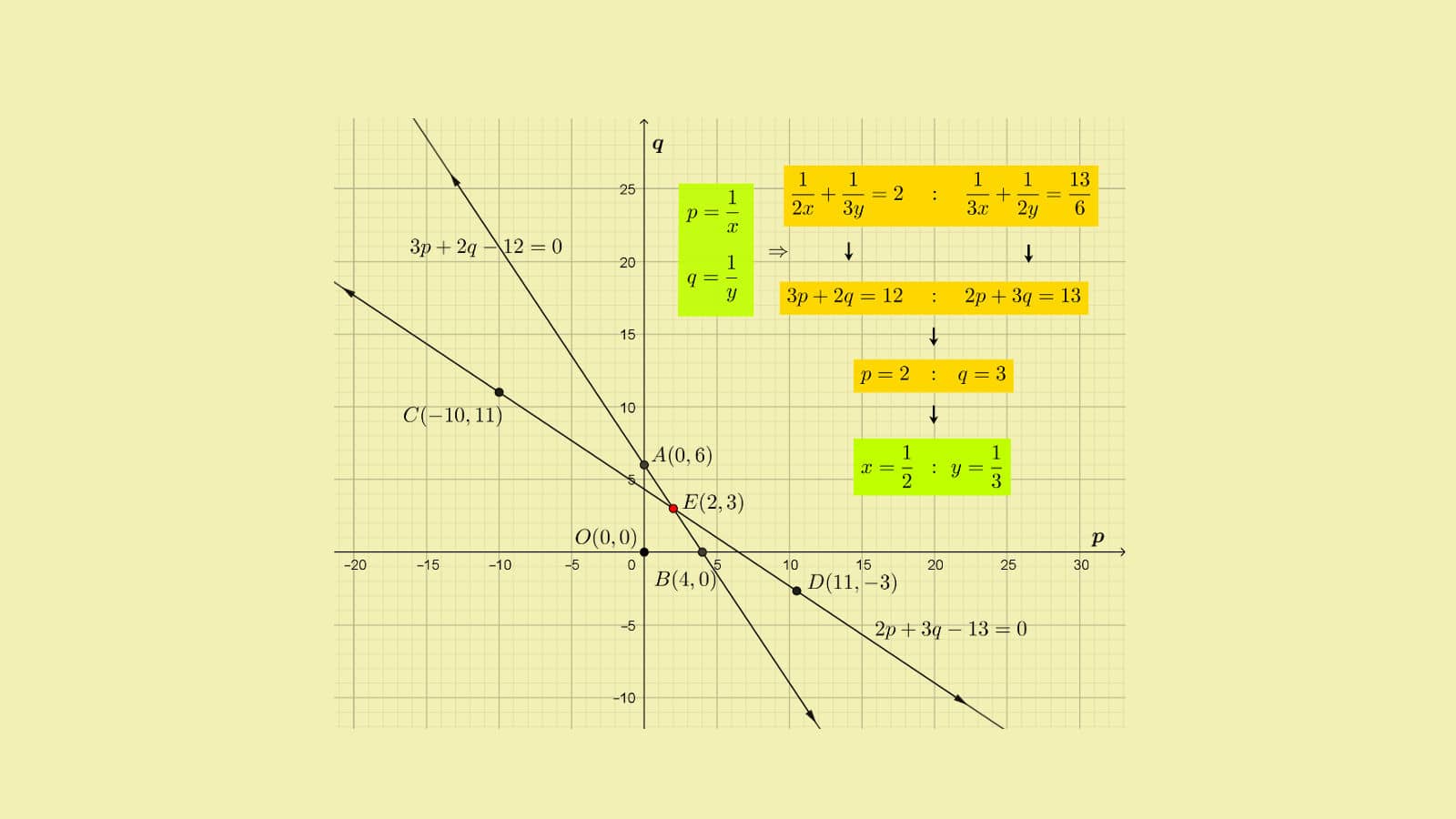
Solution to Problem 1.i: First stage: Reduction of the pair of equations to a pair of linear equations by suitable expression substitution with dummy variables
The two equations are,
$\displaystyle\frac{1}{2x}+\displaystyle\frac{1}{3y}=2$ and,
$\displaystyle\frac{1}{3x}+\displaystyle\frac{1}{2y}=\displaystyle\frac{13}{6}$.
As the primary variables $x$ and $y$ are in inverses, the pair of equations are non-linear.
It is difficult to plot the two graphs for the two given equations let alone find a solution. So what do we do?
Pattern discovery: This is the point when you discover the pattern that both $\displaystyle\frac{1}{x}$ and $\displaystyle\frac{1}{y}$ appear in the two equations independently and in unchanged form.
As if each of the two are independent of each other in both the equations.
So you can substitute one new variable say, $p$ for $\displaystyle\frac{1}{x}$ and a second new variable $q$ for $\displaystyle\frac{1}{y}$. These are dummy variables to be used temporarily.
With these substitutions, the given equations are transformed to linear forms,
$\frac{1}{2}p+\frac{1}{3}q=2$,
Or, $3p+2q=12$, multiplying both equations by 6 to eliminate fraction coefficients, and
$\frac{1}{3}p+\frac{1}{2}q=\displaystyle\frac{13}{6}$,
Or, $2p+3q=13$, again multiplying both equations by 6 to eliminate fraction coefficients.
Now you have two linear equations in two variables $p$ and $q$. Don't worry about $x$ and $y$. Those are hidden in $p$ and $q$. You can find the values of $p$ and $q$ easily and then of $x$ and $y$ also.
You may solve the two equations by any of the methods you are comfortable with.
Let us see the graphical view by plotting the two equations in $p-q$ coordinate axes with values of $p$ plotted along the horizontal axis and values of $q$ on the vertical axis,

Using the method of elimination by fraction multiplier we choose to multiply the first equation by $\displaystyle\frac{3}{2}$ to eliminate $q$. First equation is changed to,
$\displaystyle\frac{9}{2}p+3q=18$.
Subtract the second equation from this transformed equation. Result is,
So, $\displaystyle\frac{5}{2}p=5$,
Or, $p=2$.
So, $x=\displaystyle\frac{1}{p}=\frac{1}{2}$.
Substitute $p=2$ in the first equation, $3p+2q=12$. Result is,
$2q=6$,
Or, $q=3$.
So, $y=\displaystyle\frac{1}{q}=\frac{1}{3}$.
Answer: $x=\displaystyle\frac{1}{2}$ and, $y=\displaystyle\frac{1}{3}$.
Verification: Substitute these values of $x$ and $y$ in the original two equations. Results are,
$1+1=2$, and,
$\displaystyle\frac{2}{3}+\displaystyle\frac{3}{2}=\displaystyle\frac{13}{6}$. Solution verified as correct.
Problem 1.ii.
Solve the following pair of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{2}{\sqrt{x}}+\displaystyle\frac{3}{\sqrt{y}}=2$ and $\displaystyle\frac{4}{\sqrt{x}}-\displaystyle\frac{9}{\sqrt{y}}=-1$
Solution to Problem 1.ii: Solution of two non-linear equations by suitable dummy variable substitution and solving the two transformed linear equations
The two equations being non-linear and the causes of non-linearity—the expressions, $\displaystyle\frac{1}{\sqrt{x}}$ and $\displaystyle\frac{1}{\sqrt{y}}$ both appearing independently and in unchanged form in the two equations, we can always substitute dummy variables $p$ and $q$ for these two expessions to transform the two equations to a pair of linear equations in $p$ and $q$,
$p=\displaystyle\frac{1}{\sqrt{x}}$, and
$q=\displaystyle\frac{1}{\sqrt{y}}$.
As a result, the two given equations are transformed to,
$2p+3q=2$ and,
$4p-9q=-1$.
You can solve this pair of linear equations in two variables by any of the methods that you are comfortable with.
As far as we are concerned,
In most cases we adopt elimination method, and when needed we use fraction multiplier.
In this case we would eliminate $p$ by just multiplying first equation by 2 and then subtracting the second equation from the transformed first equation. Result of multiplication is,
$4p+6q=4$.
Subtract the second equation from this transformed equation to eliminate $p$. Result is,
$15q=5$,
Or, $q=\displaystyle\frac{1}{3}=\frac{1}{\sqrt{y}}$.
So, $y=9$.
Substitute value of $q=\displaystyle\frac{1}{3}$ in the simpler first equation, $2p+3q=2$. Result is,
$2p=1$,
Or, $p=\displaystyle\frac{1}{2}=\frac{1}{\sqrt{x}}$.
So, $x=4$.
Answer: $x=4$, and $y=9$.
Verification: Substitute the values of $x$ and $y$ in the two equations to get respectively,
$1+1=2$, and
$2-3=-1$.
The values satisfy both the equations and so is the correct solution.
Problem 1.iii.
Solve the following pair of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{4}{x}+3y=14$ and $\displaystyle\frac{3}{x}-4y=23$
Solution to Problem 1.iii: Reducing non-linear equations to linear by single dummy variable substitution
In this problem you need to replace only the single offending expression, $\displaystyle\frac{1}{x}$ that is causing non-linearity in both the equations, by dummy variable $p$ to transform the two equations into a pair of linear equations in $p$ and $y$ and then solve for $p$ and $y$.
So substitute,
$p=\displaystyle\frac{1}{x}$
The two transformed equations become,
$4p+3y=14$, and
$3p-4y=23$.
You may eliminate $p$ by multiplying first equation by 3, second by 4 and subtracting the second from the first results. That's a lot of calculation for us.
Instead, we like to use the fraction multiplier of $\displaystyle\frac{3}{4}$ multiplied through the first equation thus transforming it to,
$3p+\displaystyle\frac{9}{4}y=\displaystyle\frac{21}{2}$.
Subtract second equation from this result to get,
$\displaystyle\frac{25}{4}y=-\displaystyle\frac{25}{2}$,
Or, $y=-2$.
Substituting this value into the second equation you get,
$3p+8=23$,
Or, $3p=15$,
Or, $p=5=\displaystyle\frac{1}{x}$.
So, $x=\displaystyle\frac{1}{5}$.
Answer: $x=\displaystyle\frac{1}{5}$ and $y=-2$.
Verification: Substitute these two values into the two given equations to get,
$20-6=14$, and
$15+8=23$. Solution verified as correct.
Problem 1.iv.
Solve the following pair of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{5}{x-1}+\displaystyle\frac{1}{y-2}=2$ and $\displaystyle\frac{6}{x-1}-\displaystyle\frac{3}{y-2}=1$
Solution to Problem 1.iv: Reducing non-linear equations to linear by expression substitution
In this case the two expressions causing non-linearity are,
$\displaystyle\frac{1}{x-1}$, and
$\displaystyle\frac{1}{y-2}$.
Both these expressions appear in the two equations independent of each other and in unchanged form. And so these two expressions can be replaced by any pair of temporary dummy variables,
$p=\displaystyle\frac{1}{x-1}$, and
$q=\displaystyle\frac{1}{y-2}$.
As a result of these substitutions, the two given equations are transformed to,
$5p+q=2$, and
$6p-3q=1$.
Eliminate $q$ first by simply multiplying only the first equation by 3 and then adding the two results.
As a result of multiplication by 3 the first equation is transformed to,
$15p+3q=6$.
Add this to the second equation. Result is,
$21p=7$,
Or, $p=\displaystyle\frac{7}{21}=\frac{1}{3}=\frac{1}{x-1}$,
Or, $x-1=3$,
Or, $x=4$.
Substitute value of $p$ in simpler equation, $5p+q=2$. Result is,
$q=2-\displaystyle\frac{5}{3}=\displaystyle\frac{1}{3}=\displaystyle\frac{1}{y-2}$
Or, $y-2=3$,
So, $y=5$.
Answer: $x=4$ and $y=5$.
Verification: Substitute these two values to the first and second given equation respectively to get,
$\displaystyle\frac{5}{3}+\displaystyle\frac{1}{3}=2$, and
$\displaystyle\frac{6}{3}-\displaystyle\frac{3}{3}=1$.
Solution verified.
Problem 1.v.
Solve the following pairs of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{7x-2y}{xy}=5$ and $\displaystyle\frac{8x+7y}{xy}=15$
Solution to Problem 1.v: Transforming non-linear equations to suitable form for reduction to linear equations
This is a more complex problem because the two expressions causing non-linearity and appearing independent of each other and in unchanged form cannot be readily identified.
You need to transform the two equations first by algebraic simplification.
Just carry out the division of each term by existing denominator $xy$. Simplified results are,
$\displaystyle\frac{7}{y}-\displaystyle\frac{2}{x}=5$, and
$\displaystyle\frac{8}{y}+\displaystyle\frac{7}{x}=15$.
Now you can identify the two expressions $\displaystyle\frac{1}{y}$ and $\displaystyle\frac{1}{x}$ that appear independent of each other and in unchanged form in both the two transformed equations.
Replace these two expressions respectively by temporary dummy variables $p$ and $q$ respectively,
$p=\displaystyle\frac{1}{y}$ and,
$q=\displaystyle\frac{1}{x}$.
By these two substitutions the two given equations are transformed to the linear forms of,
$7p-2q=5$, and
$8p+7q=15$.
You may adopt any of the methods that you are comfortable with.
For us, we always go for elimination method, and whenever required—elimination by fraction multiplier.
If any of the four coefficients of the two variables in two equations are either 2 or 5, fraction manipulation is the simplest. You may even carry out the calculations easily in decimals. That's what we look for.
Following this rule we identify, $(-2q)$ as the convenient term so that by multiplying the first equation by $\displaystyle\frac{7}{2}$ this term is transformed to just $(-7q)$ so that when this transformed equation is added to the second equation, the two terms in $q$ are cancelled out.
Accordingly, by the multplication thought out, the first equation is transformed to,
$\displaystyle\frac{49}{2}p-7q=\displaystyle\frac{35}{2}$.
Add this result with the second equation. Result of addition is,
$\left(\displaystyle\frac{49}{2}+8\right)p=\displaystyle\frac{35}{2}+15$,
Or, $\displaystyle\frac{65}{2}p=\frac{65}{2}$,
Or, $p=1=\displaystyle\frac{1}{y}$.
So, $y=1$.
Substitute value of $p$ in first unchanged simpler equation, $7p-2q=5$ and get,
$7-2q=5$,
Or, $q=1=\displaystyle\frac{1}{x}$,
So, $x=1$.
Answer: $x=1$, $y=1$.
Verification: Substitute these two values in the two given equations to get,
$7-2=5$, and
$8+7=15$.
Solution verified.
Problem 1.vi.
Solve the following pair of equations by reducing them to a pair of linear equations.
- $6x+3y=6xy$ and $2x+4y=5xy$
Solution to Problem 1.vi: Solution of non-linear equations by Expression elimination using Abstraction
Again you identify the key pattern to simplify the two equations first by dividing first equation throughout by $3xy$ and the second by $xy$ to get,
$\displaystyle\frac{2}{y}+\displaystyle\frac{1}{x}=2$, and
$\displaystyle\frac{2}{y}+\displaystyle\frac{4}{x}=5$.
Implicit abstraction and solution by no conversion
You may follow the method of dummy variable subtitution and convert the two non-linear equations to linear form first.
But this time we would show you a faster and more abstract method in which we'll get the value of $\displaystyle\frac{1}{x}$ directly without any substitution by subtracting the first equation from the second.
This action we identify as the easiest approach based on the pattern discovery of first terms of both equations as equal.
Recommendation: Do not always follow a method of problem solving mechanically—always look out for useful pattern in the problem that can be used for solving the problem faster and easier in minimum number of steps.
In fact, the dummy variable substitution method itself is the result of presence of a specific pattrern in the two equations.
As thought out, the result of subtraction of the first equation from the second is,
$\displaystyle\frac{3}{x}=3$,
Or, $x=1$.
Substitute this value in the first simpler equation to get,
$y=2$.
Answer: $x=1$, and $y=2$.
Verification: Substitute these values in the two given equations to get,
$6+6=6\times{2}=12$, and
$2+4\times{2}=2+8=5\times{2}=10$.
Solution verified.
Solution of two non-linear equations in two variables by Expression Elimination
What did we actually do to solve the two equations in this problem?
Effectively we have eliminated a variable expression $\displaystyle\frac{1}{y}$ from the two equations bypassing conversion to linear form and then solving for values of $x$ and $y$.
The necessary conditions for eliminating one variable expression from two equations directly are same as the conditions for conversion of the equations to linear form by suitable dummy variable substitution and then solution. These conditions are explained while solving the example problem 1.
If these conditions are satisfied, you can replace each such expression by a compound dummy variable (compound because it will represent an expression) and the result will be two linear equations in two dummy variables.
And so, without going through substitution, under such conditions you can directly eliminate one of the two expressions from the two non-linear equations in two elementary variables.
Finally then we may generalize this specially powerful method of transformation and simplification of nature of the equations before solving them as, Solving two non-linear equations by Expression Elimination.
This is the method we followed in solving this problem. Result? Nearly instantaneous solution in minimum number of steps with mathematical rigor.
For your benefit we'll show you the conventional method of solving this problem by reducing the two equations to linear form first.
Conventional Solution to Problem 1.vi: Reducing the equations to linear form first
The two equations are,
$6x+3y=6xy$ and,
$2x+4y=5xy$.
Simplify the equations by dividing the first equation with $3xy$ and the second with $xy$ to get,
$\displaystyle\frac{2}{y}+\displaystyle\frac{1}{x}=2$, and
$\displaystyle\frac{2}{y}+\displaystyle\frac{4}{x}=5$.
Substitute dummy variables,
$p=\displaystyle\frac{1}{y}$, and,
$q=\displaystyle\frac{1}{x}$.
Resulting transformed equations are,
$2p+q=2$, and,
$2p+4q=5$.
Subtract first equation from second to eliminate $q$. Result of subtraction is,
$3q=3$.
Or, $q=1=\displaystyle\frac{1}{x}$,
Or, $x=1$.
Substitute value of $q$ in simpler first equation. Result is,
$2p+1=2$,
Or, $p=\displaystyle\frac{1}{2}=\frac{1}{y}$,
Or, $y=2$.
Answer: $x=1$, $y=2$. Same as before, but in a few extra steps.
Problem 1.vii:
Solve the following pair of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{10}{x+y}+\displaystyle\frac{2}{x-y}=4$ and $\displaystyle\frac{15}{x+y}-\displaystyle\frac{5}{x-y}=-2$
Solution to Problem 1.vii: Reducing a pair of non-linear equations to linear by expression substitution
This time the consistently appearing two expressions are, $\displaystyle\frac{1}{(x+y)}$ and $\displaystyle\frac{1}{(x-y)}$.
Replace the two by dummy variables $p$ and $q$ respectively,
$p=\displaystyle\frac{1}{x+y}$, and
$q=\displaystyle\frac{1}{x-y}$.
The transformed equations become,
$10p+2q=4$,
Or, $5p+q=2$, eliminating common factor 2, and
$15p-5q=-2$.
We can eliminate either $p$ or $q$ by changing a single equation. Let us decide to change the first equation by multiplying with 5 getting,
$25q+5q=10$.
Add this result to the second equation to cancel out the terms in $q$. Result is,
$40p=8$,
Or, $p=\displaystyle\frac{1}{5}=\displaystyle\frac{1}{x+y}$,
Or, $x+y=5$.
Substituting value of $p$ into first equation, $5p+q=2$ to get,
$1+q=2$,
Or, $q=1=\displaystyle\frac{1}{x-y}$,
Or, $x-y=1$.
Add the values of $(x+y)=5$, and $(x-y)=1$. Result is,
$2x=6$,
Or, $x=3$.
Substitute this value in first equation,
$x+y=3+y=5$,
Or, $y=2$.
Answer: $x=3$ and $y=2$.
Verification: Substitutre these two values directly in the two given equations to get,
$\displaystyle\frac{10}{5}+\displaystyle\frac{2}{1}=4$, and
$\displaystyle\frac{15}{5}-\displaystyle\frac{5}{1}=3-5=-2$.
Solution verified.
Problem 1.viii.
Solve the following pairs of equations by reducing them to a pair of linear equations.
- $\displaystyle\frac{1}{3x+y}+\displaystyle\frac{1}{3x-y}=\displaystyle\frac{3}{4}$ and $\displaystyle\frac{1}{2(3x+y)}-\displaystyle\frac{1}{2(3x-y)}=\displaystyle\frac{-1}{8}$
Solution to Problem 1.viii: Reducing a pair of non-linear equations to linear by expression substitution with dummy variables
Identify the key pattern that the expressions $\displaystyle\frac{1}{3x+y}$ and $\displaystyle\frac{1}{3x-y}$ are the two expressions that appear unchanged in both the equations. So we decide to substitute dummy variables $p$ and $q$ for these two expressions respectively,
$p=\displaystyle\frac{1}{3x+y}$, and,
$q=\displaystyle\frac{1}{3x-y}$.
By these two substitutions the equations are transformed to linear forms,
$p+q=\displaystyle\frac{3}{4}$, and
$\displaystyle\frac{p}{2}-\displaystyle\frac{q}{2}=\displaystyle\frac{-1}{8}$,
Or, $p-q=\displaystyle\frac{-1}{4}$.
Adding this result with the first transformed equation you get,
$2p=\displaystyle\frac{2}{4}=\frac{1}{2}$,
Or, $p=\displaystyle\frac{1}{4}=\displaystyle\frac{1}{3x+y}$,
Or, $3x+y=4$.
Substituting value of $p$ into the first equation you get,
$p+q=\displaystyle\frac{1}{4}+q=\displaystyle\frac{3}{4}$,
Or, $q=\displaystyle\frac{2}{4}=\frac{1}{2}=\frac{1}{3x-y}$,
Or, $3x-y=2$.
Adding the two,
$6x=6$,
Or, $x=1$.
Substituting in $(3x+y)=4$,
$3+y=4$,
Or, $y=1$.
Answer: $x=1$, $y=1$.
Verification: Substitute these two values into the two given equations to get,
$\displaystyle\frac{1}{4}+\displaystyle\frac{1}{2}=\displaystyle\frac{3}{4}$, and
$\displaystyle\frac{1}{8} -\displaystyle\frac{1}{4}=\displaystyle\frac{-1}{8}$.
Solution verified.
Problem 2.i.
Formulate the following problem as a pair of equations, and hence find the solution.
- Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of current.
Solution to Problem 2.i: By Boats and streams concepts and reducing a pair of non-linear equations to linear
Assume the speeds of Ritu rowing in still water and the speed of stream current as $x$ and $y$ respectively in km per hour.
Concepts on Boats and Streams
When a rower rows upstream, the rower moves slowly because the stream current flowing in opposite direction opposes the movement of the rower.
In other words, effective relative upstream speed of the rower beomes,
$x-y$.
On the other hand when the rower rows downstream along the same direction of the stream, the stream flow aids the rower and carries her forward faster.
In other words, the effective relative downstream speed of the rower becomes,
$x+y$.
You may have a question regarding the reference point of these relative speeds.
A person standing on any of the two stream banks parallel to the direction of rowing (and stream current) will see the rower moving at these relative speeds.
Lastly, by the concepts of speed, time and distance,
$\text{Distance covered }=\text{ Speed }\times{\text{ Time}}$.
Applying these concepts form the two equations from the problem statements as,
$2(x+y)=20$,
Or, $x+y=10$, always eliminate the factor common between the terms, and
$2(x-y)=4$,
Or, $x-y=2$.
Add the two equations to eliminate $y$,
$2x=12$,
Or, $x=6$.
Substitute in $(x+y)=10$,
$6+y=10$,
Or, $y=4$.
Answer: Still water speed of rowing of Ritu is 6 km per hour and the stream current speed is 4 km per hour.
Verification: Substitute these values in the original two equations,
$2(x+y)=2\times{10}=20$, and
$2(x-y)=2\times{2}=4$.
Solution verified.
Problem 2.ii.
Formulate the following problem as a pair of equations, and hence find the solution.
- 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
Solution to Problem 2.ii: Work time concepts and reducing non-linear equations to linear form
Let us assume a woman completes the total work in $w$ days and a man completes the same work in $m$ days.
So, in 1 day, a woman completes $\displaystyle\frac{1}{w}$ portion of total work and a man completes $\displaystyle\frac{1}{m}$ portion of total work.
By the first statement 2 women and 5 men finish an embroidery work in 4 days. This relation may then be expressed as,
$4\times{\left(\displaystyle\frac{2}{w}+\displaystyle\frac{5}{m}\right)}=1$, where 1 represents the whole amount of work.
Or, $\displaystyle\frac{2}{w}+\displaystyle\frac{5}{m}=\displaystyle\frac{1}{4}$.
That is, in 1 day one-fourth of the total work is completed by 2 women and 5 men working together. This makes sense as work portion completed is directly proportional to number of days of work, other things remaining unchanged.
Similarly the second statement may be represented by the relation,
$3\times{\left(\displaystyle\frac{3}{w}+\displaystyle\frac{5}{m}\right)}=1$.
Or, $\displaystyle\frac{3}{w}+\displaystyle\frac{6}{m}=\displaystyle\frac{1}{3}$.
We have then two non-linear equations in two variables $w$ and $m$.
The causes of non-linearity are $\displaystyle\frac{1}{w}$ and $\displaystyle\frac{1}{m}$.
Substitute dummy variables for these two expressions as,
$p=\displaystyle\frac{1}{w}$, and
$q=\displaystyle\frac{1}{m}$.
The two equations are changed to a pair of linear equations in $p$ and $q$ as,
$2p+5q=\displaystyle\frac{1}{4}$, and
$3p+6q=\displaystyle\frac{1}{3}$.
You may solve these two equations adopting the method you are comfortable in.
We invariably use in this type of problems, the method of elimination using fraction multiplier.
Multiply the first equation by $\displaystyle\frac{3}{2}$ intending to eliminate $p$. The result of multiplication is,
$3p+\displaystyle\frac{15}{2}q=\displaystyle\frac{3}{8}$.
Subtract the second equation from this result and eliminate $p$. Result is,
$q\left(\displaystyle\frac{15}{2}-6\right)=\displaystyle\frac{3}{8}-\displaystyle\frac{1}{3}$,
Or, $\displaystyle\frac{3}{2}q=\displaystyle\frac{1}{24}$,
Or, $q=\displaystyle\frac{1}{36}=\displaystyle\frac{1}{m}$.
So, $m=36$.
Substitute value of $q$ in second equation. Result is,
$3p+\displaystyle\frac{1}{6}=\displaystyle\frac{1}{3}$,
Or, $3p=\displaystyle\frac{1}{3}-\displaystyle\frac{1}{6}=\displaystyle\frac{1}{6}$,
Or, $p=\displaystyle\frac{1}{18}=\frac{1}{w}$.
So, $w=18$.
Answer: 1 woman finishes the embroidery work while working alone in 18 days and a man alone finishes it in 36 days.
Verification: Substitute the values of $w$ and $m$ in the initial two equations. Results are,
$\displaystyle\frac{2}{18}+\displaystyle\frac{5}{36}=\displaystyle\frac{1}{4}$, and,
$\displaystyle\frac{3}{18}+\displaystyle\frac{6}{36}=\displaystyle\frac{1}{3}$.
Solution verified.
Problem 2.iii.
Formulate the following problem as a pair of equations, and hence find the solution.
- Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.
Solution to Problem 2.iii: Solution by Speed time distance concepts and reduction of non-linear equations to linear form
Let the speed of the train be $u$ and that of the bus be $v$ both in term of km per hour.
The first journey of 300 km is represented then by,
$\displaystyle\frac{60}{u}+\displaystyle\frac{240}{v}=4$, time of travel is distance divided by speed.
Eliminating factor 4 from the three terms,
$\displaystyle\frac{15}{u}+\displaystyle\frac{60}{v}=1$.
This is the first non-linear equation in $u$ and $v$.
Similarly the second journey of the same 300 km is represented by,
$\displaystyle\frac{100}{u}+\displaystyle\frac{200}{v}=4\frac{1}{6}=\displaystyle\frac{25}{6}$.
Again eliminate the common factor of 25 from three terms,
$\displaystyle\frac{4}{u}+\displaystyle\frac{8}{v}=\displaystyle\frac{1}{6}$.
This is the second non-linear equation in $u$ and $v$.
To convert the two equations to linear form, substitute dummy variables,
$p=\displaystyle\frac{1}{u}$ and,
$q=\displaystyle\frac{1}{v}$.
The two linear equations formed because of the substitutions are,
$15p+60q=1$, and
$4p+8q=\displaystyle\frac{1}{6}$,
Or, $2p+4q=\displaystyle\frac{1}{12}$, making elimination of $q$ easier.
Multiply second equation by 15. Resulting equation is,
$30p+60q=\displaystyle\frac{5}{4}$.
Subtract first equation from second to get,
$15p=\displaystyle\frac{1}{4}$,
Or, $p=\displaystyle\frac{1}{60}=\frac{1}{u}$.
So, $u=60$ km per hour.
Substitute value of $p$ in first equation. Result is,
$\displaystyle\frac{1}{4}+60q=1$,
Or, $60q=\displaystyle\frac{3}{4}$,
Or, $p=\displaystyle\frac{1}{80}=\frac{1}{v}$.
So, $v=80$ km per hour.
Answer: Speed of the train is 60 km per hour and the speed of the bus is 80 km per hour.
Verification: Substitute these two values in the two equations formed at the start.
The equation for the first journey of 300 km has been,
$\displaystyle\frac{60}{u}+\displaystyle\frac{240}{v}=4$,
Or, $\displaystyle\frac{60}{60}+\displaystyle\frac{240}{80}=1+3=4$. Relation satisfied.
The equation representing the second journey has been,
$\displaystyle\frac{100}{u}+\displaystyle\frac{200}{v}=\displaystyle\frac{25}{6}$,
Or, $\displaystyle\frac{100}{60}+\displaystyle\frac{200}{80}=\displaystyle\frac{5}{3}+\displaystyle\frac{5}{2}=\displaystyle\frac{25}{6}$. This relation is also satisfied and so the solution is verified.
Next in the seventh part, we'll learn how to solve a host of different types of problems based on a pair of linear equations.
NCERT Solutions for Class 10 Maths
Chapter 1: Real Numbers
NCERT Solutions for Class 10 Maths on Real numbers part 1, Euclid’s division lemma puzzle solutions
Chapter 2: Polynomials
Chapter 3: Linear Equations
NCERT solutions for class 10 maths Chapter 3 Linear equations 7 Problem Collection
NCERT solutions for class 10 maths Chapter 3 Linear equations 6 Reducing non-linear to linear form
NCERT solutions for class 10 maths Chapter 3 Linear Equations 4 Algebraic solution by Elimination
NCERT solutions for class 10 maths Chapter 3 Linear Equations 3 Algebraic solution by Substitution
NCERT solutions for class 10 maths Chapter 3 Linear Equations 2 Graphical solutions
NCERT solutions for class 10 maths Chapter 3 Linear Equations 1 Graphical representation.
Chapter 4: Quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 1 What are quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 2 Solving by factorization
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 3 Solution by Completing the square
Chapter 6: Triangles
NCERT solutions for class 10 maths chapter 6 Triangles 1 Similarity of Triangles and Polygons
Solutions to Exercise 2 Chapter 6 NCERT X Maths, Characteristics of Similar triangles
Chapter 8: Introduction to Trigonometry, Concepts and solutions to exercise problems
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 1 Trigonometric Ratios
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 4 Trigonometric identities
Chapter 8: Introduction to Trigonometry, only solutions to selected problems
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 6
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 5
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 4
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 3
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 2
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 1