Similarity of Triangles and Polygons - NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.1
In part 1 of NCERT Solutions for Class 10 Maths Chapter 6 Triangles we'll cover similarity of triangles and polygons and will solve the questions in Ex 6.1.
We'll cover now,
- What is similarity of shapes and triangles.
- Transitivity of similarity of triangles.
- When polygons with same number of equal sides are not similar.
- Conditions for a pair of polygons to be congruent.
- Solution to Exercise 6.1 NCERT Solutions class 10 maths on similarity of triangles and polygons.
You may move directly to any of the above sections by clicking its link and return by clicking on browser back button.
What is similarity of shapes and triangles
When in geometry we use the term similarity, it is used in a very specific way, not loosely or vaguely as in daily use of the word.
Similarity between two shapes, pictures or geometric shapes, is defined as,
Two shapes are technically similar when all line segments that together form the smaller shape are enlarged to form the larger shape so that,
1. Angle between any corresponding pair of line segments in the two shapes are equal, and,
2. Ratio of length of all corresponding pair of line segments of the two shapes are equal.
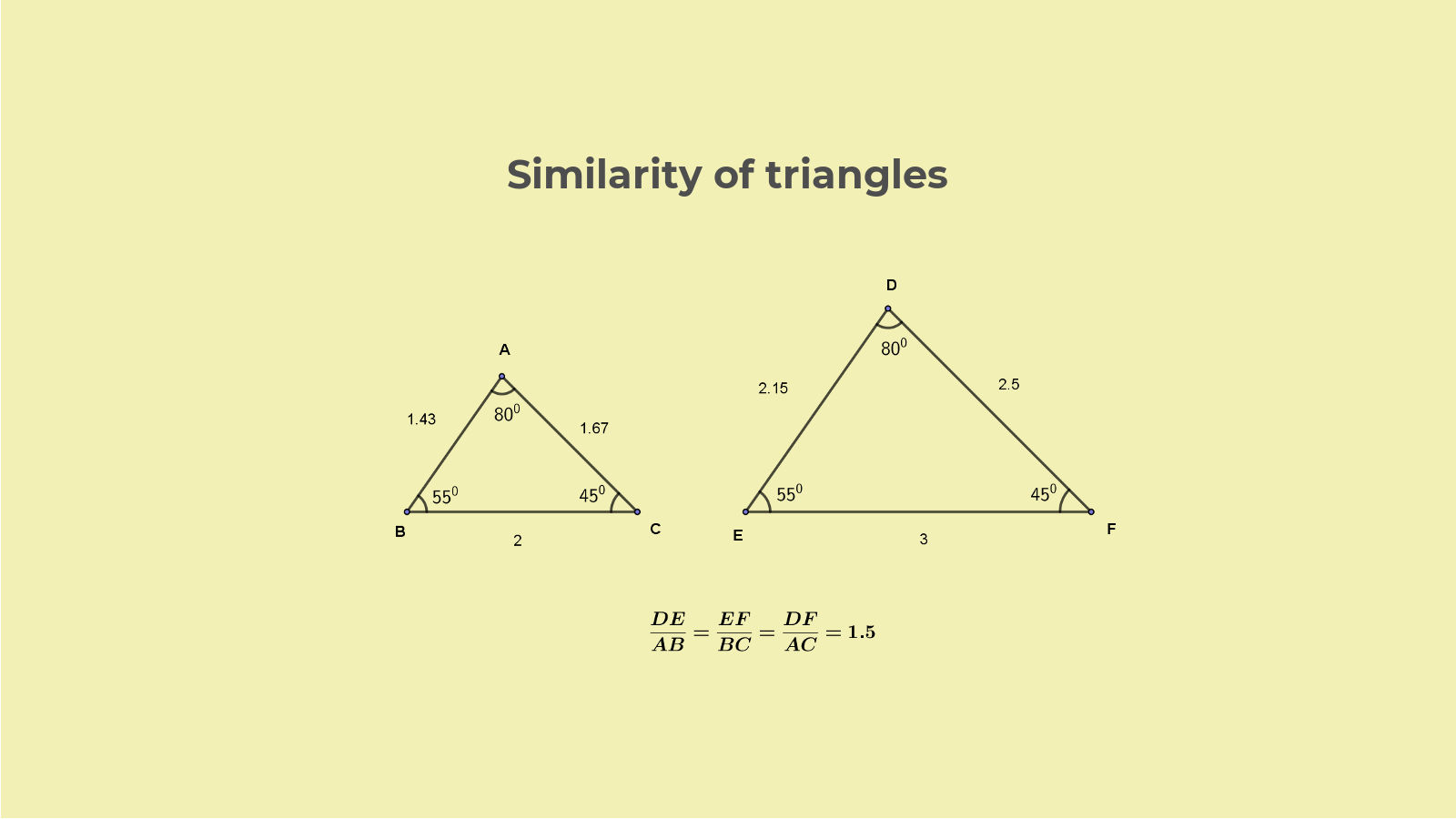
The concept is easy to appreciate from the following pair of similar triangles, $\triangle ABC$ and $\triangle DEF$.
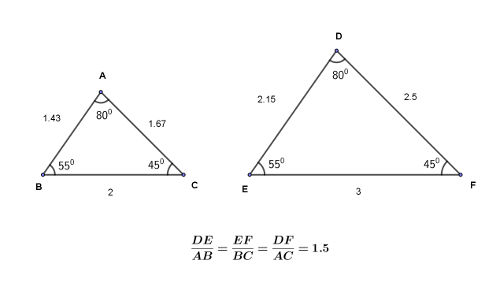
You can visually identify that the pair of sides AB, DE and also, BC, EF and AC, DF are corresponding pairs of sides of the two triangles. DE is just the longer version of AB and the same for EF, BC and DF, AC.
But how did you identify that?
First you identified that AB is inclined to BC in the same way that DE is inclined to EF. It meant, $\angle ABC=\angle DEF$. Similarly it has been easy to see that $\angle ACB=\angle DFE$, and $\angle BAC=\angle EDF$.
These are the corresponding pairs of angles in the two triangles that are equal.
This equality fulfilled the first condition of similarity of the two triangles.
And then you could also detect that AB and DE are corresponding pair of sides because, both are opposite to equal angles $\angle ACB=\angle EFD$.
Finally then it was easy to assess visually that EF and DF are larger than their corresponding sides BC and AC respectively by the same proportion as the proportion by which DE is larger than AB.
Mathematically this means, ratio of three corresponding pairs of sides in the two similar triangles are equal, that is,
$\displaystyle\frac{DE}{AB}=\frac{EF}{BC}=\frac{DF}{AC}$.
In the two similar triangles, both the conditions of similarity will be true. That you can assess visually for these two triangles, isn't it?
Thus, when two triangles are similar,
One is simply the enlarged version of the other.
Note: When a picture or photo is resized/resampled using a graphic software such as GIMP, the leading open source free graphic software, if the ASPECT RATIO (width to height ratio) is kept unchanged, the smaller picture becomes the exact replica of the original larger picture, except that it is smaller in size. These two form a pair of similar pictures. The following is an example,

Likewise, any two polygons with same number of sides will be similar if the two meet the pair of similarity conditions. Following shows a pair of similar triangles and a pair of similar quadrangles.
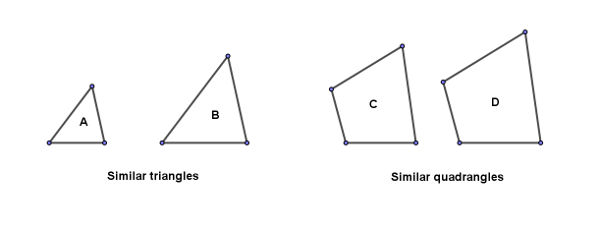
The two triangles A and B are similar, and the two quadrangles C and D are similar. Each pair of polygons meet the couple of similarity conditions between them.
Note that triangle A or triangle B cannot be similar to any of the quadrangles, simply because their number of sides are unequal.
Question of similarity of two polygons arise only between two polygons of same number of sides.
The property of similarity of triangles is transitive
By the property of transitivity we mean simply, if $A=B$ and $B=C$, then $B=C$. This example is for the property EQUALITY.
The same transitivity holds true for similarity also.
If two shapes (pictures, polygons or triangles) A and B as well as B and C are similar, then shape A must be similar to shape C.
You can verify this truth easily using mathematics as well as by visual assessment. In the following figure similarity of three triangles is shown highlighting the property of transitivity.

Mathematically we express the similarity of the three triangles as,
$\triangle ABC \sim \triangle DEF \sim \triangle PQR$.
Cases when two polygons with same number of equal sides are NOT similar to each other
Though we stated, in two similar shapes both the similarity conditions must be true, the fact is, FOR A PAIR of TRIANGLES,
If one of the two similarity conditions is satisfied, the two triangles will be similar and the second similarity condition will automatically be true.
Simply speaking, if all three pairs of angles between corresponding sides are equal for two triangles, the triangles will be similar and the ratio of corresponding pairs of sides will also be equal, and vice versa.
This is only true for triangles.
In general,
For two polygons (except two triangles) to be similar to each other, all their corresponding angles must be equal, as well as ratio of their corresponding pair of sides must be equal.
This can be easily appreciated for a square and a rectangle. For both, all their internal angles are $90^0$ each, but by definition, all sides of a square are equal whereas only opposite parallel sides of a rectangle are equal, but adjacent sides are unequal. So ratio of corresponding pair of sides of a square and a rectangle are NOT EQUAL. That is why a square and a rectangle are dissimilar by their definition itself.
The following shows a square and a rectangle. They do not look alike. The rectangle is wider horizontally than it is high vertically, whereas, the square is as wide as it is high.
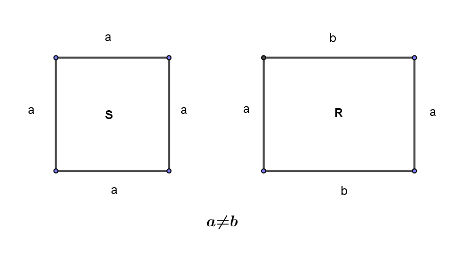
And the following shows a pair of dissimilar quadrangles with equal internal angles, but unequal ratios of corresponding sides.
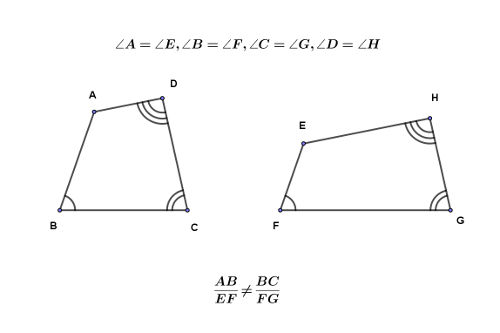
Even when the ratio of all pairs of corresponding sides of two polygons are equal, for similarity, their corresponding angles must be equal. In other words, two polygons (except triangles) to be similar, both the similarity conditions must be met.
This can easily be appreciated in the following case of a square with 3 unit side length and a rhombus with 4 units side length.
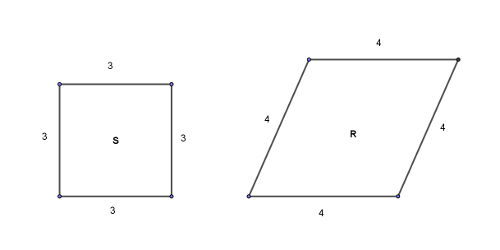
Ratios of all pairs of sides of the two are equal, but none of the pairs of angles are equal (you can't even fix corresponding pair of sides or angles). No doubt that these two are dissimilar.
Conditions for a pair of polygons to be congruent
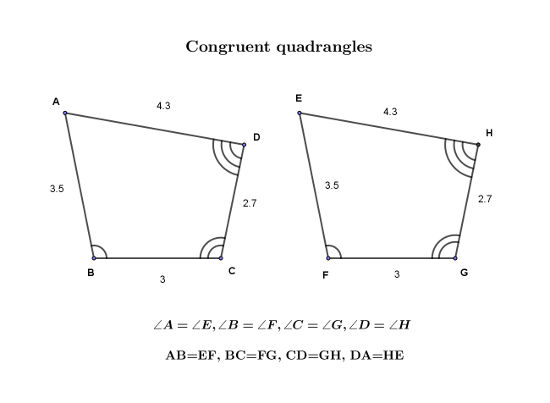
Two polygons are called as Congruent if they not only are similar but also ratios of all corresponding pairs of sides of the two is unity.
In other words, the two polygons are exact replica of each other. If one is superimposed on the other (vertices on corresponding vertices of course), the figure will look exactly like a single polygon.
The following figure shows two congruent quadrangles.
Solution to Exercise 6.1 NCERT Solutions class 10 maths on similarity of triangles and polygons
Questions
Q1. Fill in the blanks using the correct word given in the brackets:
- All circles are _______________. (congruent, similar)
- All squares are ________________. (similar, congruent)
- All ________________ triangles are similar (isosceles, equilateral)
- Two polygons of the same number of sides are similar, if (a) their corresponding angles are _____________ and (b) their corresponding sides are _________________. (equal, proportional)
Q2. Give two different examples of a pair of
i. similar figures ii. non-similar figures
Q3. State whether the following quadrilaterals are similar or not.

Answers to the questions
Q1. i. similar. Two circles would have been congruent only if their radii were equal, otherwise they are similar. This is a special property of circles.
Q1. ii. similar. Two squares would have been congruent exact replica of each other only if their side lengths were equal.
Q1. iii. equilateral. Two isosceles triangles not only may have unequal side ratios, but also unequal angles, but as all equilateral triangles have all their angles equal to $60^0$, they are similar.
Q1. iv. equal, proportional. Two polygons with same number of sides would be similar only if their corresponding angles were equal and corresponding sides were proportional with equal ratios.
Q2.i. Two circles are similar. Two squares are similar.
Q2.ii. A square and a rectangle are dissimilar by definition. An isosceles triangle and an equilateral triangle are dissimilar by definition.
Q3. No. ABCD being a square of all internal angles $90^0$ and PQRS being a rhombus with none of the internal angles $90^0$, the given quadrilaterals are not similar even though their side lengths are proportional.
NCERT Solutions for Class 10 Maths
Chapter 1: Real Numbers
NCERT Solutions for Class 10 Maths on Real numbers part 1, Euclid’s division lemma puzzle solutions
Chapter 2: Polynomials
Chapter 3: Linear Equations
NCERT solutions for class 10 maths Chapter 3 Linear equations 7 Problem Collection
NCERT solutions for class 10 maths Chapter 3 Linear equations 6 Reducing non-linear to linear form
NCERT solutions for class 10 maths Chapter 3 Linear Equations 4 Algebraic solution by Elimination
NCERT solutions for class 10 maths Chapter 3 Linear Equations 3 Algebraic solution by Substitution
NCERT solutions for class 10 maths Chapter 3 Linear Equations 2 Graphical solutions
NCERT solutions for class 10 maths Chapter 3 Linear Equations 1 Graphical representation.
Chapter 4: Quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 1 What are quadratic equations
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 2 Solving by factorization
NCERT solutions for class 10 maths Chapter 4 Quadratic Equations 3 Solution by Completing the square
Chapter 6: Triangles
NCERT solutions for class 10 maths chapter 6 Triangles 1 Similarity of Triangles and Polygons
Solutions to Exercise 2 Chapter 6 NCERT X Maths, Characteristics of Similar triangles
Chapter 8: Introduction to Trigonometry, Concepts and solutions to exercise problems
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 1 Trigonometric Ratios
NCERT solutions for class 10 maths chapter 8 Introduction to Trigonometry 4 Trigonometric identities
Chapter 8: Introduction to Trigonometry, only solutions to selected problems
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 6
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 5
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 4
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 3
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 2
NCERT Solutions for Class 10 Maths on Trigonometry, solution set 1