1st IBPS PO level Solution Set, 1st on topics Speed-time-distance, Train running and Boats in rivers

This is the 1st solution set of 10 practice problem exercise for IBPS PO exam and 1st on topic Speed-time-distance, Train running and Boats in rivers. Students must complete the corresponding question set in prescribed time first and then only refer to this solution set for gaining maximum benefits from this resource.
In MCQ test, you need to deduce the answer in shortest possible time and select the right choice.
Based on our analysis and experience we have seen that, for accurate and quick answering, the student
- must have complete understanding of the basic concepts in the topic area
- is adequately fast in mental math calculation
- should try to solve each problem using the basic and rich concepts in the specific topic area and
- does most of the deductive reasoning and calculation in his or her head rather than on paper.
Actual problem solving is done in the fourth layer. You need to use your problem solving abilities to gain an edge in competition.
If you have not taken the test yet, before going through the solutions you should do it by referreing to,
IBPS PO level Question set 1 on speed time distance, train running, boats in rivers 1.
1st solution set - 10 problems for IBPS PO exam: 1st on topics Speed-time-distance, Train running, Boats in rivers - time 12 mins
Problem 1.
Two trains moving in the same direction pass each other in 3 mins 2 secs while moving in opposite directions pass each other in 14 secs. How much more in percentage is the speed of the faster train in comparison to the slower one?
- 16.33%
- 17.67%
- 16.67%
- 18.33%
- 17.33%
Solution 1: Problem analysis and solution
The basic train passing concept is,
To pass each other, two trains have to travel their total length at their relative speed.
This is true whether their direction of movements are opposite to each other or same.
If they move in same direction, their relative speed is,
$V_1-V_2$, where $V_1$ and $V_2$ are the speeds of the faster and the slower trains.
At this relative speed, the distance of total length $L$, say, would be covered in time,
$\displaystyle\frac{L}{V_1-V_2}=182\text{ secs}$, 3 minutes 2 secs is converted to secs,
Similarly the time to pass each other moving in the opposite direction at relative speed of $(V_1+V_2)$ will be,
$\displaystyle\frac{L}{V_1+V_2}=14\text{ secs}$
Dividing the first equation by the second we get,
$\displaystyle\frac{V_1+V_2}{V_1-V_2}=13$
Applying three-step componendo dividendo on the last equation (add 1 to both sides, subtract 1 from both sides, take the ratio of the two results), we get,
$\displaystyle\frac{V_1}{V_2}=\displaystyle\frac{14}{12}$,
Or, $\displaystyle\frac{V_1-V_2}{V_2}=\displaystyle\frac{1}{6}=16.67$%.
This is the desired percentage of the slower train speed by which the faster train exceeds the speed of the slower train.
Answer. Option c: 16.67%.
Key concepts used: Basic speed time distance concepts -- Train passing concept -- Train running -- Relative speed concept -- Componendo dividendo -- Percentage reference concept -- Efficient simplification -- Solving in mind.
Note: Application of three-step Componendo dividendo method made solving in mind easier, but one must note the percentage reference as the slower train speed without which the answer will come incorrect.
Problem 2.
A man travels from A to B at speed 40 km/hr and returns to A by increasing his speed to 150%. What is his average speed for both the trips combined?
- 36 km/hr
- 50 km/hr
- 45 km/hr
- 48 km/hr
- None of the above
Solution 2: Problem analysis and solution
Forward and return speeds were 40 km/hr and 60 km/hr with distance remaining same. So average speed is related by the times taken to cover the two distances,
$\displaystyle\frac{d}{40}+\displaystyle\frac{d}{60}=\displaystyle\frac{2d}{V}$, where $V$ km/hr is assumed to be the average speed over two trips
Or, $\displaystyle\frac{5}{120}=\frac{2}{V}$, one trip distance $d$ cancels out
Or, $V=48$ km/hr.
By the total time the man completed his forward trip and return trip each of distance $d$ km, effectively he covered a distance of $2d$ km at average speed of $V$ km/hr.
Answer: Option d: 48 km/hr.
Key concepts used: Speed time inverse proportionality with distance constant -- Average speed -- Solving in mind.
Problem 3.
A train traveling at 51 km/hr passes in 24 seconds a second train double its length moving in opposite direction at a speed of 93 km/hr. If the second train also passes a bridge in 66 seconds, the length of the bridge is,
- 1705 m
- 1600 m
- 1580 m
- 1065 m
- None of the above
Solution 3: Problem analysis and solution
Let $L$ m be the length of the first train and $B$ m be the length of the bridge. By problem statement then length of the second train is $2L$ m.
When the two trains pass each other in opposite directions they have to cover their total length $3L$ m at the relative speed of $(51+93)=144$ km/hr, and so the time they take would be,
$\displaystyle\frac{3L\times{3.6}}{144}\text{ sec}=24\text{ sec}$, we have converted km/hr in the denominator to m/sec by dividing 1000 m by 3600 sec
So,
$L=\displaystyle\frac{144}{3.6}\times{8}=320$ m.
In the second case when the second train passes the bridge it covers a length of $(2L+B)$ m length at a speed of 93 km/hr. So by speed time distance relation of,
$\text{Time}=\displaystyle\frac{\text{distance}}{\text{speed}}$, we have here,
$\displaystyle\frac{(640+B)\times{3.6}}{93}\text{ secs}=66\text{ secs}$
Or, $640+B=\displaystyle\frac{93\times{66}}{3.6}=55\times{31}=1705$
So length of bridge,
$B=1705-640=1065$ m.
Answer: Option d: 1065 m.
Key concepts used: Train passing concepts -- Train running -- Relative speed concept -- Speed time distance relation -- Platform or bridge passing concept.
To ensure accuracy of the calculations in two cases, we needed to write the speed time distance relations in the two cases. Solving was quick and easy enough sticking to the basic concepts.
Problem 4.
To travel a certain distance $D$ km in a river downstream, a boat takes the same time it takes to travel $(D-12)$ km upstream. If the ratio of speed of the river current and the speed of the boat in still water is $1:5$, find the value of $D$.
- 36 km
- 28 km
- 30 km
- 24 km
- 32 km
Solution 4: Problem analysis and solution
When a boat travels in a river downstream, effective speed of the boat with respect to a man standing still on the bank of the river becomes its still water speed $V$ plus the river current speed $S$, that is,
$(V+S)$.
Upstream though, the river current opposes the progress of the boat and its effective speed becomes,
$(V-S)$.
In the problem, ratio of the speeds given is,
$S : V=1:5$
Or $V=5S$.
So from first two given conditions we would get the relation between the times taken upstream and downstream travels as,
$\displaystyle\frac{(D-12)}{V-S}=\frac{D}{V+S}$,
Or, $\displaystyle\frac{D-12}{4S}=\frac{D}{6S}$,
Or, $3D-36=2D$, $S$ cancels out,
Or, $D=36$ km.
Answer: Option a: 36 km.
Key concepts used: Boats in rivers concepts -- upstream speed concept -- downstream speed concept -- Speed time distance relation -- Solving in mind.
Problem 5.
In covering 28 km downstream, a boat takes 35 mins less than it takes to cover the same distance upstream. If the speed of the boat in still water is 14 km/hr, what is the speed of the stream (in km/hr)?
- 2.5
- 10.5
- 2
- 9.5
- 6.5
Solution 5: Problem analysis and solution
Upstream time,
$T=\displaystyle\frac{28}{14-S}$, where $S$ is stream speed.
Similarly downstream time,
$T-\displaystyle\frac{7}{12}=\displaystyle\frac{28}{14+S}$, 35 mins is converted to hours for unit matching; fraction form is easier to evaluate
Subtracting second from first,
$\displaystyle\frac{7}{12}=28\left(\displaystyle\frac{1}{14-S}-\displaystyle\frac{1}{14+S}\right)$,
Or, $\displaystyle\frac{1}{48}=\displaystyle\frac{2S}{14^2-S^2}$,
Or, $14^2-S^2=96S$
Or, $S^2+96S-196=0$,
Or, $(S-2)(S+98)=0$.
So, $S=2$ km/hr as it can't be negative.
Answer: Option c: 2 km/hr.
Key concepts used: Boats in rivers concepts -- Speed time distance relation -- Solving quadratic equation by mid-term splitting.
Problem 6.
A train starts from station P at 8 am and travels at speed 53 km/hr towards station Q from where a second train starts at 9 am and travels at speed 76 km/hr towards station P. If distance between the two stations were 569 km, at what time will the trains meet?
- 2 pm
- 12.30 pm
- 1.30 pm
- 2.30 pm
- 1 pm
Solution 6: Problem analysis and solution
When two trains starting at the same time from two stations travel towards each other,
- the two trains together cover the distance between the two stations when they meet,
- relative speed at which the trains cover the distance is the sum of their individual speeds, and
- the two trains run for the same time to meet.
The following figure depicts an example case of two trains traveling at speeds 20 km/hr and 60 km/hr starting at the same time from two stations distant 160 km towards each other and meeting after 2 hrs. They cover the total distance of 160 km at relative speed of $(20+60)=80$ km/hr.

In this problem then the first train starts 1 hour earlier at 53 km/hr to cover 53 km when the second train starts. So the two trains now would cover the remaining distance $(569-53)=516$ km moving at relative speed $(53+76)=129$ km/hr. The time taken to cover this distance would then be,
$\displaystyle\frac{516}{129}=4$ hrs.
Counting 4 hrs from 9 am, the clock time when the two trains meet would be,
$9\text{ am }+ 4\text{ hrs }=1\text {pm}$.
9 am is the later time when both the trains simultaneously start running towards each other.
Answer: Option e: 1 pm.
Key concepts used: Relative speed -- Trains from two stations moving towards each other to meetContext awareness -- Solving in mind.
Example of context awareness here is the awareness of the fact that the second train had started 1 hour after the first train and in this 1 hour the first train already covered 53 kms. So the trains moving towards each other to meet concepts are to be applied on the distance of 516 km remaining, and not on the original distance of 569 kms.
Problem 7.
A truck covers 528 km in a certain time moving at an average speed of 66 km/hr. If a car moving at an average speed less by 24 km/hr than the truck travels 7 hrs more than the time taken by the truck, how much distance will it cover?
- 336 km
- 630 km
- 598 km
- 682 km
- None of the above
Solution 7: Problem analysis and solution
By first statement, the truck covers 528 km in a time of,
$\displaystyle\frac{528}{66}=\frac{88}{11}=8$ hrs
So the car moving at an average speed of, $(66-24)=42$ km/hr will travel in a time of, $(8+7)=15$ hrs, a distance of,
$42\times{15}=630$ km
Answer: Option b: 630 km.
Key concepts used: Speed time distance relation -- Solving in mind.
Problem 8.
Among three points on the bank of a river flowing at a constant current speed, Q is at equal distances from P and R. A man swims for 10 hrs to reach Q from P and then back to P. Further, he takes 4 hrs to swim from P to R. What is the ratio of the swimming speed of the man in still water and the speed of the river current?
- 3 : 5
- 5 : 3
- 1 : 2
- 2 : 5
- 3 : 2
Solution 8: Problem analysis
First observation on location of Q:
As Q is at equal distances from P and R, it is situated at the middle point of P and R.
Second observation on river current direction with respect to P, Q and R sequence:
From the statement of time taken to swim from P to Q and back to P is 10 hrs, no conclusion regarding the river current direction can be made. But from the statement that time to swim all the way from P to R crossing Q midway is only 4 hrs, it can be concluded that the swimmer swims downstream from P to R. Otherwise it would have been more than 10 hrs.
These are the key patterns identified to precisely define the problem.
Solution 8: Problem solving
Let us assume the still water swimming speed as $V$ km/hr, river current speed as $S$ km/hr and distance between P to Q and Q to R as $d$ km
For the swim from P to Q and back to Q in 10 hrs we have then,
$10=\displaystyle\frac{d}{V+S}+\displaystyle\frac{d}{V-S}$.
And for the swim from P to R in 4 hrs we have,
$4=\displaystyle\frac{2d}{V+S}$,
Or, $\displaystyle\frac{d}{V+S}=2$.
Substituting in first equation,
$10=2+\displaystyle\frac{d}{V-S}$,
Or, $\displaystyle\frac{d}{V-S}=8$.
Taking the ratio of the two results,
$\displaystyle\frac{V+S}{V-S}=4$.
Applying three-step componendo dividendo (adding 1, subtracting 1 and taking ratio of the results),
$\displaystyle\frac{V}{S}=\frac{5}{3}$.
Answer: Option b: 5 : 3.
Key concepts used: Problem analysis -- Problem modelling -- Key pattern identification -- Boats in rivers concepts -- Speed time distance relation -- Componendo dividendo -- Solving in mind.
Once the problem is precisely defined it could be quickly solved in mind. Mark that the problem is solved using the very basic concepts only, though use of componendo dividendo helped to speed up the solution.
Problem 9.
Two boats P and Q with still water speeds 12 km/hr and 15 km/hr respectively, start at the same time towards each other from two points 108 km apart. If P moves downstream and Q upstream, they will meet after a time period of,
- 4.5 hrs
- 6 hrs
- 4 hrs
- 5.4 hrs
- 6.3 hrs
Solution 9: Problem analysis and solution
Assuming that the stream speed is $S$ km/hr, the effective speed of P will be, $(12+S)$ km/hr and that of Q, $(15-S)$ km/hr and their relative speed,
$12+15=27$ km/hr.
To meet, the two will cover the distance of 108 km, at the relative speed of 27 km/hr in,
$\displaystyle\frac{108}{27}=4$ hrs.
Answer: Option c: 4 hrs.
Key concepts used: Basic speed, time and distance concepts -- Problem analysis -- Problem modelling -- Boats in rivers concepts -- Concepts of Two objects moving towards each other and meet -- Solving in mind.
It was easy to see that when we evaluate the relative speed by summing up the effective speeds of the two, the stream speed will cancel out. Solution would be just a simple step away. This problem depends on clear understanding of the concepts involved.
Problem 10.
Two cars A and B left point P moving in the same direction at 9 am and 9.30 am with constant speeds 45 km/hr and $V$ km/hr respectively. If car B traveled 90 km before it met car A what is the value of $V$?
- 120 km/h
- 90 km/h
- 60 km/hr
- 40 km/hr
- 75 km/h
Solution 10: Problem analysis and solution
It is a problem of race under handicap with faster car B starting late giving a handicap of 30 minutes to the slower car A before catching it up after traveling for 90 km. In this period of 30 minutes car A covered 22.5 km. This is the handicap to car B. Car A was 22.5 km ahead when car B started at 9.30 am.
The following figure represents the situation.
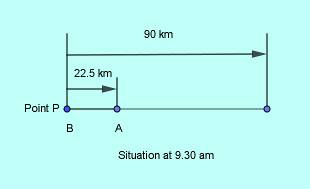
As car B traveled 90 km to catch up car A the distance car A traveled by that time was $90-22.5=67.5$ km and it took $\displaystyle\frac{67.5}{45}=1.5$ hr to cover that up to the meeting point.
Car B covered 90 km also in 1.5 hr and so its speed was, $\displaystyle\frac{90}{1.5}=60$ km/hr.
Answer. Option c: 60 km/hr.
Key concepts used: Basic speed time distance relation -- Race concepts -- Handicap -- Visualization -- Solving in mind.
If you can visualize what really happened, where which car was at what time, the problem is simple enough to be solved quickly in mind.
Note: Though the problem refers to a race, for solving the problem use of race concept and techniques of relative speed are not involved.
Resources for further reading on related topics
The following posts on related topics should be useful for you.
Tutorials and Quick solutions in a few steps on Speed time distance and related topics
Basic concepts on Arithmetic problems on Speed-time-distance Train-running Boat-rivers
How to solve Time and Distance problems in a few simple steps 1
How to solve Time and Distance problems in a few simple steps 2
How to solve a GATE level long Work Time problem analytically in a few steps 1
How to solve arithmetic boundary condition problems in a few simple steps
How to solve Arithmetic problems on Work-time, Work-wages and Pipes-cisterns
IBPS level Question and Solution sets on speed time distance, train running, boats in rivers
IBPS PO level Solution set 1 on speed time distance, train running, boats in rivers 1
IBPS PO level Question set 1 on speed time distance, train running, boats in rivers 1