
Geometry solutions for SSC CGL Tier 2 Set 15
Learn how to solve the 10 selected questions on geometry for SSC CGL Tier 2 set 15 in 15 minutes' time by geometry problem solving concepts and techniques.
The 10 SSC CGL Tier II level questions are on, median ratio at centroid, properties of a rhombus, properties of diagonals of a parallelogram, equilateral triangle, angle subtended by an arc of a circle, cyclic quadrilateral, similar triangles, isosceles triangle, right angled triangle and much more.
These are comparatively difficult geometry questions to solve.
If you have not yet taken this test take it first at,
SSC CGL Tier II level question set 15 on Geometry 4.
How to solve Geometry for SSC CGL Questions Tier 2 Set 15 - answering time was 15 mins
Problem 1.
If G is the centroid of an equilateral triangle ABC with side length 10 cm, then the length of AG is,
- $5\sqrt{3}$ cm
- $10\sqrt{3}$ cm
- $\displaystyle\frac{5\sqrt{3}}{3}$ cm
- $\displaystyle\frac{10\sqrt{3}}{3}$ cm
Solution 1: Problem analysis and solving execution
The following figure describes the problem solution,
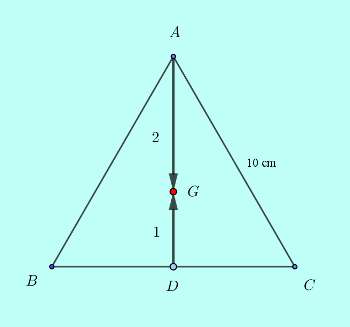
Even without the figure: if we draw a median AD from vertex A, it is divided at centroid in length ratio $2:1$, the larger part towards A and the smaller one towards side BC opposite to A. This is true for any triangle.
So, if G is the centroid, it divides the median AD in a ratio $2:1$, that is, $AG:GD=2:1$. It follows, the ratio, $AG:AD=2:3$.
Additionally, for an equilateral triangle the median plays the double role of perpendicular bisector of the opposite side. In this case, AD is perpendicular bisector of BC. So, even without the figure we can evaluate the length of AD in a right triangle $\triangle ACD$ as,
$\text{AD}^2=10^2-5^2=75$, by Pythagoras theorem
Or, $\text{AD}=5\sqrt{3}$ cm.
So, the larger part of AD, that is,
$\text{AG}=\displaystyle\frac{2}{3}\times{5\sqrt{3}}=\displaystyle\frac{10\sqrt{3}}{3}$ cm.
Answer: Option d: $\displaystyle\frac{10\sqrt{3}}{3}$ cm.
Key concepts used: Median section ratio at centroid -- Median as perpendicular bisector of opposite side in an equilateral triangle -- Pythagoras theorem.
Problem 2.
If the ratio of the angles of a quadrilateral is $2:7:2:7$, then the shape
- is a rhombus
- is a parallelogram
- is a trapezium
- cannot be identified
Solution 2: Problem analysis and solving
By HCF reintroduction technique in a ratio, if $x$ is the cancelled out HCF in the given ratio, the total of the angles is,
$2x+7x+2x+7x=18x=360^0$,
Or, $x=20^0$.
Two opposite angles each is then $40^0$, and the other two each is $140^0$. The quadrilateral must then be either a parallelogram or a rhombus.
In a rhombus, the diagonals bisect the respective corner angles as well as the adjacent sides are of equal length. Either of these two properties differentiates a rhombus from a parallelogram at a more granular level.
This is a rich concept. Unless you are aware of this concept, correctness of your answer would be uncertain.
In our problem, none of these two properties to differentiate between a rhombus and a parallelogram can be identified. In short, sufficient information is not available to differentiate between the two possible options b and c.
So the answer would be Option d.
The following are a rhombus and a parallelogram both with angles, $40^0$, $140^0$, $40^0$ and again $140^0$.

We just have glided the side CD along the dotted parallel guides away from AB but keeping it parallel to AB to transform the Rhombus to a parallelogram without changing value of any of the angles. Possibly now you can realize visually why only the value of angles cannot differentiate between two possibilities. This is what we call Visualization. Instead of actually drawing the rhombus and taking the action of sliding, you can visualize the concept to understand why it is not possible to differentiate between the possibility of a parallelogram and a rhombus with the given information.
Caution: Whenever you encounter rhombus and parallelogram as two possible choices, be extra cautious in making your decision.
In the section below, we have briefly stated the properties and explained the reason behind the properties of a trapezium, parallelogram, rhombus and a square.
Properties of special types of quadrilaterals on a plane
A general quadrilateral is a shape bounded by four sides. It has no specialties of side lengths, positional relations between sides or the four angles. All four side lengths and angles are unequal respectively, as well as no two sides are parallel to each other.
Properties of a Trapezium
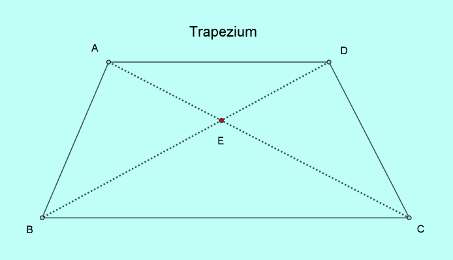
In a trapezium first element of specialty or symmetry is observed in the form of two parallel sides. With a little bit more symmetry, angles adjacent to each parallel side may be equal to each other. In figure below, $\angle BAD$ may be equal to $\angle CDA$ as well as $\angle ABC=\angle BCD$, but more importantly, one pair of sides in a trapezium $AD || BC$. This is the only symmetry expected in a trapezium.
Question: Is it possible to have more symmetry in a trapezium?
Properties of a Parallelogram
At the next stage of increasing symmetry, in a parallelogram, two pairs of sides are parallel as well as equal in length. The property of two pairs of sides parallel automatically results in the pairs of sides equal in length as well as opposite pairs of angles equal. Additionally, the diagonals bisect each other at their intersection point E.
Reason of equality of opposite pair of angles: As $AD || BC$, $\angle DBC=\angle BDA$. Also, because $AB || DC$, $\angle ABD=\angle BDC$. So their sum, the opposite pair of angles, $\angle ABC=\angle ADC$. Similarly, $\angle BAD=\angle BCD$.
Reason of diagonals bisecting each other at their intersection point E: As all three corresponding angles are equal, $\triangle AED$ and $\triangle BEC$ are similar with equal ratio of corresponding sides. In these two similar triangles, as sides $AD=BC$ other two pairs must then be equal, $AE=CE$ and $BE=DE$.

Properties of a Rhombus
At the third stage of increasing symmetry, in a rhombus which is a special type of parallelogram, all four sides are equal, two pairs of sides parallel to each other, opposite pairs of angles equal, and additionally, the two diagonals bisect themselves and also bisect respective corner angles. Furthermore, the diagonals are perpendicular to each other.
Reason of diagonals of a rhombus bisecting respective corner angles: As $AB=AD$, $\angle ABD=\angle ADB$. Also, with $AB||DC$, $\angle ABD=\angle BDC$. So, $\angle ADB=\angle BDC$, that is, diagonal BD bisects $\angle ADC$. Similarly it also bisecs $\angle ABC$, and the other diagonal AC bisects its respective two corner angles.
Reason for diagonals in a rhombus perpendicular to each other: In $\triangle ABC$, BE bisects base AC, that is BE is a median. But as $AB=BC$ in the isosceles triangle, the median bisects the base AC perpendicularly.

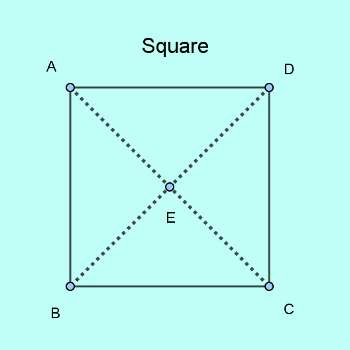
Properties of a Square
At the fourth stage of increasing symmetry, in a square which is a special type of rhombus, all four angles are equal and $90^0$. In a square, all four sides and angles are equal. The angles are all $90^0$. Two pairs of sides are parallel to each other and the diagonals are of equal length, corner angle bisectors and perpendicular bisectors to each other.
Answer: Option d: cannot be identified.
Key concepts used: HCF reintroduction technique -- Ratio concepts -- Angles in quadrilaterals -- Increasing symmetry in quadrilaterals -- Properties trapezium, parallelogram, rhombus and square -- Visualization -- Differentiating between two close by possibilities -- Shape transformation.
Visualization
Simply speaking, visualization is imagination to create a scenario in mind. We use visualization in more specific ways, using different mechanisms in different problem areas and problems to transform a scenario to another close by scenario. In this problem we have used visualization to transform a rhombus to a close by nearly similar shape of parallelogram. To visualize we have used sliding or translation of one side of the rhombus in a controlled manner, imagining the process in mind. Result has been clarity and answer. In a different geometry problem we may need to use different mechanism of transformation to visualize.
In general, visualization in problem solving to be effective, the important aspects we observe are,
- Visualization would involve two scenarios both of which are nearly similar possibilities towards solution. In geometry it would be shape configurations.
- In effective visualization, the two possibilities should be as similar or close by as possible. In business, the starting point may be analyzed and processed business state and the second the desired business state. In geometry the starting shape may again be a shape configuration arrived at after initial analysis and the second, a similar possible shape towards solution.
- There would always be transformation from one state to the other. The transformation process will bring to light clearly the aspects that differentiate the two possibilities.
- The transformation mechanism would differ from problem to problem, domain to domain, but it should be as simple as possible to be really effective. Simpler is the transformation mechanism, faster is the transformation and resulting solution. Though it may seem there are large number of mechanisms possible in a domain, but it is not so; commonality and classification of transformation mechanism can be achieved by using abstraction and generalization. For example, in geometry, three possible mechanisms that we may have to use with more frequency are, controlled translation of a part of the shape being transformed, controlled rotation of a part of the shape being transformed, or simply introduction of one or two new elements at the right place in the shape being transformed. We have used the first mechanism to transform a rhombus to a parallelogram and thereby achieved clear distinction between the two shapes pertinent to the problem. We will use the third mechanism in a later problem to solve it in mind in a few tens of seconds.
Problem 3.
If $D$, $E$ and $F$ are the mid-points of sides $BC$, $CA$ and $AB$ respectively of $\triangle ABC$, then the ratio of the area of the parallelogram $DEFB$ and the area of the trapezium $CAFD$ is,
- $2:3$
- $3:4$
- $1:3$
- $1:2$
Solution 3: Problem analysis and solving
To visualize easily let us quickly draw the simple shape as below,

The three dotted lines divide the triangle into four parts. Now we need to visualize CDFE as a parallelogram with DE as its diagonal. As a line joining mid-points of two sides is parallel to the third side in a triangle, by problem definition, CDFE is a parallelogram.
Using the concept that a diagonal of a parallelogram divides a parallelogram into two equal parts, it follows that areas of triangles, $\triangle DFE$ and $\triangle DCE$ are equal. Similarly area of the triangles, $\triangle DFE$ is equal to that of $\triangle FAE$ and also $\triangle DBF$. Essentially four areas marked as $a$ are all equal.
Coming to the last stage, we count 2 triangles marked as "a" and of equal area making up parallelogram $DEFB$ and 3 triangles marked as "a" and of equal area making up trapezium $CAFD$.
So the desired ratio is $2:3$.
Answer: Option a: $2:3$.
Key concepts used: Triangle rich concepts -- Parallelogram diagonal properties -- Deductive reasoning -- Area as a component -- Ratio concepts.
Problem 4.
If a chord of a circle is equal to its radius, the angle subtended by the chord at the minor arc of the circle is,
- $60^0$
- $150^0$
- $120^0$
- $75^0$
Solution 4: Problem analysis and solving
The following figure depicts the given problem.

As given, the length of chord AB and radius AO are equal. In $\triangle AOB$ then all three sides are equal. It is an equilateral triangle, its angles each is $60^0$. So the external $\angle AOB$ held by the major arc on chord AB is, $360^0-60^0=300^0$.
By arc angle subtending concept, the angle held by the chord AB on any point P of the complementary arc, which is the minor arc here, is half of $300^0$, that is $150^0$.
To refresh the concept you may refer to the fourth configuration in our comprehensive article on the topic,
Basic and rich Geometry concepts 4, proof of Arc angle subtending concept.
This is the fastest way to the solution and achieved mentally.
Answer: Option b: $150^0$.
Key concepts used: Identifying the key pattern of equilateral triangle -- Angle properties of an equilateral triangle -- Angle subtending concept on minor arc.
Note: It is the use of a rich concept and that is why solution is so quick and easy.
Problem 5.
In a cyclic quadrilateral ABCD, AB and DC when extended meet at point P. If PA= 8 cm, PB = 6 cm and PC = 4 cm, the length of PD in cm is,
- 10 cm
- 12 cm
- 6 cm
- 8 cm
Solution 5: Problem analysis and solving
The figure depicting the problem is shown below.
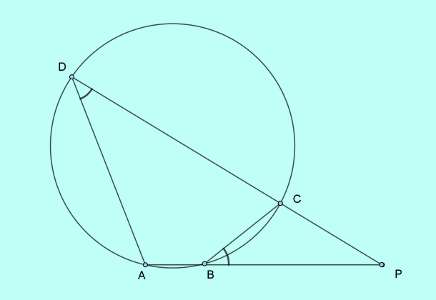
As only length of three sides are given with the length of the fourth side wanted, it is a clear case of finding two similar triangles in which ratio of two pairs of corresponding sides will be equal.
The key pattern is straightforward, $\angle P$ is common to $\triangle DAP$ and $\triangle BCP$, as well as, $\angle CBP= \angle ADP$, as in the cyclic quadrilateral with opposite pair of angles sum up to $180^0$,
$\angle ADP+\angle ABC=180^0=\angle ABC+\angle CBP$.
With two angles equal, the third angle must be equal and the two triangles, $\triangle ADP$ and $\triangle BCP$ are similar.
We select two convenient pair of corresponding sides in these two similar triangles, and equalize their ratios. In the two ratios there should be three known lengths and a fourth unknown length of side PD,
$\displaystyle\frac{PD}{PB}=\frac{PA}{PC}$,
Or, $PD=6\times{\displaystyle\frac{8}{4}}=12$ cm
Answer: Option b: 12 cm.
Key concepts used: Deductive reasoning with expectation of two similar triangles as the key to the solution -- Visualization to find the key common $\angle P$ identifying two candidate triangles -- Angles at point of incidence property and Cyclic quadrilateral property together deliver the second pair of equal angles -- equal ratio of corresponding pair of sides in two similar triangles -- Similar triangles side ratio equality.
Problem 6.
In $\triangle ABC$, $DE||BC$ and $AD:DB=5:4$. Then the ratio, $DE:BC$ is,
- $4:5$
- $9:5$
- $5:9$
- $4:9$
Solution 6: Problem analysis
The following figure depicts the problem statement.
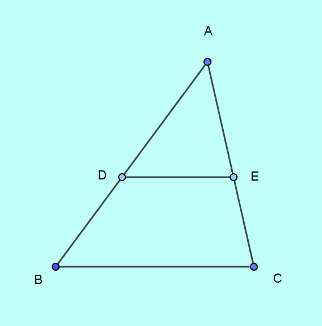
DE parallel to base BC creates two similar triangles, $\triangle ABC$ and $\triangle ADE$.
Given,
$AD:DB=5:4$,
Or, $\displaystyle\frac{DB}{AD}=\frac{4}{5}$.
Adding 1 to both sides,
$\displaystyle\frac{DB+AD}{AD}=\frac{9}{5}$,
Or, $\displaystyle\frac{AB}{AD}=\frac{BC}{DE}=\frac{9}{5}$.
So the inverse ratio, $DE:BC=5:9$.
Answer: Option c: $5:9$.
Key concepts used: A line parallel to the base of triangle creating two similar triangles -- Ratio concepts -- Ratio of Corresponding sides of two similar triangles are equal.
Problem 7.
In a $\triangle ABC$, $BC=12$ cm. A line CD is drawn to intersect AB at D internally. If $DB=9$ cm, $CD=6$ cm and $\angle BCD=\angle BAC$, ratio of the perimeter of $\triangle ADC$ to that of $\triangle BDC$ is,
- $\displaystyle\frac{5}{9}$
- $\displaystyle\frac{6}{9}$
- $\displaystyle\frac{7}{9}$
- $\displaystyle\frac{8}{9}$
Solution 7: Problem analysis, key pattern identification, strategy decision and solution
The following figure depicts the problem situation.
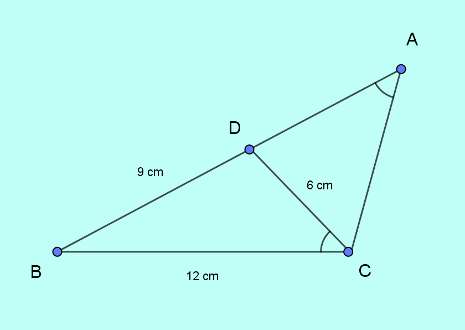
The key pattern in the problem is,
length of three sides are given; one pair of angles are equal and there seems to be no possibility of working on right triangles with any one angle $90^0$.
The problem statement clearly creates a pair of triangles and the desired result is in terms of length of sides.
By deductive reasoning we decide that the way to finding two similar triangles with equal side length ratios as the most prospective one under the circumstances. Especially, the angle equality should point out which two triangles we should pair up for similarity. This is our strategy decision of using the similar triangle pattern identification technique.
As expected, $\triangle BCD$ and larger triangle, $\triangle ABC$ are identified to be similar easily. One angle equality is already given, the second angle $\angle B$ is common to both triangles. So the third angle pair must also be equal. This pattern identification technique often gives us two not so easily visible similar triangles.
Using the given lengths of sides, we can form suitable equal ratios of corresponding sides in the two triangles $\triangle ABC$ and $\triangle BCD$, and determine the length of the sides that are unknown. This is the method applicable here.
Using the property of equal ratio of lengths of corresponding sides in two similar triangles, first we derive the length of AC,
$\displaystyle\frac{AC}{CD}=\frac{BC}{BD}$,
Or, $AC=6\times{\displaystyle\frac{12}{9}}=8$ cm.
And then we derive the length of the third side AB of $\triangle ABC$,
$\displaystyle\frac{AB}{BC}=\frac{BC}{BD}=\frac{12}{9}$,
Or, $AB=\displaystyle\frac{144}{9}=16$ cm.
The length of the third side AD of target triangle $\triangle ADC$ is,
$AB-BD=16-9=7$ cm.
So the desired ratio of perimeters of two triangles $\triangle ADC$ and $\triangle BDC$ is,
$\displaystyle\frac{7+6+8}{9+12+6}=\frac{21}{27}=\frac{7}{9}$.
Answer: Option c: $\displaystyle\frac{7}{9}$.
Key concepts used: Deductive reasoning to identify similarity of two triangles to be the key pattern we have to find -- two equal angles and a common angle quickly identify two similar triangles -- Pattern identification technique -- equal ratios of corresponding sides give us the required lengths of sides in stages -- Similar triangle side ratio equality.
Going similar triangle way has been crucial in solving the problem in a few steps.
Problem 8.
In the figure below, chord $CD$ is parallel to diameter $AB$ of a circle with centre at $O$.

If $\angle CEB=65^0$, then $\angle BCD$ is,
- $25^0$
- $35^0$
- $55^0$
- $45^0$
Solution 8: Problem analysis and solving
The following figure will aid solution of the problem.

We introduce a new geometric element, that is, line OC, as a key to the solution. This is the second use of visualization. The two radii OC and OB form an angle held by the chord BC at the centre O.
By arc angle subtending concept, this angle $\angle COB$ is double the angle held by the chord BC at any point E on the major arc which is $65^0$.
With $\angle COB=130^0$ in the isosceles triangle $\triangle COB$, other two angles are equal and sums up to, $180^0-130^0=50^0$.
So,
$\angle BCD=\angle CBO=25^0$, as $CD||AB$.
Answer: Option a: $25^0$.
Answer comes quickly just by visualization of the pattern that was not present in the given figure and use of basic and rich concepts of arc angle subtending concept, isosceles triangle property and parallel lines property.
Key concepts used: Geometric element introduction technique -- Visualization -- arc angle subtending concept -- Property of isosceles triangle -- properties of a line intersecting two parallel lines.
Problem 9.
In $\triangle ABC$, the line $BB_1$ through $B$ intersects side $AC$ at $B_1$. A line through $A$ parallel to $BB_1$ meets $CB$ extended at $A_1$ and another line through $C$ parallel to $BB_1$ meets $AB$ extended at $C_1$. Then which of the following is true?
- $\displaystyle\frac{1}{AA_1}-\displaystyle\frac{1}{CC_1}=\displaystyle\frac{2}{BB_1}$
- $\displaystyle\frac{1}{BB_1}-\displaystyle\frac{1}{AA_1}=\displaystyle\frac{2}{CC_1}$
- $\displaystyle\frac{1}{CC_1}+\displaystyle\frac{1}{AA_1}=\displaystyle\frac{1}{BB_1}$
- $\displaystyle\frac{1}{CC_1}-\displaystyle\frac{1}{AA_1}=\displaystyle\frac{1}{BB_1}$
Solution 9: Problem analysis, pattern identification and strategy decision
The following figure represents the problem definition.

The key pattern we identify as the two sets of similar triangles, $\triangle ACA_1$, $\triangle B_1CB$ and $\triangle CC_1A$, $\triangle B_1BA$. The reason behind the pairs of triangles to be similar being, $AA_1||B_1B$ and $CC_1||B_1B$.
The two target ratios, $\displaystyle\frac{BB_1}{AA_1}$ and $\displaystyle\frac{BB_1}{CC_1}$ are easily visible, but these two are to be related together. The only way to do this we find, is to involve ratios on the side $AC$ common to the two sets of similar triangles.
We plan to use AC as the link element to relate the two target side ratios.
This must be the decision that would lead us to the solution quickly.
Solution 9: Problem solution using similar triangle property of corresponding side ratio equality and algebraic manipulation
By the similar triangle property of corresponding side ratio equality, in the similar pair of triangles $\triangle ACA_1$ and $\triangle B_1CB$,
$\displaystyle\frac{BB_1}{AA_1}=\frac{B_1C}{AC}$.
Similarly in the pair of similar triangles, $\triangle CC_1A$ and $\triangle B_1BA$,
$\displaystyle\frac{BB_1}{CC_1}=\frac{AB_1}{AC}$.
The two ratios are nearly but not fully equal. A small algebraic manipulation though makes the two equal.
By subtracting both sides of second equation from 1 we get,
$1-\displaystyle\frac{BB_1}{CC_1}=\frac{AC-AB_1}{AC}=\frac{B_1C}{AC}$.
So,
$\displaystyle\frac{BB_1}{AA_1}=1-\displaystyle\frac{BB_1}{CC_1}$,
Rearranging the terms and taking $BB_1$ to the RHS denominator,
$\displaystyle\frac{1}{CC_1}+\displaystyle\frac{1}{AA_1}=\displaystyle\frac{1}{BB_1}$.
Answer: Option c: $\displaystyle\frac{1}{CC_1}+\displaystyle\frac{1}{AA_1}=\displaystyle\frac{1}{BB_1}$.
Key concepts used: Visualization to draw the diagram -- Identifying the key pattern of two pairs of similar triangles with two of the target term ratios -- Strategy decision of relating the two ratios using the common side $AC$ -- Link element use technique -- Similar triangle corresponding side ratio equality -- Algebraic manipulation to equalize the two target ratios -- Algebraic simplification.
The problem though looked awkward could finaly be solved reasonably quickly by identifying the key pattern and relating the two target ratios using the ratios on the common side. A rather common sense approach, isn't it?
Problem 10.
In an isosceles right $\triangle ABC$, $\angle C=90^0$. If $D$ is any point on $AB$ then $AB^2+BD^2$ is equal to,
- $2CD^2$
- $4CD^2$
- $3CD^2$
- $CD^2$
Solution 10: Problem analysis
The following is the visualization relevant to the problem.

$\triangle ABC$ being isosceles with $AC=BC$, the perpendicular $CE$ dropped from $C$ to $AB$ bisects $AB$ at $E$. Let $AE=BE=a$, $DE=b$.
Essentially then,
$AD^2 +BD^2=(a+b)^2+(a-b)^2=2(a^2+b^2)$, $2ab$ cancel out. This algebraic simplification is the first key pattern identification.
Dropping the perpendicular bisector $CE$ is visualization by indroducing a new element. This decision was made by foreseeing the simplification of $2ab$ cancelling out.
Now we identify the second key pattern of $CE$ as the angle bisector of $\angle C$, so that both triangles $\triangle BEC$ and $\triangle AEC$ turn out to be isosceles.
Reason: In the two triangles $\triangle AEC$ and $\triangle BEC$, by problem statement, $\angle CAE=\angle CBE$ and the other pair of angles are both $90^0$. So the third pair of angles,
$\angle ACE=\angle BCE=45^0$, as $\angle ACB=90^0$.
As by problem statement, in the isosceles right triangle $\triangle ABC$, $\angle ABC=\angle BAC=45^0$, the two triangles, $\triangle AEC$ and $\triangle BEC$ are both isosceles.
This makes $AE=BE=CE=a$.
Thus,
$AD^2+BD^2=2a^2+2b^2$,
$=2a^2+2CD^2-2CE^2$,
$=2CD^2$, as $CE=a$.
Answer: Option a: $2CD^2$.
Unless you can visualize and identify the key patterns in two stages, solution cannot be reached so quickly.
Key concepts used: Visualization -- Algebraic simplification -- Key pattern identification in two stages -- Pythagoras theorem -- Property of perpendicular bisector of an isosceles triangle from the vertex bisecting the vertex angle -- Properties of right angled isosceles triangles.
Note: Though this problem looks simple, it needs application of a number of rich concepts and key pattern identifications. Additionally it needs algebraic concepts.
Guided help on Geometry in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Geometry in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Geometry and relevant topics in Suresolv and is up-to-date.