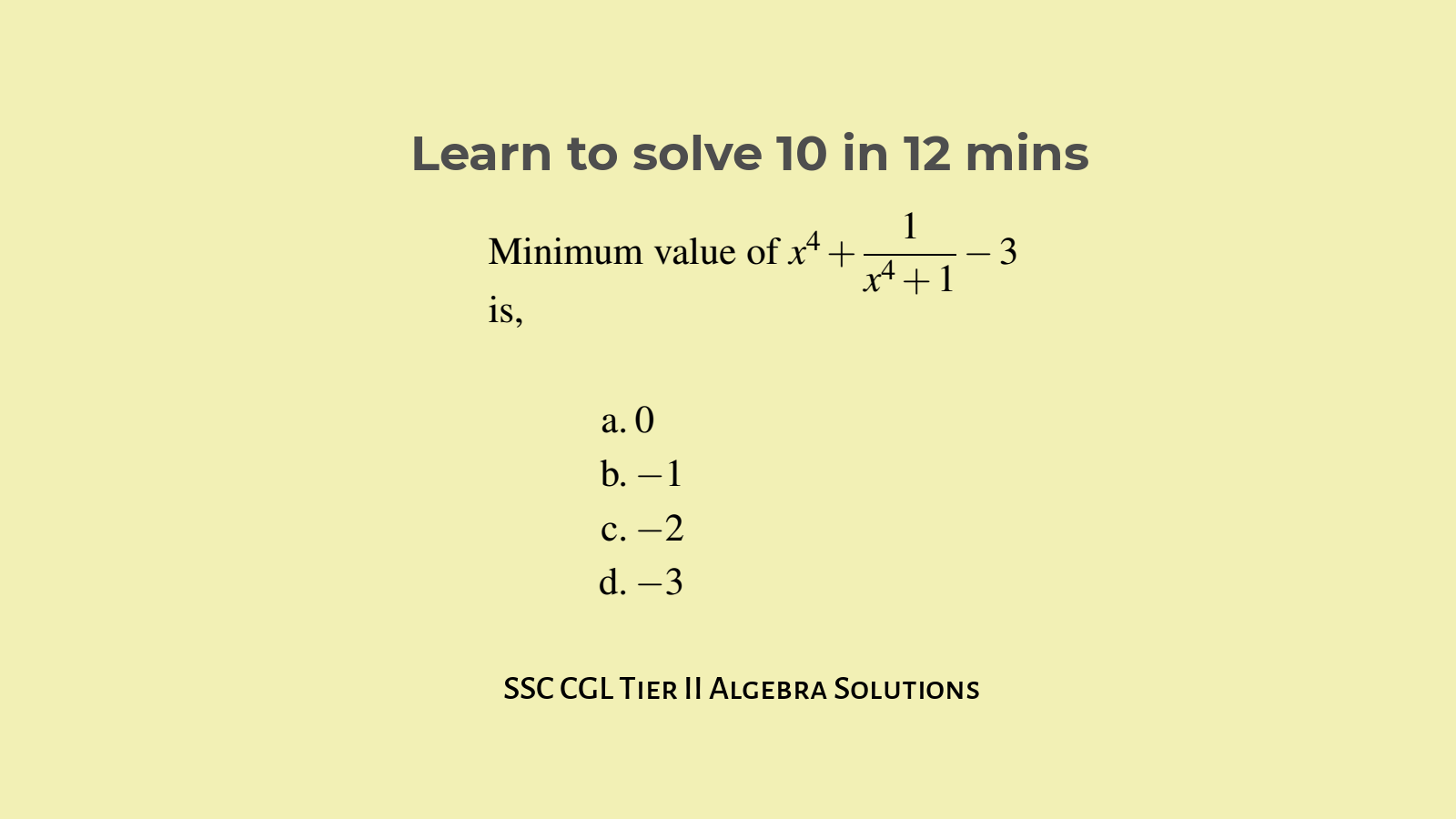
Solution Set 3 on Algebra for SSC CGL Tier 2
Learn how to solve the Set 3 of Algebra questions for SSC CGL Tier 2 quickly using basic and advanced algebra problem solving techniques.
If you have not yet taken this test you may take it by referring to the SSC CGL Tier II level question set 3 on Algebra 3 before going through the solution.
Algebra solutions for SSC CGL Tier 2 Set 3 - answering time was 12 mins
Q1. If $4y-3x=13$ and $xy=14$, then $64y^3-27x^3$ is,
- 8479
- 8400
- 8740
- 8749
Solution 1 - Problem analysis and execution
As the target expression is a sum of cubes of the terms in the given expression we need to use the factored form of the target expression as,
$p^3-q^3=(p-q)(p^2+pq+q^2)$, where $p=4y$ and $q=3x$.
We know $p-q=13$, and $pq=12xy=168$ is also now known.
By raising the given equation to its square we would be able to evaluate, $(p^2+pq+q^2)$ and so also $p^3-q^3$.
Replacing $4y$ by $p$ and $3x$ by $q$ simplifies written or mental deduction saving precious time. This is use of Abstraction and Substitution techniques resulting in useful problem transformation.
Solution 1 - Problem solving execution
$4y-3x=13$,
Or, $(p-q)^2 = p^2-2pq+q^2=169$,
Or, $p^2+pq+q^2=169+3pq$, the term $3pq$ added to both sides,
Or, $p^2+pq+q^2=169+504=673$.
So,
$64y^3-27x^3=p^3-q^3$
$=(p-q)(p^2+pq+q^2)$
$=13\times{673}$
$=8749$.
Answer: Option d: 8749.
Note: Both the calculations can be carried out mentally, but if you are in any doubt, do it by hand. Use of abstraction and substitution of $4y$ and $3x$ by $p$ and $q$ respectively not only reduces the memory load of remembering and manipulating $4y$ and $3x$, it also increases comfort in dealing with familiar form of factored sum of cubes in two unit-coefficient variables $p$ and $q$. In pressure situation these steps improve the speed and accuracy.
Key concepts used: Abstraction -- Substitution -- factorization of sum of cubes.
Q2. If $x=(0.09)^2$, $y=\displaystyle\frac{1}{(0.09)^2}$ and $z=(1- 0.09)^2 - 1$, then which of the following relations is true?,
- $y \lt x$ and $x=z$
- $y \lt z \lt x$
- $z \lt x \lt y$
- $x \lt y$ and $x=z$
Solution 2 - Problem analysis
Noticing that $0.09$ appears throughout the given expressions, instead of calculating the values of terms involving $0.09$ we will abstract and substitute $0.09$ by a constant $p \lt 1$ and then only resort to comparison of $x$, $y$ and $z$.
Solution 2 - Problem solving execution
By substitution, $p=0.09$, where $p \lt 1$ we have the transformed given equations as,
$x=p^2$,
$y=\displaystyle\frac{1}{p^2}$, and
$z=(1-p)^2-1=p^2 - 2p$.
When comparing $x$ with $y$ we can conclude that,
$y \gt x$, as $p \lt 1$ (dividing 1 by a value less than 1 makes $y$ larger than 1, whereas $x$ is less than 1).
Comparing $x$ with $z$ we can conclude that,
$x \gt z$, as $p$ is positive.
These two conclusions are sufficient to finally form the desired comparative relation between the three variables as,
$y \gt x \gt z$,
Or, $z \lt x \lt y$.
Answer: Option c : $z \lt x \lt y$.
Key concepts used: Abstraction and substitution with a view to eliminate calculation -- efficient simplification -- expression value comparison -- joining two inequalities to arrive as the desired comparative relation -- inequality analysis -- problem generalization.
Note: The value of $p$ need only be less than 1 to arrive at the same relation between $x$, $y$ and $z$ as above; value of $p$ can very well be $.3$, $0.001$ or $.99$ without changing the above process and solution in any way. This is the power of abstraction and problem generalization. It not only saves you precious time to reach your solution but also makes you aware of many other similar problems that can be solved in similar way.
Q3. Minimum value of $x^4 +\displaystyle\frac{1}{x^4+1} - 3$ is,
- $0$
- $-1$
- $-2$
- $-3$
Solution 3 - Problem analysis
We can see from the form of the target expression that it can easily be converted to a sum of inverses $p+\displaystyle\frac{1}{p}$, where $p=x^4+1$. As we know that the minima of sum of inverses gives minimum value of sum of inverses as $2$ the actual solution is only a step away.
Solution 3 - Problem solving execution
The target expression is then expressed as,
$E=x^4 +\displaystyle\frac{1}{x^4+1} - 3$
$\hspace{5mm}=(x^4+1)+\displaystyle\frac{1}{(x^4+1)} - 4$
$\hspace{5mm}=p+\displaystyle\frac{1}{p} - 4$, where $p=x^4+1$
$\hspace{5mm}=E_1-4$, where $E_1=p+\displaystyle\frac{1}{p}$.
By applying minima of sum inverses concept we get the minimum value of $E_1$ as 2,
So the minimum value of the target expression $E$ is,
$2-4=-2$.
Answer: Option c: $-2$.
Key concepts used: Key pattern identification -- Abstraction -- substitution -- input transformation -- minima of sum of inverses concept -- problem generalization.
Note: Firstly, we are not repeating here the minima of sum of inverses mechanism. You may refer to the mechanism either in SSC CGL Tier II level Solution Set 1, Algebra 1, or SSC CGL Tier II level Solution Set 2, Algebra 2.
Secondly, because of the abstraction and substitution of $x^4+1$ by $p$, we can now be aware that whatever be the nature of the expression $x^4+1$, if it appears in sum of inverses form, we can always find the minima of the resulting expression. For example, the minima of the expression, $x^{99}+\displaystyle\frac{1}{x^{99}+1} -3$ would have been exactly the same value as the given expression in this problem. This is problem generalization.
Q4. If $\displaystyle\frac{p}{3}=\frac{q}{2}$ then the value of $\displaystyle\frac{2p+3q}{3p-2q}$ is,
- $1$
- $\displaystyle\frac{12}{5}$
- $\displaystyle\frac{5}{12}$
- $\displaystyle\frac{12}{7}$
Solution 4 - Problem analysis
It becomes apparent on a quick examination of the given expression that we will immediately get the useful value,
$\displaystyle\frac{p}{q}=\frac{3}{2}$.
To evaluate the target expression, as we need to use this value of $\displaystyle\frac{p}{q}$, for efficient simplification with least chances of error, we will factor out $3q$ from the numerator and $2q$ from the denominator so that firstly $q$ gets canceled out and secondly each of the expressions gets simplified with one of the two terms transformed to $1$.
Solution 4 - Problem solving execution
Evaluating the target expression we get,
$E=\displaystyle\frac{2p+3q}{3p-2q}$
$\hspace{5mm}=\displaystyle\frac{3q}{2q}\times{\displaystyle\frac{\displaystyle\frac{2p}{3q}+1}{\displaystyle\frac{3p}{2q}-1}}$
$\hspace{5mm}=\displaystyle\frac{3}{2}\times{\displaystyle\frac{1+1}{\displaystyle\frac{9}{4}-1}}$
$\hspace{5mm}=\displaystyle\frac{3}{2}\times{\displaystyle\frac{2}{\displaystyle\frac{5}{4}}}$
$\hspace{5mm}=\displaystyle\frac{3}{2}\times{\displaystyle\frac{8}{5}}$
$\hspace{5mm}=\displaystyle\frac{12}{5}$.
Answer: Option b: $\displaystyle\frac{12}{5}$.
Key concepts used: Input transformation -- substitution -- efficient simplification.
Q5. If $(a-4)^2 + (b-9)^2+(c-3)^2=0$, then the value of $\sqrt{a+b+c}$ is,
- $\pm{4}$
- $4$
- $-4$
- $\pm{2}$
Solution 5 - Problem analysis and execution
By the principle of zero sum of square terms, when all the terms in an additive expression equated to zero are square terms, each of the terms must be zero for the equation to be valid. This happens because each of the squares, if non-zero, will be positive resulting in a non-zero positive result on summation which will violate its zero sum status.
So in our given problem we have,
$(a-4)=0$,
Or, $a=4$.
$(b-9)=0$,
Or, $b=9$, and
$(c-3)=0$,
Or, $c=3$.
Thus target expression is,
$E=\sqrt{a+b+c}=\sqrt{16}=4$.
Answer: Option b: 4.
Key concepts used: Principle of zero sum of square terms -- square root concept.
Note: Mathematically the square root function returns a positive output. It cannot be negative, and so $\sqrt{16} \neq -4$. The square of $\pm{4}=16$ converting the negative in the input to a positive because of double multiplication of a factor $-1$. One can question, what will be the square root expression when the output result is $-4$? It will simply be, $-4=-\sqrt{16}$.
Q6. If $\displaystyle\frac{1}{x+y}=\displaystyle\frac{1}x+\displaystyle\frac{1}{y}$, where, $x \neq 0$, $y \neq 0$ and $x \neq y$, the value of $x^3-y^3$ is,
- $0$
- $2$
- $1$
- $-1$
Solution 6 - Problem analysis
As the target expression is a subtractive sum of cubes, we will get its value if we have the values of its two factors in its expanded form,
$x^3-y^3=(x-y)(x^2+xy+y^2)$.
We need to manipulate the given expression to get an idea of the values of either or both of these two factors.
Solution 6 - Problem solving execution
The given equation is,
$\displaystyle\frac{1}{x+y}=\displaystyle\frac{1}x+\displaystyle\frac{1}{y}$
Multiplying both sides by $xy$,
$\displaystyle\frac{xy}{x+y}=x+y$
Or, $xy=(x+y)^2$,
Or, $x^2+xy+y^2=0$.
This is the second factor in target expression so that target expression evaluates finally to $0$.
Answer: Option a : 0.
Key concepts used: Input transformation -- factorization of subtractive sum of cubes.
Q7. If $a^x=(x+y+z)^y$, $a^y=(x+y+z)^z$ and $a^z=(x+y+z)^x$ find the value of $a+b+c$ where $a \neq 0$.
- $0$
- $1$
- $a^3$
- $a$
Solution 7 - Problem analysis and execution
On analyzing the three expressions we discover the key pattern of base equalization, and decide to multiply the three expressions together giving,
$a^x.a^y.a^z=(x+y+z)^{x+y+z}$,
Or, $a^{x+y+z}=(x+y+z)^{x+y+z}$.
Here the equalized base is the power and not the indice base.
So the indice bases are equal, or,
$x+y+z=a$.
Answer: Option d: $a$.
Key concepts used: Key pattern identification -- Base equalization technique -- principle of collection of friendly terms -- indices concepts.
Note: Here we have used principle of collection of friendly terms multiplicatively and not additively which we usually do. Being abstract, the principle comes to be useful for multplicative use also.
Q8. If $\displaystyle\frac{x-a^2}{b^2+c^2} + \displaystyle\frac{x-b^2}{c^2+a^2} +\displaystyle\frac{x-c^2}{a^2+b^2} =3$ then the value of $x$ is,
- $a^2+b^2$
- $a^2+b^2+c^2$
- $a^2+b^2-c^2$
- $a^2-b^2-c^2$
Solution 8 - Problem analysis:
We identify the key pattern that each of the three fraction terms contains $a^2$, $b^2$ and $c^2$ in numerator and denominator combined. In the second pass we also recognize that we need only to subtract 1 from each of the fraction terms to create the expression $\left(x-(a^2+b^2+c^2)\right)$ in each numerator.
But from where would we get the three 1s to be subtracted from the three terms on the LHS? Easy. Just split the $3$ on the RHS into three 1s and use each on the LHS.
As a result we would get the expression, $\left(x-(a^2+b^2+c^2)\right)$ as a factor of an equation equated to 0. This makes the factor itself 0, giving $x=a^2+b^2+c^2$.
It is all done in mind using key pattern identification and principle of collection of friendly terms.
Let us show how this actually happens.
Solution 8 - Problem solving execution
We have the given equation as,
$\displaystyle\frac{x-a^2}{b^2+c^2} + \displaystyle\frac{x-b^2}{c^2+a^2} +\displaystyle\frac{x-c^2}{a^2+b^2} =3$,
Or, $(x-a^2-b^2-c^2)\times{\left(\displaystyle\frac{1}{b^2+c^2}+\displaystyle\frac{1}{c^2+a^2}+\displaystyle\frac{1}{a^2+b^2}\right)}=0$.
So $x-a^2-b^2-c^2=0$,
Or, $x=a^2+b^2+c^2$.
Answer: Option b: $a^2+b^2+c^2$.
Key concepts used: Key pattern identification -- principle of collection of friendly terms -- simplification.
Q9. If $ax^2+bx+c=a(x-p)^2$, then the correct relation between $a$, $b$ and $c$ would be,
- $2b=a+c$
- $b^2=4ac$
- $b^2=ac$
- $abc=1$
Solution 9 - Problem analysis
The only promising course of action seems to be expanding the RHS and equating coefficients of like terms between LHS and RHS.
Solution 9 - Problem solving execution
Expanding the RHS of the given expression we have,
$ax^2+bx+c=a(x-p)^2$,
Or, $ax^2+bx+c=ax^2 -2apx +ap^2$.
Equating the coefficients of like terms on the two sides of the equation we get,
$b=-2ap$, and
$c=ap^2$.
We will now raise the first equation to a square and divide the two equations with each other to eliminate $p$ leaving only $a$, $b$ and $c$.
$b=-2ap$,
Or, $b^2=4a^2p^2$.
Dividing this equation by the second equation, $c=ap^2$ we get,
$\displaystyle\frac{b^2}{c}=4a$,
Or, $b^2=4ac$.
Ans: Option b: $b^2=4ac$.
Key concepts used: Coefficient comparison technique -- variable elimination technique.
Q10. If $\displaystyle\frac{y}{x} - \displaystyle\frac{x}{y}=3$, then find the value of $\displaystyle\frac{x^3}{y^3} + \displaystyle\frac{y^3}{x^3}$.
- $10\sqrt{3}$
- $10\sqrt{13}$
- $13\sqrt{3}$
- $13\sqrt{10}$
Solution 10 - Problem analysis
The very first thing we notice is the occurrence of only $\displaystyle\frac{y}{x}$ and $\displaystyle\frac{x}{y}$ like independent variables in the given as well as the target expression. Taking this opportunity we decide to use abstraction and variable substitution techniques to replace these two by $p$ and $\displaystyle\frac{1}{p}$ respectively.
By these two substitutions of $p=\displaystyle\frac{y}{x}$ and $\displaystyle\frac{1}{p}=\frac{x}{y}$, the given expression is transformed to,
$p-\displaystyle\frac{1}{p}=3$.
Similarly the target expression is transformed to,
$E=p^3+\displaystyle\frac{1}{p^3}$.
By this simple action we have transformed the problem to a problem involving pure sum of inverses.
As the input is in the form of subtractive sum of inverses while the target is in the form of additive sum of inverses of cubes, we need first to evaluate the additive form of the sum of inverses from the given equation.
Solution 10 - Problem solving execution
Raising the given equation to a power of 2,
$p^2-2+\displaystyle\frac{1}{p^2}=9$,
Or, $p^2+2+\displaystyle\frac{1}{p^2}=9+4=13$,
Or, $\left(p+\displaystyle\frac{1}{p}\right)^2=13$,
Or, $\left(p+\displaystyle\frac{1}{p}\right)=\sqrt{13}$.
Again from the square of the given expression we have,
$p^2-2+\displaystyle\frac{1}{p^2}=9$,
Or, $p^2-1+\displaystyle\frac{1}{p^2}=10$.
This is the second factor of the target cubes expression expanded. So we have the target expression as,
$E=p^3+\displaystyle\frac{1}{p^3}$,
$\hspace{5mm}=\left(p+\displaystyle\frac{1}{p}\right)\left(p^2-1+\displaystyle\frac{1}{p^2}\right)$
$\hspace{5mm}=\sqrt{13}\times{10}=10\sqrt{13}$
Answer: Option b: $10\sqrt{13}$.
Key concepts used: Abstraction -- Substitution -- principle of interaction of inverses -- factorization of sum of cubes -- multiple input use technique -- efficient simplification -- intermediate result use.
Note: We have used the input expression in multiple ways to generate the two factors of the target expression. This is multiple input use technique in action.
Also practicing efficient simplification, when evaluating the second factor, we have not started by squaring the given expression; rather we have used the already available result of $p^2-2-\displaystyle\frac{1}{p^2}=9$. This practice saves precious seconds in a high end competitive exam increasing your score and chances of success.
Efficient simplification is not just one technique. It is a collection of a host of techniques each saving seconds in reaching the solution at the stage of simplification.
This concept works at the last layer of problem solving. In this case, the specific variation of the concept of efficient simplification is the technique of intermediate result use. This is a type of efficient simplification and hence is a subconcept of the parent concept efficient simplification. This is called concept hierarchy or concept structure.
Lastly intermediate result use and intermediate expression use differ in that, the intermediate expression use works at a higher level and helps in transforming the problem itself.
Guided help on Algebra in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Algebra in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Algebra in Suresolv and is up-to-date.