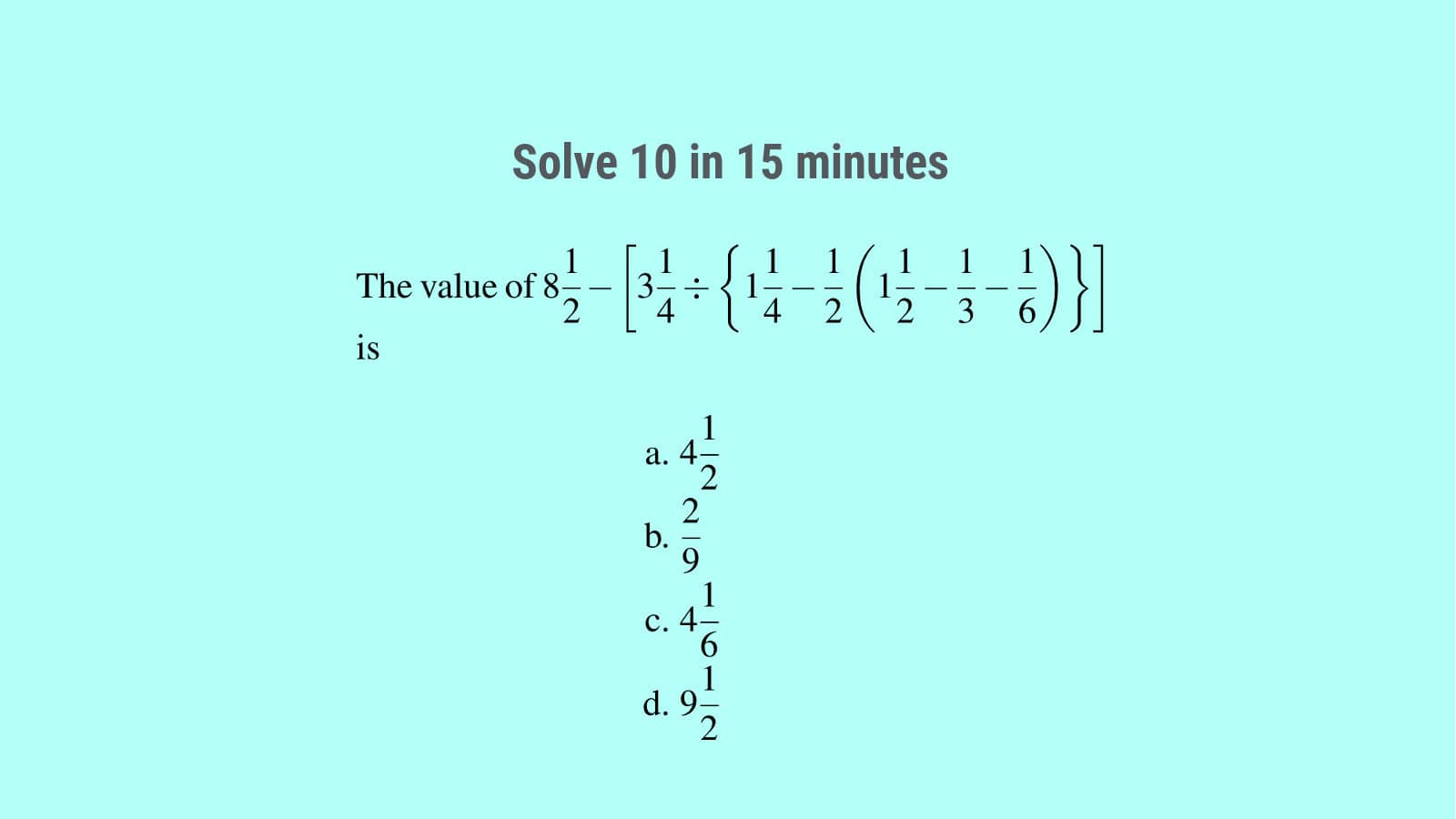
Fraction decimal questions SSC CGL Set 75
10 Selected fraction decimal questions for SSC CGL Set 75 to solve in 15 minutes. Verify correctness from answers. Learn to solve from solutions.
Contents are,
- Fraction questions for SSC CGL.
- Decimal questions for SSC CGL.
- Indices questions for SSC CGL.
- Answer to the 10 questions.
Answer and link to the solutions are at the end.
Fraction decimal questions for SSC CGL Set 75 - time to solve 15 mins
Problem 1.
$\displaystyle\frac{13}{48}$ is equal to,
- $\displaystyle\frac{1}{3+\displaystyle\frac{1}{1+\displaystyle\frac{1}{16}}}$
- $\displaystyle\frac{1}{3+\displaystyle\frac{1}{1+\displaystyle\frac{1}{1+\displaystyle\frac{1}{8}}}}$
- $\displaystyle\frac{1}{2+\displaystyle\frac{1}{1+\displaystyle\frac{1}{8}}}$
- $\displaystyle\frac{1}{3+\displaystyle\frac{1}{1+\displaystyle\frac{1}{2+\displaystyle\frac{1}{4}}}}$
Problem 2.
When $\left(\displaystyle\frac{1}{2} -\displaystyle\frac{1}{4}+\displaystyle\frac{1}{5}-\displaystyle\frac{1}{6}\right)$ is divided by $\left(\displaystyle\frac{2}{5} -\displaystyle\frac{5}{9}+\displaystyle\frac{3}{5}-\displaystyle\frac{7}{18}\right)$ the result is,
- $5\displaystyle\frac{1}{10}$
- $3\displaystyle\frac{1}{6}$
- $3\displaystyle\frac{3}{10}$
- $2\displaystyle\frac{1}{18}$
Problem 3.
On simplification, $3034-(1002\div{20.04})$ is equal to,
- $2993$
- $2984$
- $3029$
- $2543$
Problem 4.
Value of $\displaystyle\frac{\displaystyle\frac{5}{3}\times{\displaystyle\frac{7}{51}}\text{ of }\displaystyle\frac{17}{5}-\displaystyle\frac{1}{3}}{\displaystyle\frac{2}{9}\times{\displaystyle\frac{5}{7}}\text{ of }\displaystyle\frac{28}{5}-\displaystyle\frac{2}{3}}$ is,
- $\displaystyle\frac{1}{2}$
- $4$
- $\displaystyle\frac{1}{4}$
- $2$
Problem 5.
Value of $\displaystyle\frac{9|3-5|-5|4|\div{10}}{-3(5)-2\times{4}\div{2}}$ is,
- $\displaystyle\frac{9}{10}$
- $\displaystyle\frac{4}{7}$
- $-\displaystyle\frac{8}{17}$
- $-\displaystyle\frac{16}{19}$
Problem 6.
The value of
$\left(1+\displaystyle\frac{1}{10+\displaystyle\frac{1}{10}}\right)\left(1+\displaystyle\frac{1}{10+\displaystyle\frac{1}{10}}\right)-$
$\left(1-\displaystyle\frac{1}{10+\displaystyle\frac{1}{10}}\right)\left(1-\displaystyle\frac{1}{10+\displaystyle\frac{1}{10}}\right)$ ÷
$\left[\left(1+\displaystyle\frac{1}{10+\displaystyle\frac{1}{10}}\right)-\left(1-\displaystyle\frac{1}{10+\displaystyle\frac{1}{10}}\right)\right]$ is,
- $2$
- $\displaystyle\frac{90}{101}$
- $\displaystyle\frac{20}{101}$
- $\displaystyle\frac{100}{101}$
Problem 7.
The value of $8\displaystyle\frac{1}{2}-\left[3\displaystyle\frac{1}{4}\div{\left\{1\displaystyle\frac{1}{4}-\displaystyle\frac{1}{2}\left(1\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}-\displaystyle\frac{1}{6}\right)\right\}}\right]$ is
- $4\displaystyle\frac{1}{2}$
- $\displaystyle\frac{2}{9}$
- $4\displaystyle\frac{1}{6}$
- $9\displaystyle\frac{1}{2}$
Problem 8.
$\sqrt{\displaystyle\frac{4\displaystyle\frac{1}{7}-2\displaystyle\frac{1}{4}}{3\displaystyle\frac{1}{2}+1\displaystyle\frac{1}{7}}\div{\displaystyle\frac{1}{2+\displaystyle\frac{1}{2+\displaystyle\frac{1}{5-\displaystyle\frac{1}{5}}}}}}$ is equal to,
- $1$
- $2$
- $3$
- $4$
Problem 9.
The value of $\displaystyle\frac{1+\displaystyle\frac{1}{2}}{1-\displaystyle\frac{1}{2}}\div{\displaystyle\frac{4}{7}\left(\displaystyle\frac{2}{5}+\displaystyle\frac{3}{10}\right)}\text { of }\displaystyle\frac{\displaystyle\frac{1}{2}+\displaystyle\frac{1}{3}}{\displaystyle\frac{1}{2}-\displaystyle\frac{1}{3}}$ is,
- $37\displaystyle\frac{1}{2}$
- $18\displaystyle\frac{3}{8}$
- $\displaystyle\frac{3}{2}$
- $\displaystyle\frac{2}{3}$
Problem 10.
When simplified, the expression $(100)^{\frac{1}{2}}\times{(0.001)^{\frac{1}{3}}}-(0.0016)^{\frac{1}{4}}\times{3^0}+\left(\displaystyle\frac{5}{4}\right)^{-1}$ is equal to,
- $1.0$
- $1.6$
- $0$
- $0.8$
You may refer to the corresponding solution set, SSC CGL Solution Set 75 on Fractions decimals and indices 7, where we have applied special time-saving techniques and methods to quickly solve the problems in mind as far as possible.
The answers to the questions are given below followed by a list of relevant articles of concept tutorials, question and solution sets.
Answers to the fraction decimal questions SSC CGL Set 75
Problem 1. Answer: Option d: $\displaystyle\frac{1}{3+\displaystyle\frac{1}{1+\displaystyle\frac{1}{2+\displaystyle\frac{1}{4}}}}$.
Problem 2. Answer. Option a: $5\displaystyle\frac{1}{10}$.
Problem 3. Answer: Option b. 2984.
Problem 4. Answer: Option d: $2$.
Problem 5. Answer: Option d: $-\displaystyle\frac{16}{19}$.
Problem 6. Answer: Option a: $2$.
Problem 7. Answer: Option c: $4\displaystyle\frac{1}{6}$.
Problem 8. Answer: Option a: 1.
Problem 9. Answer. Option a: $37\displaystyle\frac{1}{2}$.
Problem 10. Answer: Option b: $1.6$.
Guided help on Fractions, Surds and Indices in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on fractions, surds and indices in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Fractions, Surds and Indices and relevant topics in Suresolv and is up-to-date.