
Ratio and percentage questions SSC CGL Set 25 with solutions
Learn to solve quickly 10 Ratio and percentage questions in SSC CGL Set 25. For quick solutions basic and advanced ratio and percentage concepts used.
To know how to confidently solve a few of the tricky questions, go through the solutions carefully.
For best results take the test first at,
SSC CGL Question Set 25, Arithmetic Percentage, Ratio and Proportion 4.
Solutions to 10 Ratio and percentage questions SSC CGL Set 25 - Answering time was 12 mins
Problem 1.
Dry grapes contain 10% water while fresh grapes contain 80% water. What will be the weight (in kg) of fresh grapes when it weighs 50 kg as dry?
- 208
- 225
- 235
- 215
Solution 1 - Problem analysis
This is a special type of mixing problem in which water is mixed homogeneously throughout the grapes. As usual two event states are given between which the percentage of water changes with weight of grape mass remaining constant. When drying, the water evaporates but the grape mass weight remains unchanged. With this basic concept of the problem model in place we will try to reach the solution in a few steps.
Solution 1 - Problem solving execution
When dry, 1 kg of grape contains 10% or 0.1 kg of water,
So, 50 kg of dry grape will contain 5kg of water, that is, $(50-5)=45$ kg of grape mass without water.
When fresh,
20% of total weight of the fresh grapes = this grape mass of 45 kg,
and rest 80% water.
So when fresh,
100% of total weight of fresh grapes = $5\times{45} = 225$ kg, 20% is one-fifth, so 100% is five times.
Answer: Option b: 225.
Key concepts used: Understanding the problem in terms of grape mass remaining unchanged in weight and only water changing in weight due to evaporation thus decreasing the wight when grapes get dry from fresh state -- from water percentage in dry grapes, directly obtaining the grape mass that remains unchanged even in fresh grapes -- transforming this grape mass to total fresh grape weight by grape mass percentage relation -- following the shortest path to the solution.
Problem 2.
Full tank petrol for Vijay's mobike lasts for 20 days. How many days a full tank will last for him if he increases his daily consumption of petrol by 25%?
- 16
- 10
- 12
- 14
Solution 2 - Problem analysis
Let the original per day consumption of petrol by Vijay be $C$. So his total consumption in 20 days was, $20C$ which is the capacity of the tank.
On increase of rate of consumption by 25%, the per day consumption now is, $1.25C$. With this consumption rate if the full tank petrol lasts for $D$ number of days, we have,
$1.25CD = 20C$,
Or, $D = \displaystyle\frac{20}{1.25} = 16$.
Answer: Option a : 16.
Key concepts used: Deducing the full tank capacity in terms of Vijay's original rate of petrol consumption and equating it with increased rate of consumption per day multiplied by the number of days -- the rate of consumption is canceled out in the equation as it is in percent increase.
Problem 3.
Number of students in three classes $A$, $B$ and $C$ in a school were in a ratio $2 : 3 : 4$ in last year. This year the numbers increased by certain percentages to change the ratio to $11 : 18 : 26$. If the percentage increase in class $C$ were 30% what is the percentage increase in class $B$?
- 25%
- 20%
- 10%
- 15%
Solution 3 - Problem analysis
As a first step we reintroduce the common HCF canceled out between the first ratio terms as $x$ so that the ratio is transformed to ratio of actual numbers,
$2x : 3x : 4x$, where the three terms are now the actual numbers of students.
Similarly, after the increase of the individual numbers by certain percentages the changed ratio is expressed as,
$11y : 18y : 26y$.
The common factor $x$ will no longer be the same as the new canceled out HCF of the second ratio $y$.
It won't have been otherwise possible to deduce the relation between $x$ and $y$ and hence the percent increases for all three numbers unless a key information were provided. The percent increase in number of students in class $C$ is this key information.
Solution 3 - Problem solving execution
By the problem statement,
$(4 + 0.3\times{4})x = 26y$,
Or, $5.2x = 26y$,
Or, $y = 0.2x$.
As, increased number in class $B$ is,
$18y = 18\times{0.2x} = 3.6x$,
the increase of number of students in class $B$ is,
$3.6x - 3x = 0.6x$, which is a 20% increase of $3x$, (one-fifth of 3).
Answer: Option b: 20%.
Key concepts used: Reintroducing the HCF of both the ratios to get the actual numbers before and after in terms of unknowns $x$ and $y$ -- establishing the relation between $x$ and $y$ by the percent increase data for class $C$ and then deducing the actual value in terms of $x$ for class $B$ to get the percent increase.
Problem 4.
Due to price rise of rice by 25% per kg Labanya could only purchase 20 kg less than what she had purchased at the expense of Rs.400 before the price rise. The increase in price of rice per kg (in Rs.) is,
- 2
- 1.5
- 1
- 3
Solution 4 - Problem analysis
In a purchase, the relation between price, purchased quantity and total cost of purchase is,
$P\times{Q} = C$, where $P$ is per unit cost or the price, $Q$ is the quantity purchased and $C$ is the total cost of purchase.
If the total cost remains unchanged but the other two change, we say, price is inversely proportional to the quantity purchased in same amount of total cost. We express this as,
$Q= C\displaystyle\frac{1}{P}$.
It means, if price increases purchased quantity decrease and vice versa with money to purchase remaining same.
In this prolem, as price has increased by 25% it has become $1.25P$, if $P$ were the original price.
So,
$Q_2 = C\displaystyle\frac{1}{1.25P} = C\displaystyle\frac{4}{5P}$, whereas, before the price rise, the quantity that could be purchased was,
$Q = C\displaystyle\frac{1}{P}$.
Thus,
$Q_2 = \displaystyle\frac{4}{5}Q = 0.8Q$.
It means, if the total cost remains unchanged, for a price rise of 25%, purchasable quantity reduces by a fixed percent of 20% whatever be the total funds or cost of purchase.
This is for clarifying the basic concept and also for use in problem solving.
Solution 4 - Problem solving execution
Thus, 20 kg less quantity purchased due to price rise is equivalent to 20% of original quantity, which would then be,
$5\times{20} = 100kg$, (100% is five times 20%, and represents the whole amount)
So original price = $\displaystyle\frac{400}{100} = 4$ in Rs. per kg and 25% or one-fourth increase of it is, Rs 1 per kg.
Answer: Option c: 1.
Key concepts used: From the basic proportionality relation between price and quantity cost remaining fixed, derivation of original quantity -- this gave us original price and the percent increase gave us the actual increase.
Problem 5.
Two vessels A and B of equal capacity of 5 litres each are filled with milk and water respectively. If 20% of water is taken out from vessel B, mixed thoroughly in vessel A and then again 20% of the mixture in vessel A is taken out and mixed back into vessel B thoroughly, the relation between the volume of water in milk vessel A and volume of milk in water vessel B is,
- Water in $A$ = Milk in $B$
- Water in $A$ $\lt$ Milk in $B$
- Water in $A$ $\gt$ Milk in $B$
- cannot be answered with the given information
Solution 5 - Problem analysis
This is apparently a liquid mixing problem of a special type that can be solved easily by calculating the requisite portions of milk and water in the exchange.
On looking at the problem closer we find that in the first operation 1 litre water is taken out of vessel B and mixed in 5 litre of vessel A, trying to make the volume of liquid 6 litres in a 5 litre vessel.
It means there will be an overflow in vessel A and the volumes of liquids will be uncertain. Thus the answer cannot be given with the information available.
Answer: Option d: cannot be answered with the given information.
Key concept used: Awareness of context.
Problem 6.
As the price of oil has increased by 32%, a family has managed to decrease its oil consumption in such a way that effective increase in oil price was only 10% for them. If oil consumption were 10 litres before the price rise, what is the consumption (in litres) now?
- 9
- $8\displaystyle\frac{1}{3}$
- $8\displaystyle\frac{3}{4}$
- $8\displaystyle\frac{1}{2}$
Solution 6 - Problem analysis
The same basic relation between quantity or consumption, price and cost holds in this case. Quantity $Q$ purchased at price per unit $P$ and at a total cost $C$ is,
$Q = \displaystyle\frac{C}{P}$.
We need to use this relation for solving our problem.
Solution 6 - Problem solving execution
Before the price rise the expense was,
$C_1 = 10P$, where 10 litres was the consumption and $P$ per litre was the price.
The family reduced consumption in such a way that effective price rise was 10%. This means, total cost increased by 10%, that is, it became $11P$.
So, after the price rise by 32% price $P$ becoming $1.32P$,
$1.32P\times{Q_2} = 11P$,
Or, $Q_2 = \displaystyle\frac{11}{1.32}=\frac{100}{12}=8\frac{1}{3}$ litres.
Answer: Option b : $8\displaystyle\frac{1}{3}$.
Key concepts used: Basic purchase price, cost and quantity proportionality concept.
Problem 7.
A box has 100 red balls, 50 blue balls and 50 black balls. 50% of the blue balls and 25% of the red balls were taken out of the box. What is the percentage of black balls in the box now?
- 25%
- 50%
- $33\displaystyle\frac{1}{3}$%
- 40%
Solution 7 - Problem analysis
50% of blue balls, that is, one-half of 50, which is 25; 25% of red balls, that is one-fourth of 100, which is 25, a total of 50 balls are taken out from 200.
So 50 black balls remains out of 150, that is one-third, a percentage equivalence of $33\displaystyle\frac{1}{3}$%.
Answer: c: $33\displaystyle\frac{1}{3}$%
Key concepts used: Basic percent concepts.
Problem 8.
If 4 litres of water is mixed with a 20 litres of mixture of water and alcohol of 20% alchohol strength, what will be the percentage strength of alcohol after mixing?
- $33\displaystyle\frac{1}{3}$%
- $12\displaystyle\frac{1}{2}$%
- $16\displaystyle\frac{2}{3}$%
- 25%
Solution 8 - Problem analysis
20% alchohol in 20 litres mixture equals 4 litres of alchohol (one-fifth of 20).
When 4 litres of water is added total volume changes to 24 litres out of which 4 litres is alcohol which is a percent of,
$\displaystyle\frac{4}{24}\times{100}=16\displaystyle\frac{2}{3}$% alcohol.
Answer: Option c: $16\displaystyle\frac{2}{3}$%.
Key concepts used: Basic percent concepts.
Problem 9.
If the numerator of a fraction is increased by 20% and the denominator is decreased by 5% then the new fraction becomes $\displaystyle\frac{5}{2}$. The original fraction was,
- $\displaystyle\frac{24}{19}$
- $\displaystyle\frac{3}{18}$
- $\displaystyle\frac{48}{95}$
- $\displaystyle\frac{95}{48}$
Solution 9 - Problem analysis
Assuming the original fraction as $\displaystyle\frac{N}{D}$, after the change in values,
$\displaystyle\frac{1.2N}{0.95D} = \frac{5}{2}$,
Or, $\displaystyle\frac{N}{D} = \frac{5\times{0.95}}{2\times{1.2}}=\frac{95}{48}$.
Answer: Option d: $\displaystyle\frac{95}{48}$.
Key concepts used: Fraction and percentage concepts.
Problem 10.
In a village each of the 60% of the families has a cow, each of the 30% of the families has a buffalo and each of the 15% of the families has both a cow and a buffalo. If there are 96 families in the village, how many families have neither a cow nor a buffalo?
- 28
- 24
- 20
- 26
Solution 10
Some of families in the group of 30% families each of which has a cow, also has a buffalo. In other words,
60% families each having a cow = families having only a cow + families having both a cow and a buffalo = families having only a cow + 15% of the total number of families
Similarly for families each having a buffalo,
30% families each having a buffalo = families having only a buffalo + families having both a cow and a buffalo = families having only a buffalo + 15% of the total number of families
Summing up these two equations adds the15% twice. Subtracting this 15% from the sum we get,
60% families each having a cow + 30% families each having a buffalo - 15% families having both a cow and a buffalo = families having only a cow + families having only a buffalo + families having both a cow and buffalo,
Or,
75% families = families having only a cow + families having only a buffalo + families having both a cow and a buffalo.
So the percentage of families having neither a cow nor a buffalo = 100% - 75% = 25%.
Total number of families being 96, 25% or one-fourth of which is 24.
Answer: Option b : 24.
Key concepts used: Basic Set union concepts -- Venn diagram concepts.
Explanation of set union with Venn diagram
The following is the diagrammatic representation of various sets of families in the village.
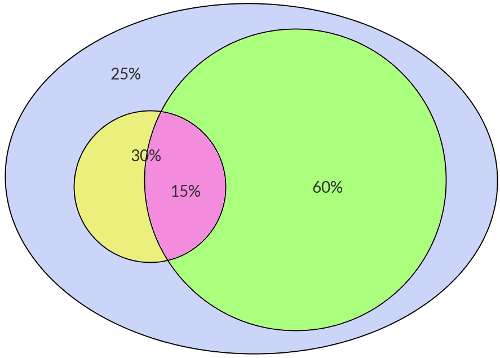
The blue colored whole elliptical region represents the total number of families out of which 60% light green colored region represents families each having a cow and yellow region families each having a buffalo.
But it is not mentioned whether these families of 60% have a buffalo or not. Only when it is mentioned that 15% of families have both a cow and buffalo we immediately understand that this pink colored common region 15% must belong to both the green cow and yellow buffalo regions. In other words, this common region of 15% families is the set intersection of the two sets of cow families and buffalo families.
As this 15% families appear in both 60% and 30%, when we add 60% and 30%, this 15% is included twice. So, 60% + 30% - 15% = 75% gives us the unique families having a cow or a buffalo or both. This is the set union of two sets of cow families and buffalo families.
Thus the rest of the families out of the whole set of families, that is, 100% - 75% = 25% families have neither a cow nor a buffalo.
The above diagram is called as Venn diagram and is used for ease of set representations.
Resources that should be useful for you
7 steps for sure success in SSC CGL tier 1 and tier 2 competitive tests or section on SSC CGL to access all the valuable student resources that we have created specifically for SSC CGL, but generally for any hard MCQ test.
Concept Tutorials on related topics
Basic concepts on fractions and decimals part 1
Basic concepts on Ratio and Proportion
Componendo dividendo applied on number system and ratio proportion problems
How to solve problems on mixing liquids and based on ages
Basic and Rich Percentage Concepts for solving difficult SSC CGL problems
Efficient solution techniques on related topics
How to solve SSC CGL level arithmetic mixture problems in a few simple steps 1
How to solve SSC CGL level arithmetic mixture problems in a few simple steps 2
How to solve SSC CGL level number and age ratio problems lightning fast
How to solve a tricky SSC CGL level age ratio problem lightning fast
SSC CGL level solved question sets on mixture or alligation
SSC CGL level solved questions sets 78 on mixture or alligation 1
SSC CGL level solved question set 85 on mixture or alligation 2
SSC CHSL level solved question sets on Mixture or Alligation
SSC CHSL level Solved Question set 9 on Mixture or Alligation 1
SSC CHSL level Solved Question set 10 on Mixture or Alligation 2
SSC CGL Tier II level solved question sets on mixture or alligation
SSC CGL Tier II level solved question set 24 on mixture or alligation 1
SSC CGL Tier II level solved question set 25 on mixture or alligation 2
SSC CGL Tier II level question and solution sets on Ratio and Proportion
SSC CGL Tier II level Solution Set 23 Ratio proportion 2
SSC CGL Tier II level Question Set 23 Ratio proportion 2
SSC CGL Tier II level Solution Set 22 Ratio proportion 1
SSC CGL Tier II level Question Set 22 Ratio proportion 1
Other SSC CGL question and solution sets on Ratio and Proportion and Percentage
SSC CGL level Solution Set 84, Ratio proportion 8
SSC CGL level Question Set 84, Ratio proportion 8
SSC CGL level Solution Set 83, Ratio Proportion 7
SSC CGL level Question Set 83, Ratio Proportion 7
SSC CGL level Solution Set 76, Percentage 4
SSC CGL level Question Set 76, Percentage 4
SSC CGL level Solution Set 69, Percentage 3
SSC CGL level Question Set 69, Percentage 3
SSC CGL level Solution Set 68, Ratio Proportion 6
SSC CGL level Question Set 68, Ratio Proportion 6
SSC CGL level Solution Set 31, Ratio and Proportion 5
SSC CGL level Question Set 31, Ratio and Proportion 5
SSC CGL Level Solution Set 25, Percentage, Ratio Proportion 4
SSC CGL level Question Set 25, Percentage, Ratio Proportion 4
SSC CGL level Solution Set 24 Arithmetic Ratio Proportion 3
SSC CGL level Question Set 24, Arithmetic Ratio Proportion 3
SSC CGL level Solution Set 5 Arithmetic Ratio Proportion 2
SSC CGL level Question Set 5 Arithmetic Ratio Proportion 2
SSC CGL level Solution Set 4 Arithmetic Ratio Proportion 1
SSC CGL level Question Set 4, Arithmetic Ratio Proportion 1.