
Mensuration for SSC CGL: Quick solutions to 10 questions
Mensuration for SSC CGL Set 86: Know how to visualize 2D and 3D shapes for surface area and volume measurements of 10 questions in 15 minutes.
If you have not taken the test yet, take it first at,
SSC CGL level Question Set 86, Mensuration 6.
Solutions to 10 Mensuration questions for SSC CGL Set 86 - Answering time was 15 mins
Problem 1.
One of the four angles of a rhombus is $60^0$. If the length of each side of the rhombus is 8 cm, then the length of the longer diagonal is,
- $\displaystyle\frac{8}{\sqrt{3}}$ cm
- $8\sqrt{3}$ cm
- $8$ cm
- $4\sqrt{3}$ cm
Solution 1 - Problem analysis and execution
Though the rhombus in the problem can easily be visualized mentally, it is shown in the following figure for easy explanation.

As a rhombus has all four sides of equal length, the side lengths of our rhombus are 8 cm.
The second property of a parallelogram as well as a rhombus is,
Opposite angles are equal.
With one angle given as $60^0$ then, sum of two adjacent angles is $\displaystyle\frac{360^0}{2}=180^0$, and so the other unique angle of the rhombus is,
$180^0-60^0=120^0$.
The third important property of a square and also a rhombus is,
Each diagonal bisects the two corner angles.
The shorter diagonal bisecting the angle $120^0$ to two angles of $60^0$, this shorter diagonal AC effectively bisects the area of the rhombus into two equilateral triangles.
As a result you get the length of shorter diagonal AC as 8 cm.
The fourth and fifth property of a rhombus related to diagonals are,
Diagonals of a rhombus always are perpendicular to each other and also bisect each other.
Finally then you have the two sides of the right $\triangle AED$ as $AE=4$ cm and $AD=8$ cm, which is the hypotenuse.
Use Pythagoras theorem and you get,
$DE=\sqrt{8^2-4^2}=\sqrt{48}=4\sqrt{3}$ cm, and
Longer diagonal, $BD=2AD=8\sqrt{3}$ cm.
Answer: Option b: $8\sqrt{3}$ cm.
Key concepts used: Properties of a rhombus -- Pythagoras theorem.
Problem 2.
Three spherical balls of radii, 2 cm, 4 cm, and 6 cm are melted to form a new spherical ball. In this process, there is a loss of 25% of the material. What is the radius (in cm) of the new ball?
- 6
- 12
- 8
- 16
Solution 2 - Problem analysis and execution
The total volume of the three spherical balls is,
$\frac{4}{3}\pi(2^3+4^3+6^3)=(\frac{4}{3}\pi)(2^3)(1+8+27)$
$=8\times{36}\times{\frac{4}{3}\pi}$.
We have delayed the full calculation of this volume because in the next step we have to calculate the effect of 25% material loss and finally have to again use the volume formula, $\frac{4}{3}\pi r^3$.
25% material loss means final volume will be 75% or $\frac{3}{4}$th of the initial total volume. So the final volume is,
$\frac{3}{4}\times{8}\times{36}\times{\frac{4}{3}\pi}$
$=\frac{4}{3}\pi\times{6^3}=\frac{4}{3}\pi r^3$, where $r$ is the radius of the new sphere.
Radius of the new spherical ball $r$ is then 6 cm.
Answer: Option a : 6.
Key concepts used: Volume of a sphere -- percentage loss concept -- efficient simplification -- Quick calculation -- delayed evaluation technique -- solving in mind.
Quick solution is achieved by delaying the final evaluation. Time and again this strategy resulted in achieving quick solution in mind.
Problem 3.
The curved surface area of a hemisphere is 27.72 sq cm, and volume is 19.404 cubic cm. Find its radius.
- 0.7 cm
- 4.2 cm
- 2.1 cm
- 1.05 cm
Solution 3 - Surface area of a sphere
With radius $r$ of a sphere its surface area is,
$4\pi r^2$.
So curved outer surface area of our hemisphere of radius $r$ is,
$2\pi r^2=27.72$ sq cm.
Solution 3 - Volume of a sphere
Volume of the same sphere of radius $r$ is,
$\frac{4}{3}{\pi}{r^3}=19.404$ cubic cm.
Divide this second equation by the first,
$\frac{1}{3}r=\displaystyle\frac{19.404}{27.72}$ cm,
Or, $r=0.7\times{3}=2.1$ cm.
While dividing as you notice 0.7 to be a candidate quotient, you multiply 27.72 by 0.7 and get exactly 19.404. This is efficient simplification by the use of pattern discovery.
Answer: Option c: 2.1 cm.
Key concepts used: Surface area and volume of a sphere -- Pattern discovery -- Efficient simplification -- Quick calculation -- Solving in mind.
Problem 4.
The radius of cross-section of a solid right circular cylindrical rod is 3.2 dm. The rod is melted and 44 equal solid cubes of side 8 cm are formed. The length of the rod is, (take $\pi=\frac{22}{7}$)
- 56 cm
- 7 cm
- 0.7 cm
- 5.6 cm
Solution 4 - Problem analysis and execution
The volume of 44 equal solid cubes of side 8 cm is,
$44\times{8^3}$ cubic cm.
Volume of the cylindrical rod of length $l$ and radius of cross-section $r=3.2 \text{ dm}=32 \text{ cm}$ is,
$\pi (32)^2l$ cubic cm, converting 1 dm = 10 cm.
Equating the two and simplifying,
$l=44\times{\displaystyle\frac{2^9}{2^{10}}}\times{\displaystyle\frac{7}{22}}$
Or, $l=7$ cm.
To minimize calculation time you didn't evaluate $8^3$ or $32^2$. Rather, knowing that these will be largely cancelled out in the final calculation, you have expressed these two quickly to the common base of 2. This is Efficient simplification or Quick calculation which saves valuable exam hall time.
Answer: Option b: 7 cm.
Key concepts used: Volume of a cube -- Volume of a cylindrical rod -- Alertness to convert decimeter to centimeter -- Efficient simplification -- Quick calculation -- Solving in mind.
Problem 5.
A prism with a right triangular base is 25 cm high. If the shorter sides of the triangle are in the ratio 1 : 2 and volume of the prism is 100 cubic cm, what is the length of the longest side of the triangle?
- $2\sqrt{5}$ cm
- $\sqrt{5}$ cm
- $5$ cm
- $5\sqrt{2}$ cm
Solution 5 - Problem analysis and execution
Naturally you have to be able to visualize or draw the prism in the question for finding the answer quickly. For easy explanation it is shown below.
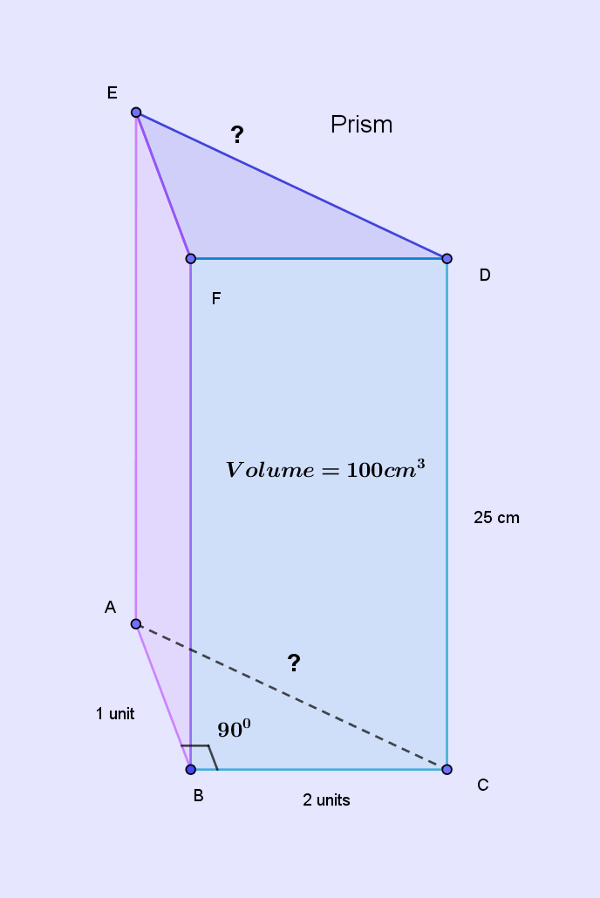
The prism has a triangular base and rises vertically straight to 25 cm height, just like a cylinder. In case of a cylinder, the base is a circle.
The first important property of the prism or a cylinder is,
All horizontal cross-sections parallel to the base will be exactly same as the base.
It means—the volume of the prism will be area of the base times the height—just like the volume of a cylinder.
For our prism volume is 100 cubic cm and height is 25 cm which means the area of the right triangular base will be,
$\displaystyle\frac{100}{25}=4$ sq cm.
The area of the triangle in terms of its shorter sides is,
$\frac{1}{2}\times{2}\times{1}$ square units, as lengths of these two sides are in ratio 2 : 1.
Note: If value of 1 portion of the ratio values be 1 length unit, the lengths of the shorter and the longer sides will respectively be 1 unit and 2 units. We don't yet know the value of 1 length unit.
Equating this with 4 sq cm area you get,
$1 \text{ square unit}=4 \text{ sq cm}$,
Or, $1 \text{ unit}=2\text{ cm}$, be careful—taking the square root of LHS to get 1 unit (not square unit—we have taken the square root to convert 1 square unit to 1 unit) in the LHS doesn't affect value 1, but brings down the RHS value to 2.
This gives us the lengths of the sides as 4 cm and 2 cm.
Apply Pythagoras theorem on the right triangle base to get the length of the longest side hypotenuse as,
$AC=\sqrt{4^2+2^2}=2\sqrt{5}$ cm.
Answer: Option a: $2\sqrt{5}$ cm.
Key concept used: Prism concept -- Prism volume concept -- Ratio concept -- Portions concept -- Pythagoras theorem -- Solving in mind.
Problem 6.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
- 2.25 m
- 4.25 m
- 1.75 m
- 1.125 m
Solution 6 - Problem analysis and execution
You need to just imagine the area of the base of the embankment as difference between the area enclosed by the outer circular edge of the embankment and the area of the circular cross-section of the inner cylindrical well. The schematic is shown below.
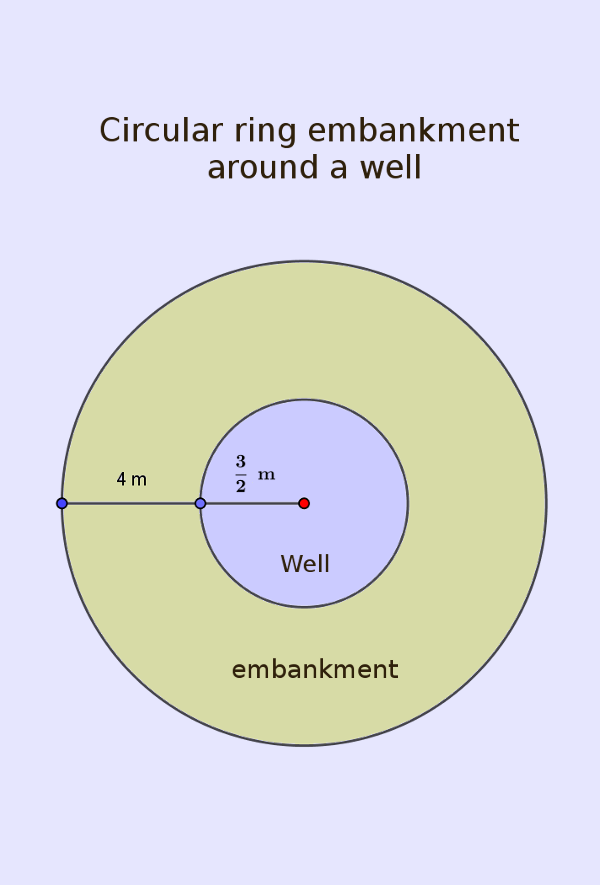
The volume of earth dug is the volume of the well, which is,
$\pi \left(\displaystyle\frac{3}{2}\right)^2\times{14}$ cubic m, be careful to use the radius as $\frac{3}{2}$ m, half of the given value of diameter.
The cross-section area of the ring-shaped embankment is,
$\pi\left[\left(4+\frac{3}{2}\right)^2-\left(\frac{3}{2}\right)^2\right]=28\pi$ sq m, note that $\left(\frac{3}{2}\right)^2$ gets cancelled out.
Dividing the volume of earth dug out by this area of cross-section of the ring embankment, you get the height of embankment as,
$\displaystyle\frac{9}{8}=1.125$ m.
Solution is easy and quick if you take care to convert the diameter of 3 m to radius of $\frac{3}{2}$ m and use the volume of earth in expanded form without calculating its value to divide it finally by the cross-section of the embankment—majority of the elements cancel out reducing calculation load to a minimum. This is achieving efficient simplification by delayed evaluation.
Answer: Option d : 1.125 m.
Key concepts used: Area of a cylinder -- Volume of a cylinder -- Area of a ring -- Volume of a cylindrical ring -- Delayed evaluation -- Efficient simplification -- Quick calculation -- Solving in mind.
Problem 7.
Let ABCDEF be a prism whose base is a right-angled triangle where sides adjacent to $90^0$ are 9 cm and 12 cm. If the cost of painting the prism is Rs. 151.20 at the rate of 20 paise per sq cm, then the height of the prism is,
- 17 cm
- 18 cm
- 16 cm
- 15 cm
Solution 7 - Problem visualization and solution
The problem prism is shown below. It will help visualization and explanation.
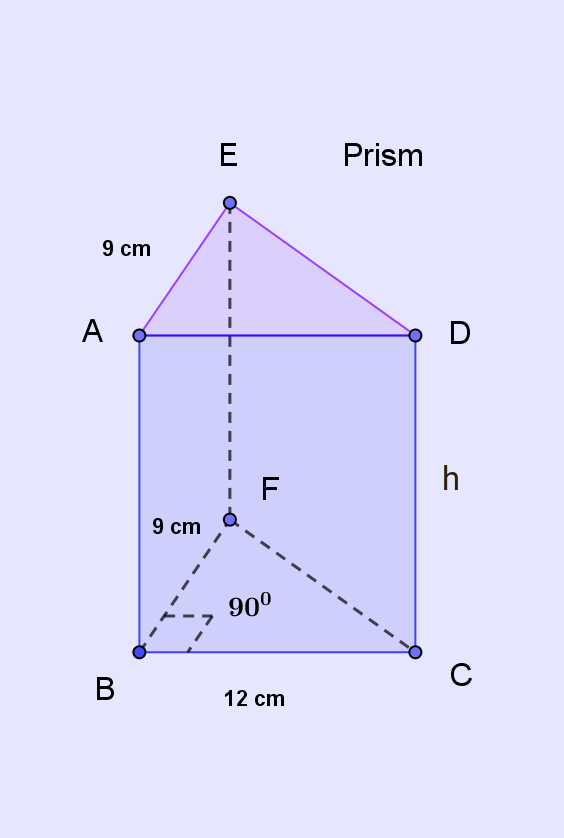
On the right triangle base of $\triangle CBF$ stands the prism vertically upwards $h$ cm tall. You have to find $h$.
Dividing the total expenditure of Rs.151.20 for painting the whole surface area of the prism $Area_{prism}$ at the rate of Rs.0.20 per sq cm, you get this total surface area as,
$Area_{prism}=\displaystyle\frac{151.20}{0.20}=\frac{1512}{2}=756$ sq cm.
Question is: what are the components that make up this surface area of the prism!
The total surface area of the prism is made up of two broad level components—the horizontal surface area of two equal right triangles at base and upper face and the vertical surface area of three vertical rectangular faces—a total of 5 last level area components.
To calculate the area of these components, $\triangle CBF$, $\triangle DEA$ or the vertical surfaces, you need to find first the length of the side $CF$.
And it is easy. Being the hypotenuse of the right $\triangle CBF$, length of $CF$ is,
$CF=\sqrt{CB^2+BF^2}=\sqrt{12^2+9^2}=15$ cm
So, Area of the three vertical faces is,
$Area_{vertical}=h(12+9+15)=36h$.
And twice the area of $\triangle CBF$ is,
$Area_{horizontal}=2\times{\frac{1}{2}}\times{12}\times{9}=108$ sq cm
Total area of the surface area being 756 sq cm, the area of the vertical faces is,
$756-108=648=36h$,
Or, $h=\displaystyle\frac{648}{36}=18$ cm
Answer: Option b: 18 cm.
Key concepts used: Prism surface area -- area of right-angled triangle -- Pythagoras theorem.
Problem 8.
In the given figure, $\triangle ABC$ is drawn such that AB is tangent to a circle at point A. The radius of the circle is 10 cm and BC passes through the center of the circle. Point C lies on the circle. If $BC=36$ cm and $AB=24$ cm, then what is the area of $\triangle ABC$ (in sq cm)?

- 148
- 166.15
- 180
- 168
Solution 8 - Problem analysis and execution
The area of the $\triangle ABC$ is half of its base multiplied by height. In this problem, what will these two be?
Identifying the base and the height of the $\triangle ABC$ are the main tasks that will solve the problem instantly.
Here you need a little visualization to imagine the height to be a perpendicular dropped from C to a point E on BA extended. As radius OA is also perpendicular to BA at point A (because BA being tangent to the circle at A, radius OA is perpendicular to BA), it will be parallel to CE and the two triangles $\triangle BAO$ and $\triangle BEC$ will be similar with equal ratio of corresponding sides.
This is the quickest and easiest way to get the height of the $\triangle ABC$, which is EC. We already know the base as 24 cm.
Let us first redraw the problem figure with the perpendicular CE as the new element introduced. The figure is shown below.
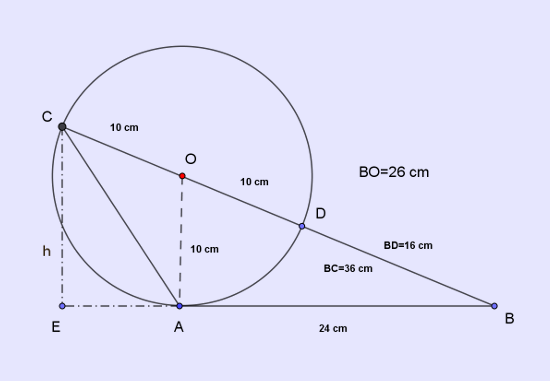
In two triangles, $\triangle BAO$ and $\triangle BEC$, bases AO and EC are parallel to each other and so, the two triangles are similar to each other (all three corresponding pairs of angles equal).
By the property of two similar triangles, you would have ratios of three pairs of corresponding sides in the two similar triangles equal to each other. More specifically, numerator sides taken from the larger $\triangle BEC$ you form the equality relations as,
$\displaystyle\frac{EC}{AO}=\frac{BC}{BO}=\frac{BE}{BA}$.
You won't need the third ratio for solving the problem.
Considering just the equality of the first two ratios, you would get,
$\displaystyle\frac{EC}{AO}=\frac{36}{26}$
Or, height $h=EC=\displaystyle\frac{360}{26}$, as AO=10, BC=36 and BO=26.
Now you know the height of $\triangle ABC$, and also its base value of $AB=24$ cm.
Area of the $\triangle ABC$ is,
$Area=\frac{1}{2}\times{24}\times{\displaystyle\frac{360}{26}}$
$=12\times{\displaystyle\frac{180}{13}}=\displaystyle\frac{2160}{13}=166.15$ sq cm.
Answer: Option b: 166.15.
Key concepts used: Properties of a tangent to a circle -- Conditions of two similar triangles -- Corresponding sides equality property of two similar triangles -- Area of a triangle formula.
How to identify the corresponding pair of sides in two similar triangles is explained in the following section. If you are already aware of this, skip the section.
How to identify the corresponding pairs of sides in two similar triangles
The ratios of pairs of corresponding sides of two similar triangles are equal to each other.
Question is which are the three pairs of corresponding sides? What are the rules of pairing two sides from two similar triangles and forming the three equal ratios?
The rules are simple,
In forming the three ratios, first select the triangle from which you will pick up the numerator sides. In our case, we have selected the sides from the larger $\triangle BEC$.
Select as numerator any side of the first triangle (larger triangle in our case) and choose the angle to which the side is opposite. Select from the second triangle the denominator as—the side that is opposite to the angle in the second triangle equal to the angle chosen in the first triangle.
In short,
The corresponding sides in equal ratios are the sides opposite to equal angles in two similar triangles.
For example, in our case, for the first ratio, $\displaystyle\frac{EC}{AO}$, EC and AO are both opposite to the common angle $\angle EBC=\angle ABO$, and for the second ratio, $\displaystyle\frac{BC}{BO}$, BC and BO are both opposite to the equal angles of $90^0$.
Problem 9.
Two smaller circles touch a larger circle internally and pass through the center $O$ of the larger circle. If the diameter of the larger circle is 28 cm, what is the area of the larger circle which is not enclosed by the smaller circles?
- 256 sq cm
- 308 sq cm
- 154 sq cm
- 616 sq cm
Solution 9 - Problem analysis and execution
The figure representing the problem that you would have to use is shown below,

The diameter AB of the larger circle is 28 cm. It encloses the two smaller circles each passing though its center touching it internally. This is the only possible configuration for the problem and you have to evaluate the yellow shaded area which is area of larger circle minus areas of two smaller circles.
Once you draw the figure, rest is easy. The required area is,
$\pi (14)^2-2\pi(7^2)=2\times{\displaystyle\frac{22}{7}}\times{7^2}=308$ sq cm.
Easy to solve mentally.
Answer: Option b: 308 sq cm.
Key concepts used: Area of circle -- visualization -- internally touching pair of circles.
Problem 10.
In the given figure, PB is one-third of AB and BQ is one-third of BC. If the area of BPDQ is 20 sq cm, then what is the area (in sq cm) of ABCD?

- 60
- 30
- 40
- 45
Solution 10 - Problem analysis and quick solution using basic concepts on area of a rectangle and a triangle
We'll use the given figure in the question for explaining the solution.
DP and DQ have segmented the total area of the rectangle into three parts one of which BPDQ is of area 20 sq cm.
Our broad strategy for solving the problem will be as follows.
The other two parts are two triangles, $\triangle PAD$ and $\triangle QDC$. We'll find the area of these two triangles in terms of the two sides of the rectangle ABCD, subtract the total area of the two triangles from the total area of the rectangle and equate the result with 20 sq cm.
This will give us the value of the product of the two sides of the rectangle and so its area.
BP is one-third of AB. So, AP is two-third of AB and the area of the $\triangle APD$ is,
$A_{APD}=\frac{1}{2}AD\times{\frac{2}{3}AB}=\frac{1}{3}(AB\times{AD})$.
Similarly, as BQ is one-third of BC, QC is two-third of BC and the area of $\triangle QDC$ is,
$A_{QDC}=\frac{1}{2}DC\times{\frac{2}{3}BC}=\frac{1}{3}(AB\times{AD})$.
So the area of the two triangles are equal and each is one-third of the area of the rectangle $AB\times{AD}$.
The rest of the area of the rectangle which is area 20 sq cm of BPDQ is also then one-third of the area of the rectangle.
The area of the rectangle is, 60 sq cm.
Answer: a: 60.
Key concepts used: Deductive reasoning -- Key pattern discovery -- Strategic problem solving -- Area of triangle -- Area of rectangle -- Solving in mind.
Other related question set and solution set on SSC CGL mensuration
SSC CGL level Solution Set 88 on Mensuration 8
SSC CGL level Question Set 88 on Mensuration 8
SSC CGL level Solution Set 87 on Mensuration 7
SSC CGL level Question Set 87 on Mensuration 7
SSC CGL level Solution Set 86 on Mensuration 6
SSC CGL level Question Set 86 on Mensuration 6
SSC CGL level Solution Set 43 on Mensuration 5
SSC CGL level Question Set 43 on Mensuration 5
SSC CGL level Solution Set 42 on Mensuration 4
SSC CGL level Question Set 42 on Mensuration 4
SSC CGL level Solution Set 41 on Mensuration 3
SSC CGL level Question Set 41 on Mensuration 3
SSC CGL level Solution Set 27 on Mensuration 2
SSC CGL level Question Set 27 on Mensuration 2
SSC CGL level Solution Set 26 on Mensuration 1
SSC CGL level Question Set 26 on Mensuration 1