
Mensuration for SSC CGL: Quick solutions to 10 questions
Mensuration for SSC CGL Set 87: Learn how to imagine 2D and 3D shapes for surface area and volume measurements of 10 questions in 15 minutes.
If you have not taken the test yet, take it first at,
SSC CGL level Question Set 87, Mensuration 7.
Solutions to 10 Mensuration questions for SSC CGL Set 87 - Answering time was 15 mins
Problem 1.
In the figure below O is the center of the circle and $\angle AOB=150^0$. If the shaded portion is $x$ part of the circular region, then value of $x$ is,
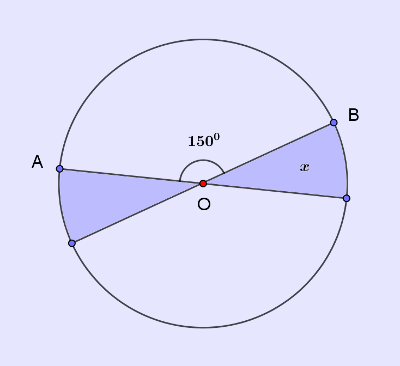
- $\displaystyle\frac{1}{12}$
- $\displaystyle\frac{1}{9}$
- $\displaystyle\frac{1}{4}$
- $\displaystyle\frac{1}{6}$
Solution 1 - Problem analysis and execution
We'll use the following figure for explaining the solution.

The fundamental relation between the length of an arc, angle held by it at the center and area enclosed by the arc at the center of a circle is,
Arc length as well as the angle it holds at the center are directly proportional to the area the arc encloses at the center of the circle.
The whole circle is the perimeter length of $2\pi r$, where $r$ is the radius of the circle. And the angle held by this circumference at the center of the circle is $360^0$. This circumference covers the whole area of the circle $\pi r^2$.
The angle held by the arc BD in our circle is $30^0$ which is $\frac{1}{12}$th of $360^0$. So area BOD the arc BD will enclose at the center is $\frac{1}{12}$th of the area of the circle.
But the shaded area is twice this area. So the shaded area must be $\frac{1}{6}$th of the area of the circle.
In other words,
$x=\displaystyle\frac{1}{6}$.
Answer: Option d: $\displaystyle\frac{1}{6}$.
Key concepts used: Proportionality Relation between angle held by an arc at the center and the area enclosed by the same arc at the center -- Arc area relation -- Solving in mind.
Problem 2.
If $D$, $E$, and $F$ are the mid-points of the sides of an equilateral $\triangle ABC$, then the ratio of the area of the $\triangle DEF$ and $\triangle DCF$ is,

- $1.1:1$
- $1:1$
- $1:1.1$
- $0.9:1$
Solution 2 - Problem analysis and execution
From the figure it looks like CDEF is a rhombus, the two triangles $\triangle DEF$ and $\triangle DCF$ are congruent and answer should be 1 : 1. But we have to be sure about that.
Let us see how quickly we can be sure about our hypothesis.
DE joining the mid-points of BC and AB, it is parallel to AC, $\triangle BED$ and $\triangle BAC$ are similar and $DE=\frac{1}{2}\text{ of }AC=CF$. By the same logic, $EF=DC$ and side DF is common between the two triangles $\triangle DEF$ and $\triangle DCF$.
With three sides equal to each other, the two triangles are congruent with equal areas.
The ratio of their areas is then 1 : 1.
Answer: Option b : 1 : 1.
Key concepts used: Properties of an equilateral triangle -- Triangle similarity condition -- Equal ratio of corresponding sides of two triangles -- Congruency of two triangles -- solving in mind.
In fact the two triangles are also equilateral, but that is not our job to prove.
Problem 3.
The centroid of a $\triangle ABC$ is $G$. If the area of the $\triangle ABC=72$ sq units, the area of $\triangle BGC$ is,
- 36 sq units
- 48 sq units
- 16 sq units
- 24 sq units
Solution 3 - Problem solving using median segmentation ratio at centroid and similar triangle concepts
The figure we'll use for explaining the solution is shown below.

First we'll use the concept of segmentation of median AD of a triangle at its centroid G in the ratio of 2 : 1 with longer segment GA towards the vertex A.
So in our problem,
$AG: GD=2:1$,
Or, $GD : AD= 1: 3$.
As the area of the $\triangle ABC=72$ sq units, and you have to find the shaded area of the $\triangle BGC$, you'll drop two perpendiculars GP from the centroid to BC and AQ from vertex A to BC.
GP is the height of the $\triangle BGC$ with base as BC, and AQ is the height of the $\triangle ABC$ with same base BC.
The area of the $\triangle BGC$ is then,
$A_{BGC}=\frac{1}{2}BC\times{GP}$,
And area of $\triangle ABC$ is,
$A_{ABC}=\frac{1}{2}BC\times{AQ}$.
Ratio of the two is,
$\displaystyle\frac{A_{BGC}}{A_{ABC}}=\frac{GP}{AQ}$,
Or, $A_{BGC}=72\times{\displaystyle\frac{GP}{AQ}}$.
If you find the value of this ratio you'll get the desired area.
Second stage: Using similar triangles concept
Now you'll explore the relation between the two right triangles $\triangle AQD$ and $\triangle GPD$.
Consider GP and AQ as two bases of these two triangles and these are parallel to each other. So these two triangles are similar.
By the equal corresponding side ratio property of two similar triangles you'll have now,
$\displaystyle\frac{GP}{AQ}=\frac{GD}{AD}=\frac{1}{3}$, by the property of median section ratio at centroid.
You have used two properties one after the other.
Rule of forming the equal ratios of corresponding sides in two similar triangles
How did you identify GP and AQ as corresponding sides? Simple. Both of these are opposite to the same common $\angle GDP=\angle ADQ$. Same way GD and AD are corresponding sides of the two triangles as both of these are opposite to the right angle in the two triangles. You have chosen the side from the smaller triangle first for the numerator in both the ratios.
Key technique is to choose the two sides opposite to two equal angles from the two triangles.
So, $A_{BGC}=72\times{\displaystyle\frac{GP}{AQ}}=72\times{\frac{1}{3}}=24$ sq units.
Answer: Option d: 24 sq units.
Key concepts used: Median section ratio at centroid -- Area of a triangle as half of base multiplied by height -- Similar triangles condition -- Equal corresponding side ratio property of similar triangles -- Solving in mind.
Problem 4.
In a trapezium $ABCD$, $AD || BC$, $AD \lt BC$, $BC = 6$ cm and distance between parallel sides is 4 cm. If the area of $ABCD$ is 16 sq cm, then length of $AD$ is,
- 2 cm
- 3 cm
- 1 cm
- 8 cm
Solution 4 - Problem analysis and execution
Let us first solve the problem mentally without drawing the diagram.
First assumption: Imagine one vertical side is perpendicular to both horizontal parallel sides.
Extend the smaller side to meet the other perpendicular dropped from the other end of the longer side to form a rectangle of area,
$6\times{4}=24$ sq cm.
The difference of larger and smaller side lengths forms the base of a right triangle with vertex at the other end of the longer side. This triangle area is the difference in area of the rectangle and the trapezium, which is, $24-16=8$ sq cm.
The height of this right triangle is 4 cm and so base must be 4 cm for its area to be 8 sq cm. This being the difference in lengths between the shorter and the longer parallel sides of the trapezium, the length of the shorter side of the trapezium must be,
$6-4=2$ cm.
Our first assumption can always be made as the area of the trapezium does not change if you slide the shorter side horizontally keeping the vertical distance from the longer parallel side fixed.
This way of thinking makes your ability to visualize and solve this type of graphical problems faster.
Let us now explain using the following diagram.

AD and BC are the two parallel sides of trapezium ABCD. Vertical distance between the two sides is AB = 4 cm.
As imagined, AD is extended to E to form a rectangle ABCE of area,
$6\times{4}=24$ sq cm.
The difference of $8$ sq cm between this rectangle area and the trapezium area of 16 cm must be the area of the $\triangle CDE$.
Base of this triangle is DE and height is $CE=BA=4$ cm.
So, $8 = \frac{1}{2}DE\times{4}=2DE$,
Or, $DE=4$ cm, and shorter side length,
$AD=6-4=2$ cm.
This follows our reasoning without drawing the diagram.
If you slide the side AD along AE to say, A'D' horizontally keeping base BC fixed, the area of the trapezium doesn't change. That's the reason behind our convenient assumption of the configuration of the trapezium with height AB as one vertical side. This is also called translation of the side AD along AE horizontally.
You can always make this assumption in this type of problem.
Answer: Option a: 2 cm.
Key concepts used: Trapezium concepts -- Translation of a parallel side -- Trapezium area as the difference between area of a rectangle and a triangle -- Area of a triangle -- Visualization -- Solving in mind.
Problem 5.
Two identical circles intersect so that their centers and points at which they intersect form a square of side 2 cm. What is the area (in sq cm) of the portion that is common to the two circles?
- $3\pi-4$
- $\pi-2$
- $4\pi-8$
- $2\pi-4$
Solution 5 - Problem analysis and execution
For easy explanation the representative figure is shown below.
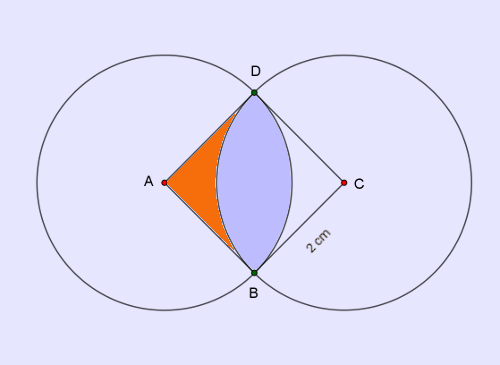
ABCD is the square of side length 2 cm. A and C are the centers of the two identical circles and B and D are their points of intersection.
Your job is to find the area of the portion that is common to the two circles—it is the blue shaded area.
You reason from the figure that the easiest way to find this target area would be to subtract from the area held by the arc BD at the center (of corresponding circle), the area of orange shaded sliver of the area.
Area enclosed by the arc BD is known—it is $\frac{1}{4}$th of the area of any of the identical circles as the arc holds an angle of $90^0$ at the center (as ABCD is a square, all its internal angles are $90^0$, $\angle DAB=90^0$).
Again, the radius of any of the circles being 2 cm (side length of the square), its area is,
$4\pi$ sq cm.
So the area enclosed by the arc BD is just $\pi$ sq cm.
Subtract this from the area of the square—4 sq cm and you will get, $(4-\pi)$ sq cm as the area of the orange shaded sliver of the region.
Now subtract this area of $(4-\pi)$ sq cm from $\pi$ sq cm and you will get the target area as,
$\pi-(4-\pi)=2\pi -4$ sq cm.
Answer: Option d: $2\pi-4$.
Key concept used: Two intersecting circles -- Angle held by an arc at the center of a circle -- Area enclosed by an arc at the center -- Arc angle to arc area proportionality -- Properties of a square -- Solving in mind.
Problem 6.
A solid right circular cylinder and a solid hemisphere stand on equal bases and have the same height. The ratio of their whole surface area is,
- 3 : 2
- 2 : 3
- 4 : 3
- 3 : 4
Solution 6 - Problem analysis and execution
The two bases are circular with same radius as say, $r$.
As the height of the hemisphere also equals radius of its base, the height of the cylinder is same as the radius of its base.
These two steps are fact finding. Now we can get down to the task of finding the two surface areas.
The whole surface area of the hemisphere consists of the area of its curved face which is half the surface area of the sphere $4\pi r^2$ plus area of its circular base. It is then,
$A_{hemisphere}=2\pi r^2+\pi r^2=3\pi r^2$.
And the whole surface area of the cylinder consists of area of its two horizontal faces plus the area of its vertical curved face. It is then,
$A_{cylinder}=2\pi r^2+2\pi r\times{r}=4\pi r^2$.
So, $\displaystyle\frac{A_{cylinder}}{A_{hemisphere}}=4: 3$.
Answer: Option c : 4 : 3.
Key concepts used: Hemisphere concepts -- Whole Surface area of a cylinder -- Surface area of a sphere -- Ratio concept -- Solving in mind.
Problem 7.
Three medians AD, BE and CF of $\triangle ABC$ intersect at G. The area of $\triangle ABC$ is 36 sq cm. Then the area of $\triangle CGE$ is,
- 12 sq cm
- 6 sq cm
- 18 sq cm
- 9 sq cm
Solution 7 - Problem visualization and solution
The problem triangle is shown below. It will help visualization and explanation.

AD, BE and CF are the three medians intersecting at centroid G.
The centroid segments each of the medians into two segments in a 2 : 1 ratio with larger segment towards the vertex.
For example, BG is 2 units, and GE is 1 unit long.
Given is the area of the $\triangle ABC$ as 36 sq cm.
As each median also divides the area of the triangle into two equal portions, area of the $\triangle BCE=\frac{1}{2}\times{36}=18$ sq cm. This area equals product of half of base CE and height BQ,
$A_{BCE}=18=\frac{1}{2}\times{CE}\times{BQ}$.
The $\triangle CGE$ stands on the same base CE and its area is the product of half of CE and height GP,
$A_{CGE}=\frac{1}{2}\times{CE}\times{GP}$.
Take the ratio of the two areas and you get,
$\displaystyle\frac{A_{CGE}}{A_{BCE}}=\frac{GP}{BQ}$.
We are very near to the solution now.
In this second stage we just have to find the value of the ratio of heights of the two triangles $\displaystyle\frac{GP}{BQ}$.
Second stage solution: Concept used: Corresponding pair of sides are in equal ratio in two similar triangles
The two triangles $\triangle BQE$ and $\triangle GPE$ are similar with bases BQ parallel to GP (as both are perpendicular to AC). The ratio of pairs of corresponding sides in the two triangles are equal.
We'll use specifically,
$\displaystyle\frac{GP}{BQ}=\frac{GE}{BE}$.
As centroid segments BE at G in a ratio of 2 : 1, BE is 3 units and GE is 1 unit.
So, $\displaystyle\frac{GE}{BE}=\frac{1}{3}$, and area of $\triangle CGE$ is,
$A_{CGE}=18\times{\frac{1}{3}}=6$ sq cm.
Answer: Option b: 6 sq cm.
Key concepts used: A Median divides area of triangle into two equal parts -- Conditions of similar triangles -- Side ratio equality in similar triangles -- Median section ratio at centroid -- Area of triangle as half of base multiplied by its height -- Solving in mind.
Yes, you can easily solve the problem in mind using the concepts in two stages and visualization of the figure.
Problem 8.
The surface area of one cone is twice that of the second cone and the slant height of the latter is twice that of former. The ratio of their radii is,
- 1 : 4
- 4 : 3
- 3 : 4
- 4 : 1
Solution 8 - Problem analysis and execution
Assume $r_1$, $r_2$ and $l_1$, $l_2$ to be the radii and slant heights of the first and second cone respectively.
By the first statement,
$\pi r_1l_1=2\pi r_2l_2=4\pi r_2 l_1$, as slant height of the second cone is twice that of first cone by the second statement.
So, $r_1 : r_2=4 : 1$.
Answer: Option d: 4 : 1.
Key concepts used: Surface area of a cone is $\pi r l$ where $r$ is the base radius and $l$ is the slant height of the cone -- Ratio concept -- Solving in mind.
Problem 9.
The diameter of a sphere is twice the diameter of another sphere. The curved surface area of the first and the volume of the second are numerically equal. The numerical value of the radius of the first sphere is,
- 8
- 24
- 16
- 3
Solution 9 - Problem analysis and execution
Let's assume $r_1$ and $r_2$ to be the radii of the two spheres.
By the first statement then,
$r_1=2r_2$.
Curved surface area of the first sphere is,
$4\pi r_1^2$.
Volume of the second sphere is,
$\frac{4}{3}\pi r_2^3=\frac{1}{6}\pi r_1^3$, as $r_2^3=\frac{1}{8}r_1^3$.
By the second statement the surface area of the first is numerically equal to the volume of the second. So,
$4\pi r_1^2=\frac{1}{6}\pi r_1^3$,
Or, $r_1=24$.
Answer: Option b: 24.
Key concepts used: Curved surface area of a sphere -- Volume of a sphere -- Solving in mind.
Problem 10.
A rectangular paper sheet of dimensions 22 cm x 12 cm is folded in the form of a cylinder along its length. What will be the volume enclosed by the cylinder? (Take $\pi=\frac{22}{7}$)
- $624\text{ cm}^3$
- $400\text{ cm}^3$
- $462\text{ cm}^3$
- $460\text{ cm}^3$
Solution 10 - Problem analysis and quick solution by problem definition and cylinder volume concepts
The key to solving this problem in mind is to visualize and define the cylinder precisely as its height as width 12 cm of the paper and perimeter $2\pi r$ of the cylinder as the length 22 cm of the paper, $r$ being the radius of the base of the cylinder.
This is because the paper has been folded along its length.
With $2 \pi r=22$,
$r=\displaystyle\frac{7}{2}$.
With height of the cylinder as $h=12$ cm, its volume will then be,
$V_{cylinder}=\pi r^2 h=\displaystyle\frac{22\times{7}\times{12}}{4}=7\times{66}=462$.
The figure of the cylinder is shown below.

Answer: c: $462\text{ cm}^3$.
Key concepts used: Visualization -- Paper folding to form a cylinder -- Precise problem definition -- Cylinder base perimeter -- Cylinder volume -- Delayed evaluation -- Solving in mind.
Other related question set and solution set on SSC CGL mensuration
SSC CGL level Solution Set 88 on Mensuration 8
SSC CGL level Question Set 88 on Mensuration 8
SSC CGL level Solution Set 87 on Mensuration 7
SSC CGL level Question Set 87 on Mensuration 7
SSC CGL level Solution Set 86 on Mensuration 6
SSC CGL level Question Set 86 on Mensuration 6
SSC CGL level Solution Set 43 on Mensuration 5
SSC CGL level Question Set 43 on Mensuration 5
SSC CGL level Solution Set 42 on Mensuration 4
SSC CGL level Question Set 42 on Mensuration 4
SSC CGL level Solution Set 41 on Mensuration 3
SSC CGL level Question Set 41 on Mensuration 3
SSC CGL level Solution Set 27 on Mensuration 2
SSC CGL level Question Set 27 on Mensuration 2
SSC CGL level Solution Set 26 on Mensuration 1
SSC CGL level Question Set 26 on Mensuration 1