
Algebra for SSC CGL: Questions Answers Solutions Set 98
Solve 10 questions on algebra for SSC CGL Set 98 in 15 mins. Verify from answers and finally learn how to solve quickly the right way from the solutions.
A few of these 10 are hard algebra questions that are solved quickly by advanced problem solving techniques.
This set contains,
- Selected questions on Algebra for SSC CGL to be answered in 15 minutes (10 chosen questions)
- Answers to the questions, and
- Quick solutions to the questions.
Special attention is given for quick solution of all the questions. Use the question set for timed mock test and clarify the doubts from the solutions for getting best results.
10 Questions on Algebra for SSC CGL Set 98 - answering time 15 mins
Q1. If $(8x^3-27y^3) \div (2x-3y)=(Ax^2+Bxy+Cy^2)$ then the value of $(2A+B-C)$ is,
- $3$
- $4$
- $5$
- $6$
Q2. If $4x+5y=83$ and $3x:2y=21:22$, then $(y-x)$ equals
- $3$
- $4$
- $7$
- $11$
Q3. If $(x+4)^3+(2x+1)^3+(2x+5)^3=(3x+12)(2x+1)(2x+5)$, then what is the value of $x$?
- $-2$
- $-3$
- $3$
- $2$
Q4. The graph of the linear equation $3x+4y=24$ is a straight line intersecting $x$-axis and $y$-axis at the points $A$ and $B$ respectively. $\text{P(2, 0)}$ and $\text{Q(0, }\frac{3}{2}\text{)}$ are two points on sides $OA$ and $OB$ respectively of $\triangle OAB$ where $O$ is the origin of the Coordinate system. Given that $AB=10$ cm, then value of $PQ$ is,
- $5$ cm
- $20$ cm
- $40$ cm
- $2.5$ cm
Q5. If $ab+bc+ca=8$, and $a^2+b^2+c^2=20$, then a possible value of $\frac{1}{2}(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]$ is,
- $80$
- $84$
- $72$
- $56$
Q6. If $a+b+c=m$, and $\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}+\displaystyle\frac{1}{c}=0$, then average of $a^2$, $b^2$ and $c^2$ is,
- $\displaystyle\frac{m^2}{3}$
- $\displaystyle\frac{m^2}{9}$
- $m^2$
- $\displaystyle\frac{m^2}{27}$
Q7. If $a+b+c=9$, $ab+bc+ca=26$, $a^3+b^3=91$, $b^3+c^3=72$ and $c^3+a^3=35$, then what is the value of $abc$?
- $42$
- $24$
- $36$
- $48$
Q8. If $x=\sqrt[3]{x^2+11}-2$, then the value of $(x^3+5x^2+12x)$ is,
- $0$
- $11$
- $7$
- $3$
Q9. If $a^3+3a^2+9a=1$, then what is the value of $a^3+\displaystyle\frac{3}{a}$?
- $31$
- $24$
- $26$
- $28$
Q10. If $x+3y-\displaystyle\frac{2z}{4}=6$, $x+\frac{2}{3}(2y+3z)=33$ and $\frac{1}{7}(x+y+z)+2z=9$, then what is the value of $46x+131y$?
- $414$
- $464$
- $364$
- $384$
Answers to the questions on algebra for SSC CGL Set 98
Q1. Answer: Option c: $5$.
Q2. Answer: Option b: $4$.
Q3. Answer: Option a: $-2$.
Q4. Answer: Option d: $2.5$ cm.
Q5. Answer: Option c: $72$.
Q6. Answer: Option a: $\displaystyle\frac{m^2}{3}$.
Q7. Answer: Option b: $24$.
Q8. Answer: Option d: $3$
Q9. Answer: Option d: $28$.
Q10. Answer: Option a: $414$.
Solutions to the questions on algebra for SSC CGL Set 98 - answering time was 15 mins
Q1. If $(8x^3-27y^3) \div (2x-3y)=(Ax^2+Bxy+Cy^2)$ then the value of $(2A+B-C)$ is,
- $3$
- $4$
- $5$
- $6$
Solution 1: Quick solution by two-factor expansion of sum of cubes and comparison of coefficients of like terms
As the first factor in LHS is expanded in its two-factor form, $(2x-3y)$ in the divisor cancels out with one of the two factors of $(8x^3-27y^3)$,
$E=\displaystyle\frac{(8x^3-27y^3)}{(2x-3y)}=\frac{(2x)^3-(3y)^3}{(2x)-(3y)}$
$=\displaystyle\frac{(2x-3y)[(2x)^2+(3y)^2+6xy]}{(2x-3y)}$
$=4x^2+6xy+9y^2$.
The two-factor expanded form of subtractive sum of cubes is used with abstracted compound variables $a=2x$ and $b=3y$,
$a^3-b^3=(a-b)(a^2+b^2+ab)$.
Now equating simplified result with the given RHS,
$4x^2+6xy+9y^2=Ax^2+Bxy+Cy^2$.
Comparing the coefficients of like terms, $x^2$, $xy$ and $y^2$ on both sides of the equation,
$A=4$, $B=6$ and $C=9$.
And the target expression value is,
$(2A+B-C)=8+6-9=5$.
Answer: Option c: $5$.
Key concepts used: Key pattern identification -- Simplification by expanding sum of cubes to its two-factor expanded form -- Comparison of coefficients of like terms -- Solving in mind.
With concepts and calculations simple, the question can easily be solved in mind.
Q2. If $4x+5y=83$ and $3x:2y=21:22$, then $(y-x)$ equals
- $3$
- $4$
- $7$
- $11$
Solution 2: Quick solution by substituting value of $\displaystyle\frac{x}{y}$ from the proportion to the given equation bypassing solving a pair of linear equations
Solve quickly by first getting value of $\displaystyle\frac{x}{y}$ from the given proportion,
$\displaystyle\frac{x}{y}=\frac{7}{11}$,
And then substituting this value in the transformed given linear equation,
$4\displaystyle\frac{x}{y}+5=\displaystyle\frac{83}{y}$,
Or, $\displaystyle\frac{28}{11}+5=\displaystyle\frac{83}{y}$,
Or, $\displaystyle\frac{83}{11}=\frac{83}{y}$.
So, $y=11$ and from $\displaystyle\frac{x}{y}=\frac{7}{11}$,
$x=7$, and,
$(y-x)=4$.
Quick solution with minimum calculation.
Answer: Option b: $4$.
Key concepts used: Avoiding solution of a pair of linear equations by substituting value of compound variable $\displaystyle\frac{x}{y}$ from the given proportion to the suitably transformed linear equation -- Solving in mind.
Q3. If $(x+4)^3+(2x+1)^3+(2x+5)^3=(3x+12)(2x+1)(2x+5)$, then what is the value of $x$?
- $-2$
- $-3$
- $3$
- $2$
Solution 3: Quick solution by identification of key pattern of sum of cubes of three compound variables equal to three times their product and applying three variable zero sum principle
Identify the key pattern that the given equation can be simplified as a sum of cubes of three compound variables equaling three times their product,
$(x+4)^3+(2x+1)^3+(2x+5)^3=(3x+12)(2x+1)(2x+5)$
$=3(x+4)(2x+1)(2x+5)$
Or, $p^3+q^3+r^3=3pqr$, ..............................(1)
Where the three compound variables are represented by the dummy variables,
$(x+4)=p$,
$(2x+1)=q$, and,
$(2x+5)=r$.
Equation (1) satisfying the three variable zero sum principle in reverse form, sum of the three variables $p$, $q$ and $r$ is zero,
$p+q+r=(x+4)+(2x+1)+(2x+5)=0$,
Or, $5x=-10$,
Or, $x=-2$.
Answer: Option a: $-2$.
Key concepts used: Key pattern identification -- Abstraction of compound variables by dummy variable substitution and resulting simplification -- Three variable zero sum principle in reverse form -- Solving in mind.
Reverse form of three variable zero sum principle
Usually we know three variable zero sum principle as the result of,
If sum of three variables, $a+b+c=0$, sum of their cubes will be equal to three times the product of the variables,
$a^3+b^3+c^3=3abc$.
For this powerful principle derived from mathematical deduction, the reverse also holds true. That is,
If sum of cubes of three variables equals three times their product, sum of the three variables will be zero. Mathematically,
If $a^3+b^3+c^3=3abc$, $a+b+c=0$.
Let's deduce both of these results from the two-factor expansion of three variable sum of cubes,
$a^3+b^3+c^3=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)+3abc$.
You may verify this algebraic identity by expanding the product on the RHS. All the terms will cancel out leaving only $a^3+b^3+c^3$.
In the two-factor expansion of the three variable sum of cubes, if $(a+b+c)=0$, RHS turns to $3abc$ satisfying the usual form of the three variable zero sum principle.
Alternately, if $a^3+b^3+c^3=3abc$,
$(a+b+c)(a^2+b^2+c^2-ab-bc-ca)=0$,
Or, $a+b+c=0$.
$(a^2+b^2+c^2-ab-bc-ca)=0$ occurs only when $a=b=c$ which we ignore as a trivial case.
Q4. The graph of the linear equation $3x+4y=24$ is a straight line intersecting $x$-axis and $y$-axis at the points $A$ and $B$ respectively. $\text{P(2, 0)}$ and $\text{Q(0, }\frac{3}{2}\text{)}$ are two points on sides $OA$ and $OB$ respectively of $\triangle OAB$ where $O$ is the origin of the Coordinate system. Given that $AB=10$ cm, then value of $PQ$ is,
- $5$ cm
- $20$ cm
- $40$ cm
- $2.5$ cm
Solution 4: Quick solution by Graphical representation of a straight line plotted on a two-axis coordinate system, Similarity of triangle
This is a problem of graphical algebra problem solving on a two-axis $x$-$y$ coordinate system.
It is easy to draw the approximate sketch in a few seconds and solve the problem in maximum 30 seconds but we would solve it in mind just by step by step reasoning based on the concepts of simple geometry and coordinate system.
First find the coordinates of $A$ and $B$.
Co-ordinates of $A$ on $x$-axis: With $y=0$ in $3x+4y=24$, $x=8$: Coordinates $\text{A(8, }0\text{)}$.
Co-ordinates of $B$ on $y$-axis: With $x=0$ in $3x+4y=24$, $y=6$: Coordinates $\text{B(0, }6\text{)}$.
Line $AB$ joins $\text{A(8, }0\text{)}$ and $\text{B(0, }6\text{)}$ and is of length $10$ cm.
Conclusion 1:$AB$ is the hypotenuse of the right-angled triangle $\triangle OAB$ where $O$ is the origin, $OA=8$ cm is the base and $OB=6$ cm is the height.
What about the points $\text{P(2, 0)}$ on $x$-axis and $\text{Q(0, }\frac{3}{2}\text{)}$ on $y$-axis?
Identify the pattern that $OP=2\text{ cm}=\frac{1}{4}\text{th of Base }OA$, and,
$OQ=\frac{3}{2}\text{ cm}=\frac{1}{4}\text{th of Height }OB$.
$\triangle OPQ$ also is a right-angled triangle with right-angle at $O$ common to $\triangle OAB$.
Relating triangles $\triangle OPQ$ and $\triangle OAB$ for finding a relation between $PQ$ and $AB$
The ratio of two corresponding sides of triangles $\triangle OPQ$ and $\triangle OAB$ are equal,
$\displaystyle\frac{OP}{OA}=\frac{OQ}{OB}=\frac{1}{4}$.
And the angle between the pairs of sides also equal. So the two Triangles are similar with the ratio of all three corresponding sides equal to $\frac{1}{4}$.
Ratio of the two bases $PQ$ and $AB$ is,
$\displaystyle\frac{PQ}{AB}=\frac{1}{4}$,
$\Rightarrow PQ=\frac{1}{4}AB=2.5$ cm.
Let us show you the sketch now, though it is not really required.
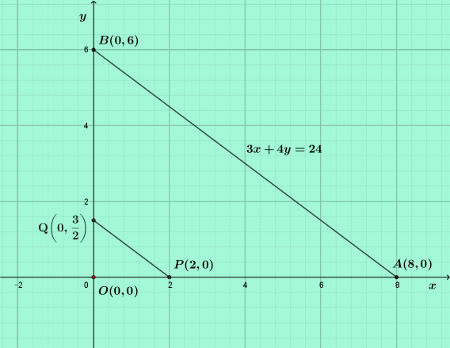
Verify the explanation from the figure.
Why did we solve the problem in mind rather than draw the simple sketch on paper?
Reason is in the Mechanism of learning,
If you make it a habit, at least during practice sessions, to think out solutions in mind touching pen to paper the least, your mental skill in visualizing, manipulating and analyzing ideas get stronger.
The sketch acts in this case like a crutch which slows you down.
The quick way to solve
But why would you take so much trouble in dealing with similarity of triangles at all!
If you can identify the triangle $OPQ$ as a standalone right-triangle with base as $2$ cm and height as $\frac{3}{2}$ cm, by Pythagoras theorem you get the length of the hypotenuse $PQ$ immediately,
$PQ=\sqrt{2^2+(\frac{3}{2})^2}=\displaystyle\frac{5}{2}=2.5$ cm.
It is problem solving with the resources given based on basic concepts that you have and solving in the minimum number of steps taking shortest time.
Answer: Option b: $2.5$ cm.
Key concepts used: Graphical representation of a linear equation -- Graphical solution of algebraic problems -- Key pattern identification -- Pythagoras theorem -- Solving in mind.
Q5. If $ab+bc+ca=8$, and $a^2+b^2+c^2=20$, then a possible value of $\frac{1}{2}(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]$ is,
- $80$
- $84$
- $72$
- $56$
Solution 5: Quick solution: Three variable square of sum and suitable use of given information
First to evaluate $(a+b+c)$ from the first two given equations, as it is needed in target evaluation,
$(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)=20+16=36$,
$\Rightarrow (a+b+c)=6$.
Time to expand the second factor of the target,
$E=3[2(a^2+b^2+c^2)-2(ab+bc+ca)]=6\times{(20-8)}=72$.
Solution is quick.
Answer: Option c: $72$.
Key concepts used: Three variable square of sum — Simplification using given information -- Solving in mind.
Q6. If $a+b+c=m$, and $\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}+\displaystyle\frac{1}{c}=0$, then average of $a^2$, $b^2$ and $c^2$ is,
- $\displaystyle\frac{m^2}{3}$
- $\displaystyle\frac{m^2}{9}$
- $m^2$
- $\displaystyle\frac{m^2}{27}$
Solution 6: Quick solution by Use of given resource information to evaluate component expressions in the expansion of three variable square of sum
Average of $a^2$, $b^2$, and $c^2$ needed is,
$\displaystyle\frac{a^2+b^2+c^2}{3}$.
Identify the key information that value of $ab+bc+ca=0$ from second given equation,
$\displaystyle\frac{1}{a}+\displaystyle\frac{1}{b}+\displaystyle\frac{1}{c}=0$,
$\Rightarrow \displaystyle\frac{ab+bc+ca}{abc}=0$
$\Rightarrow ab+bc+ca=0$.
From three variable square of sum get the average you need,
$(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)=m^2$, given,
$\Rightarrow a^2+b^2+c^2=m^2$,
$\Rightarrow \text{Average required }=\displaystyle\frac{m^2}{3}$.
Answer: Option a : $\displaystyle\frac{m^2}{3}$.
Key concepts used: Use of given resource information to evaluate component expressions in the expansion of three variable square of sum -- Solving in mind.
Q7. If $a+b+c=9$, $ab+bc+ca=26$, $a^3+b^3=91$, $b^3+c^3=72$ and $c^3+a^3=35$, then what is the value of $abc$?
- $42$
- $24$
- $36$
- $48$
Solution 7: Quick solution by key pattern identification, Collection of like terms together, two-factor expansion of three variable sum of cubes and expansion of square of sum of three variables
From the five equations it is easy to see that the two-factor expansion of three variable sum of cubes is to be used for evaluating $abc$,
$a^3+b^3+c^3=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)+3abc$...........(1)
Now identify the key pattern of getting $(a^3+b^3+c^3)$ by adding the last three equations together. Result is,
$2(a^3+b^3+c^3)=91+72+35=198$,
$\Rightarrow a^3+b^3+c^3=99$.
Substituting in equation (1),
$99=9(a^2+b^2+c^2-26)+3abc$...........................(2)
You'll get $(a^2+b^2+c^2)$ easily from the three variable square of sum,
$(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)$,
$\Rightarrow a^2+b^2+c^2=81-2\times{26}=29$.
Substituting this value in equation (2),
$abc=33-3(29-26)=33-9=24$
Answer: Option b: $24$.
Key concepts used: Key pattern identification -- Collection of like terms together -- Three variable sum of cubes expansion in two-factor form -- Three variable square of sum expansion -- Solving in mind.
Q8. If $x=\sqrt[3]{x^2+11}-2$, then the value of $(x^3+5x^2+12x)$ is,
- $0$
- $11$
- $7$
- $3$
Solution 8: Quick solution by matching target expression with rearranged and cubed given expression
To match the target expression, first rearrange the given equation and then only raise it to its cube,
$x=\sqrt[3]{x^2+11}-2$,
Or, $x+2=\sqrt[3]{x^2+11}2$.
Now raising the equation to its cube,
$x^3+6x^2+12x+8=x^2+11$
$\Rightarrow x^3+5x^2+12=3$.
Answer: Option d: $3$.
Key concepts used: Matching target expression with rearranged and cubed given expression -- Solving in mind.
Q9. If $a^3+3a^2+9a=1$, then what is the value of $a^3+\displaystyle\frac{3}{a}$?
- $31$
- $24$
- $26$
- $28$
Solution 9: Quick solution by Reverse target expression evaluation and Continued factor extraction technique
The given or the target expression neither amenable to discovery and exploitation of any useful pattern, the ULTIMATE method decided to follow is Reverse target evaluation by Continued factor extraction technique.
It would give assured and quick solution.
Assume target expression equal to a dummy value $p$,
$a^3+\displaystyle\frac{3}{a}=p$,
Or, $a^4-pa+3=0$.
We'll extract the factor of $a^3+3a^2+9a$ from this transformed target expression in steps by continued factor extraction technique (which is equivalent to algebraic division) replacing the factor by 1 at each step.
We are sure of quick clean solution as the choice values indicate so.
Consuming highest terms $a^4$ in the first step,
$a(a^3+3a^2+9a)-(3a^3+9a^2)-pa+3=0$
Or, $-3a^3-9a^2-pa+a+3=0$.
Taking one more step consuming $-3a^3$ this time,
$-3(a^3+3a^2+9a)+27a-pa+a+3=0$,
Or, $28a=pa$,
Or, $p=28$.
As expected a clean solution.
Answer: Option d: $28$.
Key concepts used: Reverse target expression evaluation -- Continued factor extraction.
Intuitive solution
You may solve this awkward question very quickly just by trying $a=3$ in the given equation to verify that this value of $a$ satisfies the equation.
With $a=3$ target expression value is, $27+1=28$. This would be an intuitive solution that is always the quickest though not always assured that you would indeed reach the solution this way.
Q10. If $x+3y-\displaystyle\frac{2z}{4}=6$, $x+\frac{2}{3}(2y+3z)=33$ and $\frac{1}{7}(x+y+z)+2z=9$, then what is the value of $46x+131y$?
- $414$
- $464$
- $364$
- $384$
Solution 10: Quick solution by Strategy of elimination of fraction coefficients and Target matching the simplest way
By a brief scan over the equations, we found not only the equations to be purposely made awkward but do not also have any hidden pattern to exploit for quick solution. As a strategy, in this situation the best action is to get rid of the denominators of fractions of all the equations.
Accordingly the equations are transformed to,
$4x+12y-2z=24$
Or, $2x+6y-z=12$............................(1)
$3x+4y+6z=99$...........................(2)
$x+y+15z=63$.............................(3)
To have the target without $z$ we have to eliminate $z$ from the three equations. What is the best way to do this?
$z$ appears with negative coefficient of $-1$ in only equation (1) whereas the sum of the coefficients of $z$ in equations (2) and (3) is 21. So if we multiply the equation (1) by 21 and add the result with equation (2) and equation (3), $z$ will be eliminated.
This is the simplest way to eliminate $z$ it seems.
Taking these actions not surprisingly we get,
$x(42+4)+y(126+5)=252+162=414$.
Answer: Option a: $414$.
Key concepts used: Strategy of elimination of fraction coefficients -- Strategy of finding the simplest way to eliminate $z$ to meet target expression requirement -- solving in mind.
Though the question looks very awkward, with right strategy and its implementation, solution is clean and quick.
Concepts and techniques summary
The concepts and techniques used for quick solution of the questions are,
Two factor expansion of sum of cubes, Comparison of coefficients of like terms, Abstraction technique, Dummy variable substitution, Reverse three variable zero sum principle, Principle of collection of like terms, Reverse target expression evaluation, Continued factor extraction technique, Fraction elimination strategy, Target matching, Factorization of three variable sum of cubes, Graphical representation of a linear equation, Graphical solution of algebraic problems, Compound variables, Strategic problem solving.
Guided help on Algebra in Suresolv
To get the best results out of the extensive range of articles of tutorials, questions and solutions on Algebra in Suresolv, follow the guide,
The guide list of articles includes ALL articles on Algebra in Suresolv and is up-to-date.