
Sudoku Hard Strategies and Techniques: Hard Sudoku level 4 game 1 solution
Learn Sudoku hard strategy and techniques while solving Sudoku hard level 4 game 1. Breakthroughs by DSA, Cycle, Single digit lock explained clearly.
Sections are,
- Sudoku hard level 4 game 1
- Sudoku hard Strategy and techniques for easy solution
- What is a Cycle and how to use it in solving a Sudoku hard puzzle
- How a single digit candidate valid cell is identified by Digit Subset Analysis (DSA) in solving a Sudoku hard puzzle
- How digits possible for all empty cells (DSs) enumerated while solving a Sudoku hard puzzle
- Single digit lockdown and its use in solving a Sudoku hard puzzle
- Sudoku hard technique of double digit scan.
- Sudoku hard technique of parallel scan for a single digit on a row or a column.
- Solving Sudoku hard level 4 game 1 by Sudoku hard strategy and techniques.
You may move directly to any of the above sections by clicking its link and return to previous position by clicking on browser back button.
While going through the solution you may click on say Cycle whenever it appears, to know how to form and use a Cycle and then return to the previous position to continue through the solution.
In the same way, for the other techniques also you may jump to details of a technique and after refreshing your concept return to the point from where you jumped.
Sudoku hard level 4 game 1
Following is the Sudoku puzzle that should engage you for some time. The Rs are the row labels, Cs are the column labels and we define this as the stage 1 marked on top left corner.

Next five sections are on strategies and techniques for solving hard Sudoku puzzles in brief.
To skip these five sections and move straight to the step by step solution of the Sudoku hard puzzle, click here.
Please spend your time on the game before going through the solution.
Sudoku hard Strategy and techniques for easy solution
As a strategy we always try first—the row-column scan to find the valid cell at any stage. This is the most basic and easiest of all techniques.
When easy breaks by row-column scan becomes hard to get, the next technique of Digit Subset Analysis is used.
It is—identification of single valid digit for a cell by Digit Subset Analysis or DSA in short. This technique is explained in a following concept section.
And wherever possible, Cycles are formed. A Cycle is a treasure to have in any situation and Cycles play a key role in quick solution. Concept and use of Cycles are explained in a following section.
You may wait for Cycles to form automatically in a column or row, but a proactive approach of forming a Cycle by DS analysis speeds up the solution process considerably.
The last resort of filling each empty cell with valid digit subsets is to be taken up when it is absolutely necessary. This is a time-consuming and error-prone job. Strategically for faster solution, it is better to delay this time-consuming task as much as possible.
Full DS population process is explained in a following section. Experienced Sudoku players may do it as a routine.
In hybrid strategy, a few of the cells of interest are filled with DS of shorter length and analyzed for a breakthrough such as forming a Cycle.
One of the most powerful patterns that we have used for highly positive result each time, is the lockdown of a single digit in a row or column inside a 9 cell square. It eliminates the digit from all other DSs in the locked row or column outside and inside the 9 cell square. The single digit lockdown technique is also explained in a following section.
A still rarer pattern is 4 cell single digit lockdown in a rectangular formation that we have found only once. Naturally, it is a superset of the single digit lockdown and so is much more effective.
The main strategy should always be to adopt the easier and faster technique and path to the solution by looking for key patterns all the time. Digit lockdown, Cycles, Valid cell by DSA are some of the most important key patterns.
Main strategy for solving a hard Sudoku puzzle is to use the technique that would produce best results quickest. Easy to say, not so easy to do—comes with practice.
What is a Cycle and how to use it in solving a Sudoku hard puzzle
Form of a Cycle:
In a Cycle, the digits involved are locked within the few cells forming the cycle. The locked digits can't appear in any other cell in the corresponding zone outside the few cells forming the cycle.
For example, if a 3 digit cycle (4,7,8) in column C2 is formed with a breakup of, (4,7) in R1C2, (4,7,8) in R5C2 and (7,8) in R6C2, the digits 4, 7 and 8 can't appear in any of the vacant cells in column C2 further.
If we assume 4 in R1C2, you will find R5C2 and R6C2 both to have DSs (7,8) implying either digit 7, or 8 and no other digit to occupy the two cells. This in fact is a two digit cycle in the two cells. Together with 4 in R1C2, the situation conforms to only digits 4, 7 and 8 occupying the set of three cells involved in the cycle.
Alternately if we assume 7 in R1C2 (this cell has only these two possible digit occupancy), by Digit Subset cancellation we get, digit 8 in R6C2 and digit 7 in R5C2 in that order repeating the same situation of only the digits 4,7 and 8 to occupy the set of three cells.
Effectively, the three digits involved cycle within the three cells and can't appear outside this set of three cells.
This property of a cycle limits the occupancy the cycled digits in other cells of the zone involved (which may be a row, a column or a 9 cell square). This generally simplifies the situation and occasionally provides a breakthrough by reducing the number of possible digits in the affected cells.
A number of Cycles are shown from a later stage of Sudoku solution:

Cycle (1,2,6) in column C1 is over all three 9 cell squares on the left. It affects only the column C1.
Cycle (3,8,9) in top right 9 cell square is also in row R2, so it should affect both the 9 cell square and R2.
But Cycle (3,6,7) in top right 9 cell square is formed only in the 9 cell squares, it affects only the cells in the 9 cell square.
Can you see another Cycle in row R1 apart from Cycle (1,6)? The second Cycle (3,6,7) is formed by the cells R1C2, R1C3 and the far away cell R1C9. This Cycle affects only the row R1.
Can you say which are the affected areas for Cycle (1,6) in R1?
Two cells of this Cycle belong to row R1 as well as to the top middle 9 cell square. So the Cycle affects two areas, the row and the 9 cell square. This will be true for any two digit Cycle.
Use of a cycle:
In the example of cycle described above, if a vacant cell R8C2 in column C2 has a possible DS of (1,4), as digit 4 has already been consumed in the cycle (4,7,8) in the column, only digit 1 can now be placed in R8C2. You get a single valid digit 1 for R8C2.
This is how a new valid cell is obtained using a Cycle that was not visible otherwise.
In any hard Sudoku game solution, creating, analyzing and using the pattern of Cycles play a very important role.
How a single digit candidate valid cell is identified by Digit Subset Analysis (DSA) in solving a Sudoku hard puzzle
Sometimes when we analyze the DSs in a cell, especially in highly occupied zones with small number of vacant cells, we find only one digit possible for placement in the cell. We call valid cell identification in this way as Digit Subset Analysis.
For example, if in row R4 we have four empty cells, R4C1, R4C3, R4C6 and R4C9 with digits left to be filled up [1,3,5,9] we say, the row R4 has a DS of [1,3,5,9]. After forming this valid digit subset for the row R4, it would next be analyzed for against each of the four empty cells to find the individual empty cell DSs in row R4.
After forming the DS [1,3,5,9] for row R4 when DS in R4C1 is analyzed, if we find that digits [3,5,9} appear in its other two parent zones, the left middle 9 cell square and column C1, the three digits 3,5 and 9 are eliminated from the DS leaving the lone digit 1 valid for the cell.
This is how we identify a valid cell by Digit Subset Analysis.
You may also refer to our first and second game play sessions at level 2 where we first explained use of a Cycle and DSA.
How digits possible for all empty cells (DSs) enumerated while solving a Sudoku hard puzzle
We have not yet discussed the enumeration of every empty cell with their valid digit subsets or DSs.
Let us see this in a little detail. We'll enumerate the possible digit subset or DS for empty cell R8C1 in the following Sudoku game.
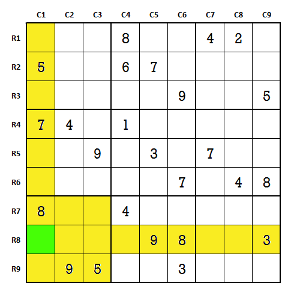
Target cell R8C1 is colored green. Unique set of digits in the three zones—bottom left 9 cell square, row R8 and column C1 colored yellow—will determine the DS for empty cell R8C1.
To enumerate the DS for cell R8C1, look at the row R8 with six digits missing in it—1, 2, 4, 5, 6 and 7.
Now cross-scan column C1 to identify any of these six appearing in column C1.
As 5 and 7 are the two digits out of six that are missing in the intersecting row R8, cancel these two from the six digit subset for R8C1 to reduce it to [1,2,4,6]. Considering row R8 and column C1, possible digits that can occupy R8C1 till now are the DS [1,2,4,6].
But R8C1 also belongs to a 9 cell square and filled digits in it will affect the DS for the cell.
So lastly check the third dimension of the home square, the 9 cell bottom left square, for any more possible digit cancellation.
With no additional digit cancellation, the valid digit subset or DS for the cell would be four digits [1,2,4,6].
None of these four digits appear in the home square, home column or the home row for the cell R8C1.
Basically for evaluating the valid DS for a cell,
You have to cross-scan the row and column as well as check against the home square digits to identify the missing digits that may fill the cell.
This is a tedious and error-prone process.
In solving a hard Sudoku puzzle, there may be no option than to go through the full empty cell DS evaluation.
But it should be done when it has to be done and as late as possible.
Two strategic approaches are adopted to minimize the overall work load in this process—
- First try to find valid digits and fill the cells as much as possible using any technique so that the number of possible valid digits in empty cells as well as number of empty cells are reduced, and,
- Identify promising zones to evaluate the small DSs of a few cells trying for a breakthrough and so reduce the full DS evaluation load.
The second is a dynamic approach that depends on your experience and skill in identifying promising zones.
Single digit lockdown and its use in solving a Sudoku hard puzzle
Occasionally, after evaluating valid DSs for a number of empty cells, you may find that,
A single digit appears only in the DSs of two or three cells in a 9 cell square, in a column or a row, and in no other DSs in the 9 cell square.
This is what we call as single digit lockdown.
If it happens in a row (or a column) inside a 9 cell square, the digit cannot appear in any other cell in the row (or the column) outside the square.
This eliminates all occurrences of the locked digit from the DSs in the row (or the column) outside the 9 cell square. Usually it creates a much needed breakthrough. It is a very powerful pattern.
Single digit lockdown - Conditions for single digit lockdown - how to identify it
Two conditions for single digit lockdown pattern,
- the digit can be placed in only two or three cells of a column or a row, AND,
- the locking cells must also be in SAME 9 cell square.
The third desired condition is,
- The lockdown to be effective, the locked digit should not be present as a single cell candidate in both the adjacent two 9 cell squares through which the locked column or row passes.
The following shows an example of single digit lockdown of 5 in cells R7C1 and R9C1.

How a single digit lockdown is formed
Look at columns C1, C2 and C3 in the bottom left 9 cell square R7R8R9-C1C2C3. Out of 3 empty cells, the cell R7C3 is debarred for placing digit 5 as column C3 has a 5 and it lights up the cell for digit 5.
5 can appear only in two cells in column C1, R7C1 and R9C1 and in no other cell in the 9 cell square or the column C1.
It is locked inside these two cells in C1 and 9 cell parent square.
How a Sudoku single digit lockdown is used - What it does
The locked digit 5 eliminates itself from the DSs of the other two empty cells R5C1 and R6C1 and a new Cycle (2,3) is created in C1.
Focus again on the bottom left 9 cell square. With Cycle (2,3) in C1, another Cycle (5,9) is formed in the two cells of the 9 cell square. As a result, digit 1 becomes the only digit left and cell R7C3 only cell left for it in the 9 cell square.
Still more happens. With 1 in C3 now, digit 9 now must occupy the cell R6C3.
These two single digit candidates obtained by the single digit lockdown of 5 affects other cells and breaks the bottleneck.
As a strategy, always form a single digit lock as soon as it is discovered.
You may think, what is the point of it, what would it achieve after all!
Well, in a similar situation in the process of solving a hard Sudoku puzzle game, the reduced DS in R9C1 formed a cycle (3,7) in column C1 and helped to pinpoint a valid digit 4 in cell R2C1 and that started a deluge of valid cell finds. This proved to be the key turning point in the whole game.
Sudoku hard technique of Double digit scan
This technique sounds simple, but being aware of its existence and identifying it would always result in an important breakthrough. This digit pattern usually occurs in very hard Sudoku.
We will explain this advanced Sudoku hard technique on the following situation in a Sudoku hard game,

Notice the two highlighted digits [1,6] appearing in both row R4 and C5. Together these two result in DIRECT FORMATION OF CYCLE (1,6) in central middle 9 cell square.
This is a double digit scan simultaneously on a row and a column.
Now observe a second set of highlighted double digits [3,9] in C5 which DIRECTLY FORMS TWO CYCLES (4,7,8) AND (3,9) IN CENTRAL MIDDLE 9 CELL SQUARE.
This is a double digit scan on a single zone of C5.
Finally, with 3 in C4, R4C4 9 and R4C6 3.
Together these two double digit scans have produced two valid cells and two Cycles. It is a major breakthrough early in the Sudoku hard game.
Sudoku hard technique of Parallel scan
A parallel scan is carried out for a specific digit on the empty cells of a promising row (or column). Because of presence of the specific digit in the interconnecting columns (or rows) for all empty cells of the scanned row (or column) except one, the valid cell for scanned digit can be identified as this cell.
The digit pattern and the technique to identify a breakthrough valid cell by parallel scan is shown in the figure below,

The parallel scan for digit 6 is done in this case on the empty cells of R1. Out of 4empty cells R1C4, R1C6, R1C7 and R1C9, digit 6 is disallowed in the first two by 6 in top middle major square and disallowed in R1C7 by 6 in C7.
This leaves only the single cell R1C9 where digit 6 can be placed. That becomes the valid cell for digit 6.
Observe that as a result a Cycle (4,7,9) is formed in the rest of the three empty cells in R1.
If you could have identified the Cycle before parallel scan, you could automatically have got the valid cell without parallel scan. That's the interesting property of parallel scan, if you can spot one, you would be sure to find an equivalent Cycle as a result.
To us, valid call by parallel scan is easier and faster.
Let's solve the puzzle now.
Solving Sudoku hard level 4 game 1 by Sudoku hard strategy and techniques
We'll show the hard Sudoku game again for ease of explanation.
To follow the details accurately, you should better have the game actually with you written on paper, or still better—created in a spreadsheet.

The first valid cell identified is—R3C4 3, scan C5, C6—pretty simple. This first fill in a stage is colored turquoise blue as a convention.
Next few valid cells obtained by direct scans are—
R9C9 4, scan R7,C7,C8 -- R5C6 4, scan R4,R6,C4 -- R5C6 4, scan R4,R6,C4 -- R3C5 4, scan R1,C6 -- R2C3 4, scan R1,R3,C2 -- R8C1 4, scan R9,C2,C3.
Digit 4 is fully populated in all 9 cell squares, and good thing is Cycle (1,5) is automatically formed in cells R1C5 and R1C6 in R1 because of cancellation of 2 in R1 from DS [1,25] in both the cells. Next fill by exclusion is—
R2C6 2.
As a strategy, we don't delay in identifying a Cycle and reaping its benefits immediately.
We take up cross-scan again to get the next few fills as—
R4C5 8, scan R6,C4,C6 -- R5C2 8, scan R4,R6,C1 -- R3C3 8, scan R1,C1,C2 -- R1C1 9, scan R3,C2,C3 -- R6C2 5 scan C1, C3.
Now we force-create the 3 cell Cycle (1,2,6) in cells R3C1, R5C1 and R9C1 by Digit Subset Analysis or DSA in these 3 cells—
For R5C1 DS [1,2,6] as, digit 5 is cancelled by scan in C1 from the DS [1,2,5,6] in R5 -- For R3C1 DS [1,2,6] as, digit 7 is cancelled by scan in C1 from DS [1,2,6,7] in R3 -- For R9C1 DS [1,2,6] as digits [3,7] are cancelled from DS [1,2,3,6,7] in R9C1 home square by cross-scan in C1 and R9.
This is a minor breakthrough that resulted in—
R6C1 3 by exclusion.
Before we close this stage
Cycle (1,6,7) formed in top right 9 cell square -- Cycle (3,8,9) formed in R2 in same square -- R2C2 1 by exclusion.
A lot has been achieved at this stage with formation of many Cycles and valid cell fills.
The results are shown below with valid cells found at this stage colored green. We'll color the valid cells in the next stage in a different color to distinguish the cells filled in various stages.

Stage 3 of Sudoku hard puzzle solution: level 4 game play 1
The immediate positive results are—
R2C9 9 as 8 cancelled by scan on C9 from DS [8,9] -- Cycle (2,6) in R4C9 and R4C9 in R4 by cancellation of 9 from DS [2,6,9] in R4C9 -- R4C6 5 by cancellation of 6 due to cycle (2,6) from DS [5,6] in R4C6 -- R1C6 1, DS cancel -- R1C5 5 by cancellation -- R7C6 6 exclusion -- Cycle (1,2) in R7C5, R9C5 -- R8C4 5, scan R9, C5 -- R5C4 2, DS cancel of 5 from DS [2,5] -- R9C4 7 exclusion -- digits [1,2] cancelled in DS [1,2,6] in R6C5 -- R6C5 6.
And then—
Cycle (1,6) in R5, R5C8 5 by exclusion -- R7C7 5, scan R8,R9,C8,C9 -- R7C8 9, scan R8,R9,C9 -- R4C7 9, scan R6,C8,C9 -- Cycle (2,6) in R4 -- R4C8 3 by exclusion -- R2C8 8, DS cancel -- R2C7 3, exclusion in R2 -- R9C8 8 scan R7, R8, C8.
We'll close actions of this stage and show you the results below.

Stage 4 of Sudoku hard puzzle solution: level 4 game play 1
Three digits 4, 8, and 9 fully filled, six digits are left with not many empty cells. But there is no easy valid fill even at this late stage. This is the hallmark of a hard puzzle.
The bottleneck is now broken through by the rare and powerful single digit lock discovery—
The single digit 6 is locked in C9 of 9 cell right middle square (because of 6 in R6C5) -- it follows, no 6 can occur in C9 outside this 9 cell square -- R1C9 7 by cancellation of locked 6 from its DS [6,7].
This is the much needed CRITICAL BREAKTHROUGH. The immediate positive results are—
Cycle (3,6) in R1C2, R1C3 -- R3C1 2 by cancellation of 6 from DS [2,6] -- R3C2 7 by exclusion-- Cycle (1,6) in R9, R9C5 2 by exclusion -- R7C5 1 exclusion.
The rest fills are straightforward as all bottlenecks are overcome. We'll show the rest of routine fills in the last stage. The crucial results of current stage is shown below.
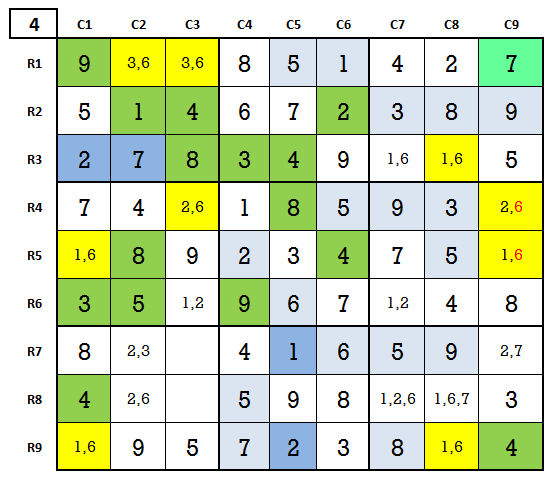
Final Stage 5 of Sudoku hard puzzle solution: level 4 game play 1
The first fill at this stage is achieved by a Cycle—
Cycle (1,6) in R3C8 and R9C8 of C8 -- R8C8 7 by exclusion.
And subsequent fills—
R7C9 2 by cancellation -- R4C9 6 by cancellation -- R5C9 1 by exclusion -- R5C1 6 by exclusion -- R4C3 2 exclusion -- R9C1 1 exclusion -- R9C8 6 exclusion -- R3C8 1 exclusion -- R3C7 6 exclusion -- R6C3 1 exclusion in 9 cell square -- R6C7 2 exclusion -- R8C7 1 exclusion -- R7C2 3 cancellation of 2 from DS [2,3] -- R7C3 7 exclusion -- R1C2 6 cancellation of 3 from DS [3,6] -- R8C2 2 exclusion.
Lastly—
R8C3 6 exclusion -- R1C3 3 exclusion.
The final solved game board is shown below.

Check for the validity of the solution if you need.
End note on Problem solving in Sudoku
Any puzzle solving involves essentially problem solving. The general steps are,
- First stage analysis and breaking it down into smaller chunks if possible as well as adapt the strategy of solving this type of problem,
- Solving the easier component problems so that the main problem size and complexity is reduced,
- Detailed information collection, that is, defining the problem in more details as far as possible,
- Second stage analysis of structure of problem (in this case of Sudoku) and information content,
- Key pattern identification,
- Use of the key pattern to create the breakthrough,
- Repeating the last four steps (steps 4, 5, 6 and 7) for finally solving the problem.
As this Sudoku problem is large and complex, we had to stop at step 3 to collect detailed DS information of most of the empty cells avoiding longer length DSs. Too much clutter makes it difficult to spot patterns.
The breakthroughs were by force-creating or normal formation of Cycles and single digit lockdown.
Digit subset analysis remained a necessary part practically for taking any action.
Level of hardness being high in this puzzle, careful attention to details was needed most of the time.
Checkout and tally these seven steps with the process of solving this puzzle.
This is what we call the life cycle of Problem Solving, an independent and enormously powerful overlay subject standing on its own.
Other Sudoku game plays you may like to go through at leisure
If you start at beginner level Sudoku solutions and go through higher levels step by step, you should become an Expert Sudoku solver.
Expert Sudoku: Play and learn how to solve harder Expert level Sudoku puzzles. Many of these are extremely difficult to solve with easy to understand detailed solutions.
Hard Sudoku level 4 games: Selected main category of hard Sudoku puzzles with very detailed solutions. Learn hard Sudoku Strategies and Techniques.
New York Times Hard Sudoku games with compact one-step solutions and a few NYT hard Sudoku games with a little more detailed solutions.
Medium Sudoku level 3: With these games, you really grow up from the beginner level. Learning to solve this level of games will give you confidence to solve really hard Sudoku games of higher difficulty level. Don't skip this level of games while still learning Sudoku. These games are with detailed step by step solutions as well.
Next series of game to play are the main category of hard Sudoku level 4 games with detailed solutions.
Beginner level Sudoku: For beginners, Sudoku beginner level 1 and level 2 game solutions are ideal to start with. Learn to solve easiest Sudoku games and the most basic techniques of finding a hidden single by row column scan and a naked single by possible digit subset analysis (DSA).
Enjoy playing Sudoku.