
Learn new Sudoku techniques while solving the Sudoku level 2 first game
Only beginner level technique of row column scan won't any longer be enough to solve this first game at Sudoku level 2. You'll learn new techniques now.
After proceeding a few steps in solving this game by using row column scan, you will suddenly find that you are no longer able to proceed further.
This is the point where we have to devise new techniques for finding a valid cell based on new logic of pattern analysis.
This is the hallmark of Sudoku game.
As you try to solve increasingly difficult Sudoku problems, you need to create and use more sophisticated pattern analysis techniques.
We will keep open the option for you to devise your own techniques to solve the game. You may solve the game on your own and check the solution given at the end of the session. If you are stuck, you may refer to our step by step solution process.
Or, you may decide to learn the new techniques straightaway from our detailed solution.
The Sudoku level 2 game 1
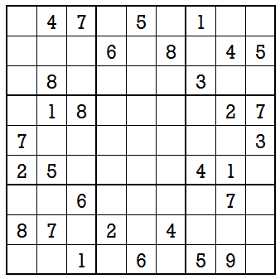
A rough criterion to judge the difficulty level of a Sudoku game is the number of empty cells in the game board. In all our earlier beginner level games, if you had noticed, the number of empty cells was 45 to 47 at most. In this second hardness level game, the number of empty cells is 51, a larger number.
It simply means, there won't be many friendly digits waiting for you to easily form a scan pattern and pinpoint a valid cell. You have to work more intelligently and use more complex techniques to find a valid cell.
Here we will leave you with the game to solve yourself or go forward with our solution.
Solution process of the first Sudoku level 2 puzzle game
To start with we will repeat the very brief Sudoku concepts under Aside 1 and Aside 2. If you are already comfortable in playing easy Sudoku, you may skip these two sections.
Furthermore, If you feel the need to brush up the basics of how to play Sudoku in more details, you may go back to our session 1 and session 2 of beginner level Sudoku game play.
Aside 1:
A Sudoku game board of 81 square cells comes with a few of the cells already filled up with valid digits 1 to 9. The objective of the game is to fill up rest of the empty cells following the basic Sudoku rule of NOT using any of the digits 1 to 9 more than once in any row, column or 9-cell square (identified by thick borders, there are 9 such 9-cell squares).
At each step when we locate a valid cell where we can put one and only one digit, we will identify the cell by its row number (R1 to R9) suffixed by column number (C1 to C9), mention the digit, and mention the column row scan information (or nothing if the cell happens to be only one empty in the containing row, column or 9-cell square).
If we use a new technique to find the valid cell, we will mention the type of technique and if needed will explain it in more details. Sometimes we will add a remark.
The only objective at each step is to find a cell in which one and only one digit can be placed. This is what we call a valid cell.
Aside 2:
Valid cell and Valid digit:
We would repeat the definition of valid digit and the valid cell.
We define a VALID digit as the digit you put in an empty cell so that,
It is the only possible digit which you can put in the cell following the rules of the game.
As before, the most important objective is, how to find out the cell in which you can put one and only one digit out of the digits 1 to 9.
We have used the most basic technique of row column sweep or horizontal-vertical cross-scanning mainly. We have used Exclusion technique wherever we found it possible.
We used the concept of a favorable zone as a column or a row or a 9-cell square with high digit occupancy so the number of digits possible to fill up the empty cells in the zone is much less and so by eliminating the few other contenders getting only a single digit for a single cell is that much higher. We have also used digits with high occurrence in the board, that is, the favorable digits to our advantage.
For a favorable digit that has appeared, say, in 7 cells out of maximum 9 possible all over the board, finding the rest of the two valid cells for this favorable digit by row-column sweep is generally very easy because of elimination of a large part of the board by its occurrence in most zones.
Let's find the valid cells - the stages in solving Sudoku level 2 first game
We will show the game board again for convenience. The following is the Sudoku game we have to solve.
Our strategy will generally be to find a valid cell by row column scan and if it doesn't work then use more powerful techniques. We will stop and explain how a new technique works when we meet it for the first time.
The first step is easy and we get our first three valid cells by scan only. But now after this quick success three times we are stuck. We exhaustively go through all possible scans but with no success.

Valid cell R8C8 3, scan C7, C9 -- R5C8 5, scan C7, C9 -- R2C7 7, scan C8, C9.
The new technique Digit Subset Analysis or DSA in short
For quick success by this technique, we identify a most favorable zone (row, column or a 9-cell square) with highest number of cells filled up so that the possibilities of digits occupying the few empty cells are minimum.
Usually, we get the opportunity to apply this powerful technique quickly on a row or column with 7 cells filled up and only two cells remaining empty. If the empty cells are more than 2, chances of success is less.
In our game such a favorable zone is the column C8. In its two empty cells the two digits 6 and 8 are the only possibilities. These two digits 6 and 8 form what we call the Digit Subset.
Now we will analyze this digit subset by cross checking each of these two empty cells with the intersecting rows to see whether any of the two digits 6 or 8 is appearing in an intersecting row. If we find in an intersecting row all of the digits in the Digit Subset except ONE are already present, we can conclude, that one digit excluded will be the valid digit for the cell being examined. This is the analysis part. First form the Digit Subset and then Analyze. Together, it is Digit Subset Analysis.
In our favorable zone of column C8, when we check the first empty cell R1C8 for occurrence of the digits 6 or 8 in the intersecting row R1, we find none of the two appearing. But next when we check the cell R3C8, we find 8 appearing in the intersecting row R3. It means, out of the two possible digits 6 and 8 in the cell R3C8, 8 already eliminated, only ONE single digit 6 is possible. Thus in cell R3C8 we get valid digit 6. And this is the breakthrough we needed.

So we have, R3C8 6, DSA for [6,8] in column C8 -- R1C8 8 -- R1C1 6, scan R2, R3 -- R5C2 6, scan C1, C3. And again we are stuck.
To try DSA in top right 9-cell square, we form the digit subset [2,9] for cells R1C9 and R3C9, but on analysis we don't get any success as 2 or 9 doesn't appear in any of the rows R1 or R3. But still we keep the information that only 2 or 9 can fill up the cells R1C9 and R3C9. We write this digit subset information in the two cells for the first time. Later we'll find that this will be the first step we would have to take with very hard Sudoku problems.
Concept of Cycle
These two possibilities of 2 and 9 in two cells of column C9 means - in this column 2 or 9 can't appear in any other remaining empty cells. Though at this point of time we don't exactly know in which of the two cells 2 or 9 will appear in C8, but we are sure that 2 and 9 will certainly be appearing only in these two cells and not in any other cell of the column. This is what we call, formation of a Cycle. A cycle of degree 2 is formed with the digit subset [2, 9] in the two cells R1C9 and R3C9.
We will use this cycle in the new Cycle use technique.
Cycle use technique
Let's reproduce the last state of the board with new successes.

Let's focus our attention on the bottom right 9-cell square and search for a place for digit 2. As the three cells in column C9 are out of bounds for 2 because of the cycle [2,9] in C9, and cell R8C7 also illegal for 2 for R8 scan, the only cell left for 2 is R7C7.
We'll color the cell successes by DSA technique light blue and those by Cycle use technique by dark yellow.
Our next few successes are then, R7C7 for 2 with Cycle use technique on C8 and cycle [2,9] -- R9C2 for 2, scan R7, R8, C1.
Next we form a DS of [1,4,6,8] on bottom right 9-cell square and locate valid cell R8C7 for 6, as in R8 and C7 combined, the three digits 1, 4 and 8 appear but not 6. This a good example of applying DSA technique.
Proceeding further, R6C9 for 6, scan C7, C8 -- R4C6 6, scan C4, C5, R5, R6, an unavoidable 4 order scan. The digit 6 is over with this.
Let's go for the next stage.

The successes are, R8C9 1, DSA with DS of [1,7,8] on bottom right 9-cell square and analysis on R8 -- R8C5 9, DSA for DS [5,9] on R8 scan C5 -- R8C3 5 -- R4C7 9, DSA for DS [8,9] on C7, scan against R4 -- R5C7 8 -- R4C4 5, scan R5, R6, C5 -- R7C6 5, scan C4, C5, R9 -- R3C1 5, scan R2, C3 5 over.
In the next stage we form DSs in a few prospective cells which in turn generates cycles and gives us the breakthrough. Let's see how.

We have formed DSs in the cells, R1C4, R1C6; R4C1, R4C5; R2C2, R7C2; and R7C1, R9C1.
After forming these DSs when we analyze the DSs in column C1 we find a cycle of digits [3,4] formed between R4C1 and R9C1 prohibiting the digits 3 and 4 appearing in any other empty cell of C1. Thus, we get valid cell R7C1 for 9 providing us the breakthrough we needed.

We got,
R7C1 9, Cross DSA -- R7C2 3 by DS cancellation or DSC -- R2C2 9 DSC -- R9C1 4 -- R4C1 3 DSC -- R4C5 4 -- R2C1 1 -- R6C3 9, DSA for DS [4,9] on cells R5C3 and R6C3 in the containing 9-cell square -- R5C3 4 -- R3C3 2 DSA for DS [2,3] on cells R2C3, R3C3 resolved across R3 -- R2C3 3 -- R3C9 9 DSC -- R1C9 2 DSC -- Delete 2 in R1C6 DS.
The last action is important. In cell R1C6 even though we are not aable to resolve for single digit, we have reduced the possibility by 1. This is called DS update or DSU in short and is an essential routine action while solving complex Sudoku boards.
Let's now go over to the last stage.

Remaining selections are, R7C9 4, scan R8,R9 -- R9C9 8 -- R2C5 2 -- R5C6 2, scan C4, C5 R6 -- R5C5 1, DSA of [1,9] -- R5C4 9 -- R1C4 3 DSC -- R1C6 9 -- R9C4 7. End. Solved.
A special note for you
We haven't tried to optimize. So we feel that this more complex game is solvable by following an easier path.
You should try to reach one of the simpler solutions.
Lastly, we leave a game for you to solve.
A game for you to solve
We leave you here with a new game for you to solve. In our next session we will present its solution and another new game.
Enjoy.

Other Sudoku game plays at Second level hardness
Sudoku 2nd level game play 1
First level and higher level Sudoku games
You will get links to all the 1st level game solutions at Sudoku level 1.
Links to higher level Sudoku games are available at the main Sudoku page.
It is recommended that without jumping over any of the hardness levels, one should progress through solving higher level Sudoku games strictly step by one step up. For example, you shouldn't play a 4th level Sudoku game without becoming comfortable in solving 3rd level games.