
Solve Hard Sudoku level 3 game 4 by hard Sudoku techniques
In step by step solution of Sudoku level 3 game 4, use of hard Sudoku techniques for breakthroughs such as single digit lock or deformed X wing explained.
Following is the Sudoku level 3 fourth game we'll solve after you solve it first.
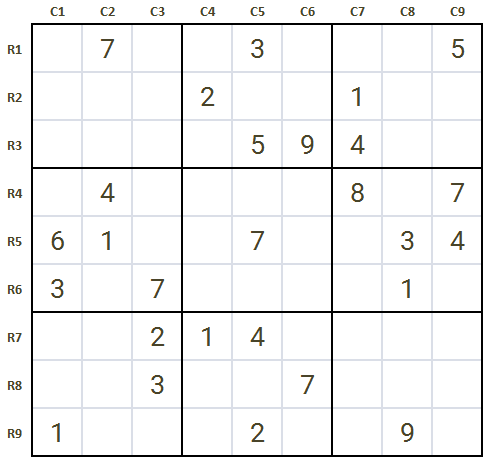
Though number of filled cells in the game is 27, whereas filled cells become as low as 22 in a very hard Sudoku game, this Sudoku level 3 puzzle game 4 is a hard one and needed use of hard Sudoku techniques for breakthroughs.
As a strategy, we'll always try to get a valid cell by row column scan first, by possible digit analysis or DSA second and by reduction caused by Cycles third. Cycles are valuable resources and we'll form a Cycle whenever we get the chance.
In addition we'll also use any other advanced Sudoku techniques of single digit lock, parallel digit scan or X wing if necessary.
Evaluation of possible digit subsets for all empty cells is often prescribed as a must-do activity. We strongly recommend to avoid this time-consuming activity as far as possible and instead go in for filling up the empty cells by unique valid digits using Sudoku techniques needed.
The Sudoku techniques for solving this fourth hard Sudoku level 3 puzzle game are briefly but clearly explained along with the step by step solution.
Let's go through the solution of the game.
Solution to Sudoku level 3 game 4 Stage 1: First breakthrough by deformed X wing digit formation

Starting scan for 1 following conventional scan strategy: R8C9 1 by scan for 1 in R7, R8, C7, C8 -- next scan success is with 4: R8C8 4 by scan for 4 in R7, C7, C9 -- R9C3 4 by scan in R7, R8, C2.
No more scan success for 4, 5 or 6. But we get a scan success for 7: R3C4 7 by scan for 7 in R1, C5, C6 -- R7C1 7 by scan for 7 in R8, C2 -- R2C8 7 by scan for 7in R1, R3, C9 -- lastly R9C7 7 by scan for 7 in R7, R8, C9.
Digit 7 fully filled.
In the changed situation now we get a scan success for 2: R8C7 2 by scan for 2 in R7, R9.
We'll now show the power of special Sudoku digit formation of deformed X wing for a breakthrough.
First form a pair of possible digit 2 in only the two cells R4C1, R6C2 of left middle major square by scan for 2 in C3 (shown by arrow).
Similarly form a second pair of possible digit 2 in only the two cells R4C8 and R6C9 of right middle major square by scan for 2 in C7. These two pairs of possible digit 2s share common rows R4 and R6 to prohibit any occurrence of 2 in other empty cells of these two rows.
This is as if R4 and R6 both have digit 2 and so scanning for 2 in R4, R6 and C4 results in the breakthrough valid cell in R5C6 2.
We have identified the deformed X wing formation of digit 2 that gave us the breakthrough.
An X wing proper consists of two pairs of single possible digits that share same pair of columns and rows prohibiting appearance of the digit in any other empty cell DS.
When such a two pair of same digit formation shares a pair of rows (or columns) and each pair occurs only in these pair of cells in a major square, only the rows (or columns) shared are prohibited for the digit and any occurrence of the digit in the rows (or columns) shared is reduced. The following figure shows the deformed X wing formation in this game.
Game status at this first stage shown below.

We'll explain the formation and use of the deformed X wing and breakthrough caused by it, in a bit more details.
Breakthrough by hard Sudoku technique of deformed X wing
We'll use the following graphic for explanation.

See that the two diagonal arms of X are not of equal length and that indicates deformation of X resulting in common rows R4 and R6 but no common column pairs.
Because of this common rows, in each row, digit 2 can appear only on R4C1 or R4C8 and R6C2 or R6C9.
Either way, 2 must appear in both the rows R4 and R6. This is as if both rows already have a 2 in them. Its effect is prohibition of digit 2 in any other empty cell of row R4 and row R6.
That's how the deformed X wing provides the breakthrough of R5C6 2 by scan for 2 in R4 (common row shared by X wing), 2 in R6 (common row shared by X wing) and 2 in C4.
This is an early breakthrough that opens up the whole game.
If the single 2 in R4C1 were in R4C2 and the single 2 in R4C8 were in R4C9, we would be having a proper X wing with same length of its two diagonals. Its effect naturally is more positive.
By sharing both pairs of rows as well as columns, this X wing formation prohibits appearance of digit 2 in any of the other empty cells of the pair of rows R4, R6 as well as the pair of columns shared C2 and C9.
Recommendation: look for the deformed X wing as it is more common and usually provides a critical breakthrough.
Solution to the Sudoku level 3 game 4 Stage 2: Breakthrough by parallel scan
Opportunistic scan for 1: R1C6 1 by scan for 1 in R2, C4 -- R4C5 1 by scan for 1 in R5, R6, C4, C6 -- and lastly R3C3 1 by scan for 1 in R1, R2, C1, C2.
Digit 1 fully filled.
Next breakthrough is by parallel scan for 3 on empty cells of column C7: 3 in right middle major square eliminates R5C7, R6C7 for 3 and 3 in R1 eliminates R1C7 for 3.
Only R7C7 is left for digit 3: R7C7 3 -- Cycle (6,8) is formed in bottom right major square cells R7C9, R9C9 by DS reduction -- R7C8 5 by DS reduction of [6,8].
A note on Cycle (6,8)
After placing 3 in R7C7, possible digits in the bottom right major square is reduced to [5,6,8], but with 5 in C9, the two cells R7C9 and R9C9 can have only the reduced possible digit subsets of [6,8]. We call this special configuration in these two cells as the Cycle (6,8).
At this point we are not sure of whether 6 or 8 will finally be placed in which of the two cells, but we are certain that taking both cells combined, digits [6,8] will have no uncertainty in placement.
The two digits cycle between the two cells and cannot appear in any other parent zone containing the Cycle.
That's why the two parent zones of the Cycle, the bottom right major square and column C9 cannot have 6 or 8 in their possible digit subsets.
There may be Cycles involving three digits locked in 3 cells in a zone (row, column or major square).
Four or five digit Cycles also appear but are rare and not easy to identify.
Cycles always are valuable assets for simplification of a hard Sudoku game.
Continuing with Stage 2 analysis...
DS in three empty cells of R7 is [6,8,9] and with 9 in C6, DS in R7C6 is [6,8] forming a Cycle (6,8) with R7C9 and giving the valid cell R7C2 9 by reduction.
Parallel scan for 3 on empty cells of column C7: 3 in R1 eliminates R1C7 for 3, and 3 in right middle major square eliminates R5C7, R6C7 for 3 leaving only the cell R7C7 for 3: R7C7 3. This is an important breakthrough.
Result of actions taken at this stage shown below.

A note on parallel scan
Usual scan for a specific digit is done on the empty cells of a MAJOR SQUARE BY IDENTIFYING PRESENCE OF THE DIGIT IN SCANNED COLUMNS AND ROWS INTERSECTION THE MAJOR SQUARE.
But in this variation of parallel scan, scanning is done also for a single specific digit 3 in this case. But instead of examining the empty cells of the target major square, we examine the impact on EMPTY CELLS OF A ROW OR A COLUMN.
In this specific case, we are examining the four empty cells R1C7, R5C7, R6C7 and R7C7.
3 in right middle major square eliminates two empty cells R5C7, R6C7 for 3 and 3 in R1 eliminates R1C7 for 3. Only the fourth cell R7C7 is left where 3 is to be placed.
Usually a parallel scan is associated with formation of a Cycle in the scanned row or column and provides an important breakthrough.
Solution to Sudoku level 3 game 4 Stage 3: Another breakthrough Single digit lock on 6
Because of 6 in C1, 6 can appear in only the two cells R8C2, R9C2 in bottom left major square creating single digit lock on 6 in these two cells in C2.
By single digit lock on 6 in R8C2, R9C2, digit 6 is prohibited in any other empty cells of C2 because one of these two cells must finally have a 6.
The single digit lock is created by DS reduction of 6 in C1 and it removes 6 from possible digit subset [2,3,6,8] in R3C2.
That's why the Cycle (2,3,8) is created in R3.
Breakthrough: Cycle (2,3,8) in R3 results in R3C8 6 by reduction.
DS in two empty cells of C8 [2,8] -- with 8 in R4, R4C8 2 by reduction -- R1C8 8 by exception in C8 -- R6C9 9 by reduction of 5 in C9 and 6 in Cycle (6,8) of C9 -- R5C7 5 by reduction -- R6C7 6 by reduction -- R6C2 2 by scan for 2 in R4 -- R5C3 8 by scan in R4 -- R5C4 9 by reduction -- R6C5 8 by reduction -- R2C5 6 by reduction -- R8C5 9 by exception in C5.
Game status shown below.

A note on breakthrough by Single digit lock
The more frequent form of single digit lock is shown above in R8C2, R9C2. Digit 6 appears only in the possible digit subsets of these two cells in the major square.
In the final solution, one of these two must be present ensuring that digit 6 is prohibited in all other possible digit subsets of empty cells in C2.
As a result, digit 6 is reduced from the possible digit subset [2,3,6,8] to make it [2,3,8] and thus forms the Cycle (2,3,8) with [2,8] in R3C1 and [2,3] in R3C9.
Final outcome is then unique digit placement R3C8 6 by reduction due the Cycle.
If you stop to think for a moment, you would appreciate that the breakthrough could occur only by reduction of 6 from the DS [2,3,6,8] in R3C2 by the single digit lock.
This is the case of an effective single digit lock that actually can create a breakthrough.
Such an effective single digit lock can happen either by scan of a single row or column or by cross-scan of a row and a column.
For example, if the lock on 6 in R8C2, R9C2 were created by 6 in R5C1 of C1 and 6 in R1C3 of C3, we won't have had the opportunity of any reduction of 6 in any empty cell of C2 (because 6 in both left middle and top left major squares eliminated any possible 6 in the empty cells).
So you can conclude that by scan of a digit in two columns or two rows in adjacent major squares cannot form a single digit lock that can be directly effective (it can yet become effective in forming an X wing though).
Solution to the Sudoku level 3 game 4 final stage 4: Finishing off is a formality
DS in R1C4 [4,8] and with 8 in R1C8, R1C4 4 -- R2C6 8 by reduction -- R6C4 5 by reduction -- R6C6 4 by reduction.
R1C3 6 by scan for 6 in R2, C1 and single digit lock on 6 in C2 -- R1C7 9 by reduction -- R1C1 2 by exception -- R3C1 8 by reduction R3C2 3 by reduction -- R3C9 2 by exception in R3 -- R2C9 3 by exception in top right major square.
DS in C4 and hence in R8C4 is [3,6,8]. It reduced by 3 in R8 to DS [6,8] and joins with [6,8] in R7C6 to form a Cycle. This results in R9C4 3 by reduction of [6,8] -- R4C4 6 by reduction -- R8C4 8 by reduction -- R7C6 6 by reduction -- R7C9 8 by exception in R7 -- R9C9 6 by exception in C9.
R8C2 6 by scan for 6 in R9, C1 -- R8C1 5 by exception in R8 -- R9C2 8 by exception in bottom left major square -- R9C6 5 by exception in R9 -- R4C6 3 by exception in C6.
With 5 in R8C2, R4C1 9 by reduction -- R4C3 5 by reduction -- R2C3 9 by exception in C3 -- R2C2 5 by exception in C2 -- R2C1 4 by exception in whole game.
This Sudoku level 3 is a hard Sudoku game to solve.
The final solution is shown below.

A new game for you to solve at Sudoku level 3
We leave you here with a new Sudoku level 3 game to solve.
Enjoy.

More Sudoku hard puzzles you may like to solve and learn how to solve
The updated list of Solutions to level 3, level 4 and NYTimes Sudoku hard puzzle games:
How to solve Sudoku hard puzzle games full list (includes very hard Sudoku).
Enjoy solving Sudoku hard.
By the way, Sudoku hard solution techniques are included with many of the solutions.
Enjoy also learning how to solve Sudoku hard in easy steps.
