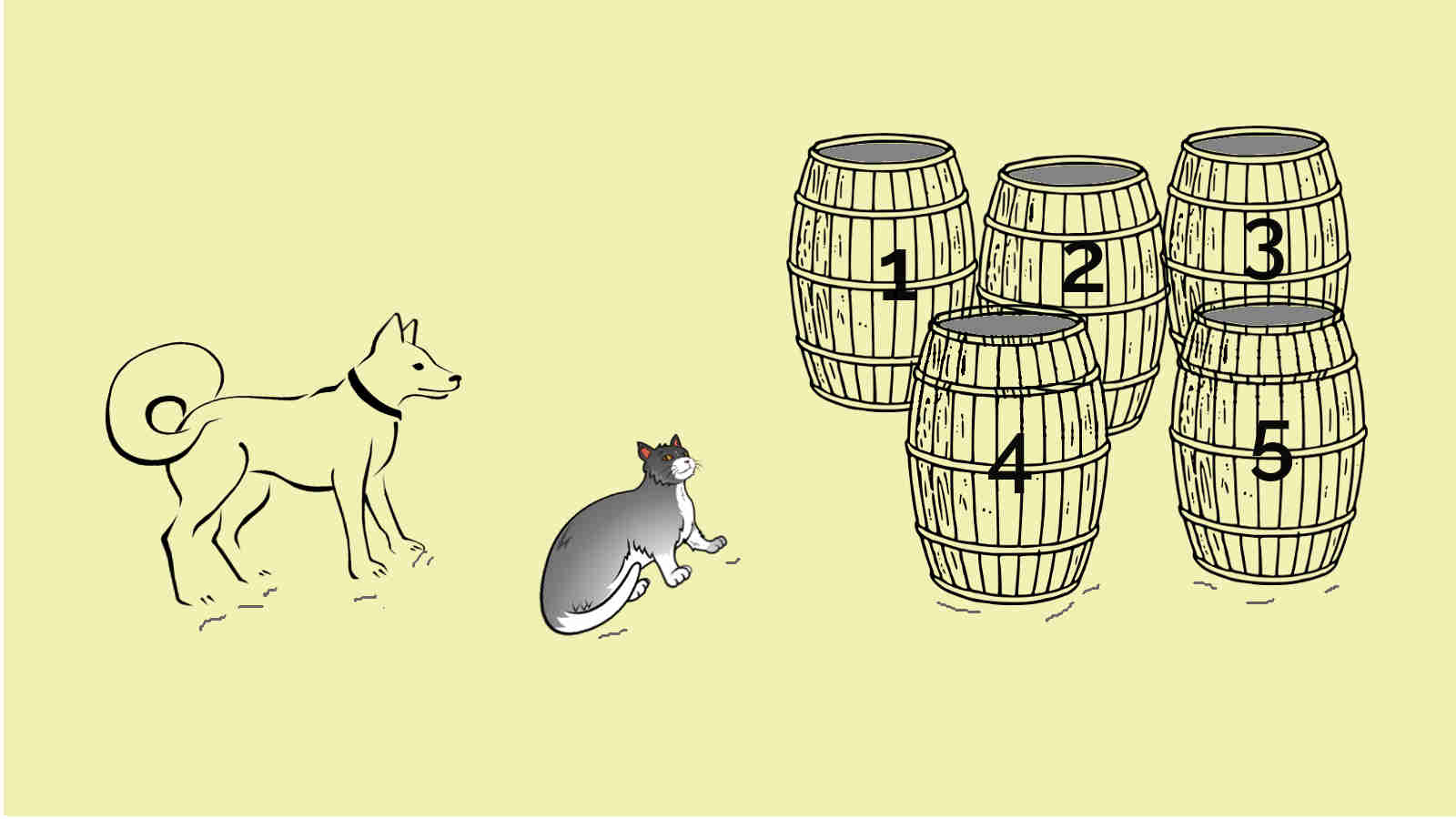
In five barrels a mouse lay hidden. Outside, the dog told the cat, "I know the barrel in which the cat hides!"
The cat asked excitedly, "Which one? Tell me please quick. Today I will catch it for sure."
The dog replied, "Why! It is hiding in the 1000th barrel."
The pussycat looked crestfallen, "How could it be possible? I can see only five."

"You have to count this way." The dog showed,
$1 \qquad 2 \qquad 3 \qquad \text{ }4 \qquad \quad 5$
$9 \qquad 8 \qquad 7 \qquad \text{ }6$
$\qquad 10 \qquad 11 \qquad 12 \qquad 13$......
"So the 8th will actually be the 2nd barrel you see and the 13th will be the 5th you see. Now count. Hurry up." The dog finished his advice.
The cat started counting 1, 2, 3, 4, 5, 6, 7..... and so on and on. In the meantime, the mouse heard everything and was frantically trying to enlarge a hole in its barrel. As expected, just when the cat reached the right barrel, the mouse could make a hole large enough to leap out and escape.
The dog advised, "My dear pussycat, you must learn how to count quick. If you continue this way, you will never catch the mouse. Now go and start learning smart counting."
Can you find the 1000th barrel in 5 minutes or less?
Solution to the Cat and mouse with advisor dog puzzl
The shortest way to reach the 1000th barrel in this case will depend on the extra lines of digits after the first line of five digits.
First conclusion: The number of extra lines of digits must be such that adding 5 to 4 times the number of extra lines should be equal or more than 1000.
How many such extra lines of digits after the first will then be needed? It will simply be 249 as,
$249\times{4} + 5 =1001$ just exceeding 1000.
Second conclusion: The 1000th barrel must then be one left or one right of the last barrel in the last extra line of barrels. If this last line of 998, 999, 1000 and 1001 is counted from left to right, our 1000th barrel will be one left to the 1001st barrel. Otherwise it will be one right to the 1000st one like the second line the dog showed.
Task left then: To determine in which direction the last line numbers increase.
This is also easy.
249th extra line is an odd numbered line. So like the 1st extra line that is odd numbered, the last extra line will also be counted increasing from right to left.
It will be,
$1 \qquad \qquad 2 \qquad \qquad 3 \qquad \qquad 4 \qquad \qquad 5$
$1001 \qquad 1000 \qquad \quad 999 \qquad \quad 998$
The 248th extra line counted upto $4\times{248} + 5 =997$ so that the last line started from 998.
Answer: The mouse was hiding in the second barrel.
Know how to solve difficult problems easily without wasting time on random attempts
Our ebook on puzzle solutions by innovative methods will show you just that.
Puzzles for Adults: 50 Brain Teasers with Step-by-Step Solutions: Boost Your Power of Problem Solving
BUY the never before eBook from Amazon here, from Google Play here and Paperback here.
Puzzles you may enjoy
Easy to hard brain teasers with systematic solutions
Challenging brain teasers with solutions: Long list.
This will always be the most up-to-date full list with the brain teasers classified into categories that can be browsed separately.
You may also click on the category term link below to enjoy the brain teasers that are classified in the present category.
For example, if the category term link shown below is "Riddle", click on it to go through all the Riddles.
