︽

You are here

Home » SSC CGL Tier II »

SSC CGL Tier II level Question Set 11, Trigonometry 2

Submitted by Atanu Chaudhuri on Sat, 26/05/2018 - 23:44

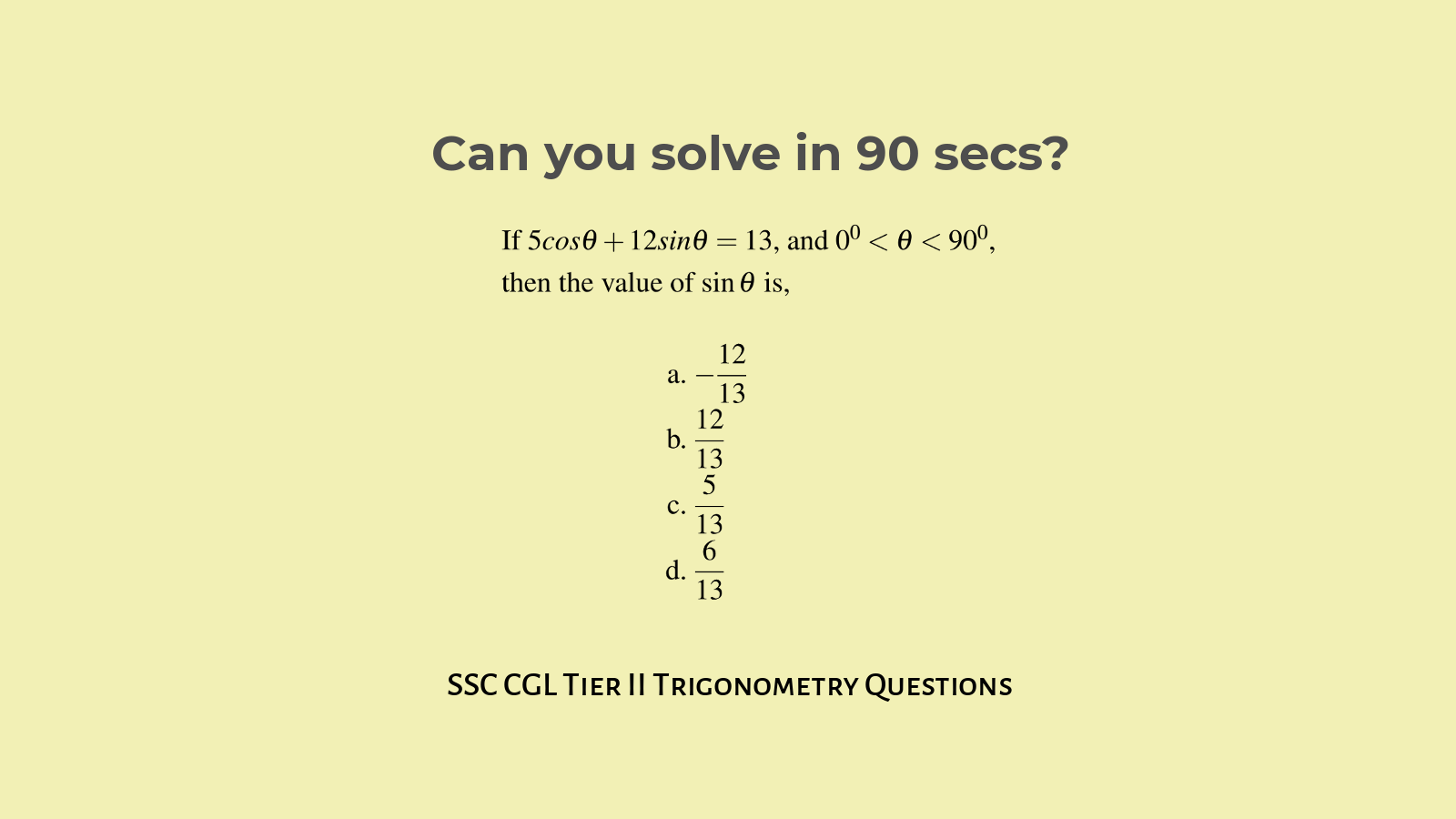
SSC CGL Tier 2 Trigonometry Questions Set 11

SSC CGL Tier 2 Question Set 11 on Trigonometry with answers

Solve 10 selected questions in SSC CGL Tier 2 trigonometry questions set 11 in 12 minutes. Verify results from given answers. Learn to solve from solutions.

Answers and linked solution set are at the end.

SSC CGL Tier 2 Trigonometry Questions set 11 - testing time 12 mins

Problem 1.

If $5 cos \theta +12 sin \theta=13$, and $0^0 \lt \theta \lt 90^0$, then the value of $\sin \theta$,

  1. $-\displaystyle\frac{12}{13}$
  2. $\displaystyle\frac{12}{13}$
  3. $\displaystyle\frac{5}{13}$
  4. $\displaystyle\frac{6}{13}$

Problem 2.

The value of $(cosec \theta -sin \theta)(sec \theta - cos \theta)(tan \theta +cot \theta)$ is,

  1. 1
  2. 2
  3. 4
  4. 6

Problem 3.

If $tan A = n tan B$ and $sin A = m sin B$, then the value of $cos^2 A$ is,

  1. $\displaystyle\frac{m^2+1}{n^2-1}$
  2. $\displaystyle\frac{m^2+1}{n^2+1}$
  3. $\displaystyle\frac{m^2 -1}{n^2+1}$
  4. $\displaystyle\frac{m^2 -1}{n^2-1}$

Problem 4.

If $\theta$ is a positive acute angle and $3(sec^2 \theta + tan^2 \theta)=5$, then the value of $cos 2\theta$ is,

  1. $\displaystyle\frac{1}{\sqrt{2}}$
  2. $1$
  3. $\displaystyle\frac{1}{2}$
  4. $\displaystyle\frac{\sqrt{3}}{2}$

Problem 5.

If $tan \alpha = 2$, then the value of $\displaystyle\frac{cosec^2 \alpha - sec^2 \alpha}{cosec^2+sec^2 \alpha}$ is,

  1. $-\displaystyle\frac{3}{5}$
  2. $-\displaystyle\frac{15}{9}$
  3. $\displaystyle\frac{17}{5}$
  4. $\displaystyle\frac{3}{5}$

Problem 6.

If $\sin (\theta + 30^0)=\displaystyle\frac{3}{\sqrt{2}}$ the value of $cos^2 \theta$ is,

  1. $\displaystyle\frac{1}{2}$
  2. $\displaystyle\frac{1}{4}$
  3. $\displaystyle\frac{3}{4}$
  4. $\displaystyle\frac{\sqrt{3}}{2}$

Problem 7.

$(1 + sec 20^0 + cot 70^0)(1 - cosec 20^0 + tan 70^0)$ is equal to,

  1. $1$
  2. $0$
  3. $-1$
  4. $2$

Problem 8.

If $tan \theta - cot \theta =0$, and $\theta$ is a positive acute angle, then the value of $\displaystyle\frac{tan (\theta+15^0)}{tan(\theta-15^0)}$ is,

  1. $3$
  2. $\displaystyle\frac{1}{\sqrt{3}}$
  3. $\sqrt{3}$
  4. $\displaystyle\frac{1}{3}$

Problem 9.

If $sec \theta - tan \theta=\displaystyle\frac{1}{\sqrt{3}}$, then the value of $sec \theta.tan \theta$ is,

  1. $\displaystyle\frac{2}{3}$
  2. $\displaystyle\frac{4}{\sqrt{3}}$
  3. $\displaystyle\frac{1}{\sqrt{3}}$
  4. $\displaystyle\frac{2}{\sqrt{3}}$

Problem 10.

If $tan (5x - 10^0)=cot (5y+20^0)$, then the value of $x+y$ is,

  1. $15^0$
  2. $16^0$
  3. $20^0$
  4. $24^0$

Answers to SSC CGL Tier 2 Trigonometry Questions set 11

Problem 1. Answer: b: $\displaystyle\frac{12}{13}$.

Problem 2. Answer: a: 1.

Problem 3. Answer: d: $\displaystyle\frac{m^2-1}{n^2-1}$.

Problem 4. Answer: c: $\displaystyle\frac{1}{2}$

Problem 5. Answer: a: $-\displaystyle\frac{3}{5}$.

Problem 6. Answer: c: $\displaystyle\frac{3}{4}$.

Problem 7. Answer: d: 2.

Problem 8. Answer: a: 3.

Problem 9. Answer: a: $\displaystyle\frac{2}{3}$.

Problem 10. Answer: b: $16^0$.

For detailed conceptual solutions please refer to companion SSC CGL Tier II level solution set 11 Trigonometry 2.

Guided help on Trigonometry in Suresolv

To get the best results out of the extensive range of articles of tutorials, questions and solutions on Trigonometry in Suresolv, follow the guide,

Reading and Practice Guide on Trigonometry in Suresolv for SSC CHSL, SSC CGL, SSC CGL Tier II Other Competitive exams.

The guide list of articles is up-to-date.

Trigonometry questions for SSC CGL