SSC CGL level Question Set 77, Trigonometry 7

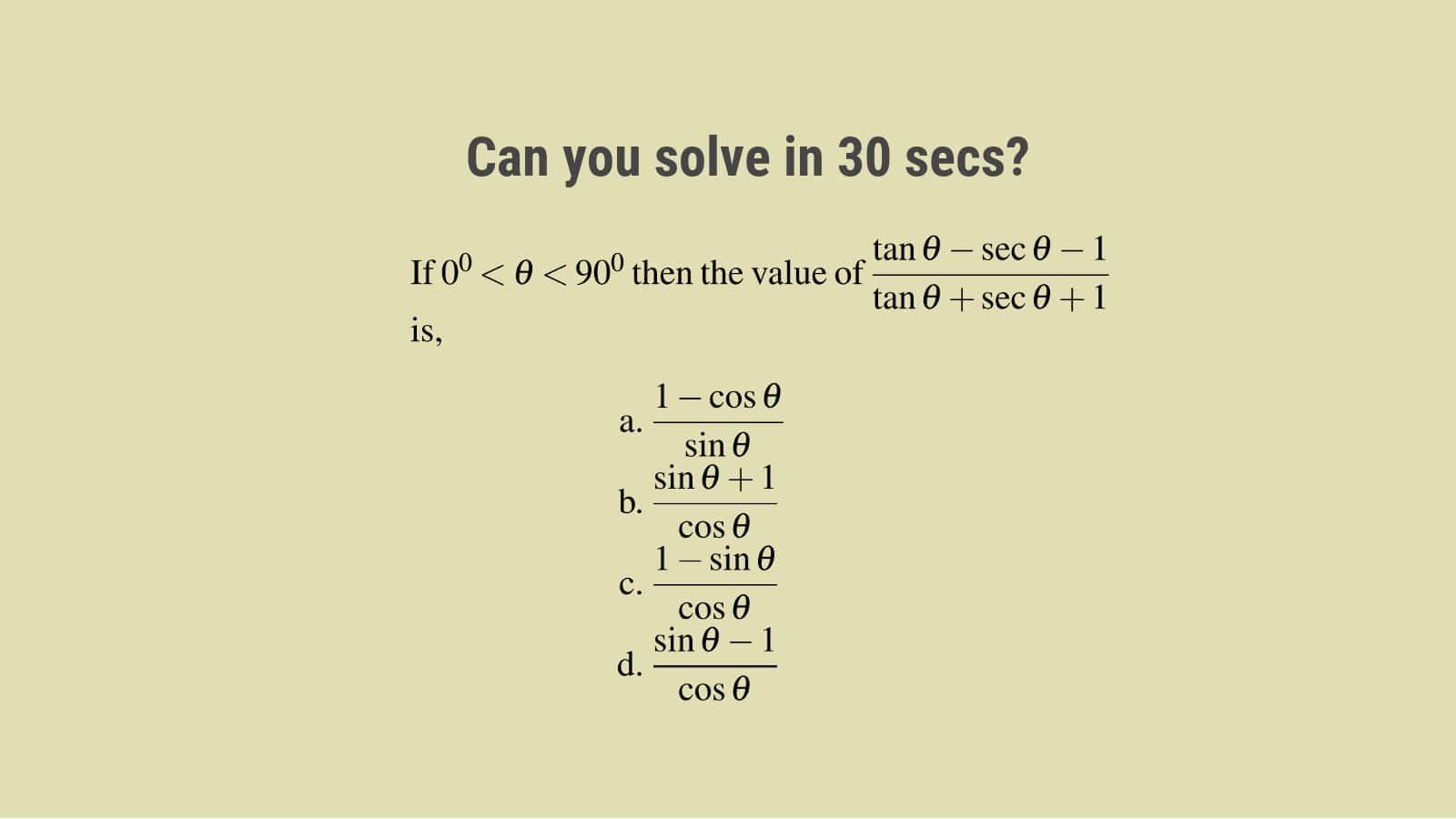
Trigonometry for SSC CGL Question Set 40 with Answers

Trigonometry for SSC CGL Question Set 77: Solve 10 difficult trigonometry questions in 12 mins. Verify from answers. Learn to solve quick from solutions.

Answer to the questions and link to the quick solutions are at the end.

---

10 selected questions on Trigonometry for SSC CGL Set 77 - testing time 12 mins

Problem 1.

If $7\sin^2 \theta+3\cos^2 \theta=4$, then the value of $\tan \theta$, where $\theta$ is acute, is,

1. $1$
2. $\displaystyle\frac{1}{\sqrt{3}}$
3. $\sqrt{3}$
4. $\displaystyle\frac{1}{\sqrt{2}}$

Problem 2.

If $\alpha + \beta=90^0$, then the expression $\displaystyle\frac{\tan \alpha}{\tan \beta}+ \sin^2 \alpha + \sin^2 \beta$ is equal to,

1. $\sec^2 \beta$
2. $\sec^2 \alpha$
3. $\tan^2 \beta$
4. $\tan^2 \alpha$

Problem 3.

If $0^0 \lt \theta \lt 90^0$ then the value of $\displaystyle\frac{\tan \theta-\sec \theta-1}{\tan \theta + \sec \theta +1}$ is,

1. $\displaystyle\frac{1-\cos \theta}{\sin \theta}$
2. $\displaystyle\frac{\sin \theta +1}{\cos \theta}$
3. $\displaystyle\frac{1-\sin \theta}{\cos \theta}$
4. $\displaystyle\frac{\sin \theta-1}{\cos \theta}$

Problem 4.

If $5\sin \theta=3$, then the numerical value of $\displaystyle\frac{\sec \theta - \tan \theta}{\sec \theta + \tan \theta}$ is,

1. $\displaystyle\frac{1}{2}$
2. $\displaystyle\frac{1}{4}$
3. $\displaystyle\frac{1}{3}$
4. $\displaystyle\frac{1}{5}$

Problem 5.

If $\displaystyle\frac{\sec \theta + \tan \theta}{\sec \theta - \tan \theta}=2\displaystyle\frac{51}{79}$, the value of $\sin \theta$ is,

1. $\displaystyle\frac{39}{72}$
2. $\displaystyle\frac{91}{144}$
3. $\displaystyle\frac{65}{144}$
4. $\displaystyle\frac{35}{72}$

Problem 6.

The value of $\theta$ ($0 \leq \theta \leq 90^0$) satisfying $2\sin^2 \theta=3\cos \theta$ is,

1. $60^0$
2. $45^0$
3. $90^0$
4. $30^0$

Problem 7.

If $a$, $b$, $c$ are the lengths of three sides of a $\triangle ABC$. If $a$, $b$ and $c$ are related by the relation, $a^2+b^2+c^2=ab+bc+ca$, then the value of $\sin^2 \text{A}+\sin^2 \text{B}+\sin^2 \text{C}$ is,

1. $\displaystyle\frac{3}{4}$
2. $\displaystyle\frac{9}{4}$
3. $\displaystyle\frac{3}{2}$
4. $\displaystyle\frac{3\sqrt{3}}{2}$

Problem 8.

If $x\cos^2 30^0.\sin 60^0=\displaystyle\frac{\tan^2 45^0.\sec 60^0}{\text{cosec } 60^0}$, then the value of $x$ is,

1. $\displaystyle\frac{1}{\sqrt{3}}$
2. $\displaystyle\frac{1}{2}$
3. $2\displaystyle\frac{2}{3}$
4. $\displaystyle\frac{1}{\sqrt{2}}$

Problem 9.

If $\sec \theta-\cos \theta = \displaystyle\frac{3}{2}$, where $\theta$ is a positive acute angle, the value of $\sec \theta$ is,

1. $2$
2. $0$
3. $-\displaystyle\frac{1}{2}$
4. $1$

Problem 10.

If $1+\cos^2 \theta=3\sin \theta.\cos \theta$, then the integral value of $\text{cot } \theta$ $\left(0 \lt \theta \lt \displaystyle\frac{\pi}{2}\right)$ is equal to,

1. $0$
2. $3$
3. $1$
4. $2$

Know how to solve these 10 questions quickly from the paired solution set at,

SSC CGL level Solution Set 77 on Trigonometry 7.

---

Answers to the questions on trigonometry for SSC CGL Set 77

Problem 1. Answer: Option b: $\displaystyle\frac{1}{\sqrt{3}}$.

Problem 2. Answer: Option b: $\sec^2 \alpha$.

Problem 3. Answer: Option d: $\displaystyle\frac{\sin \theta-1}{\cos \theta}$.

Problem 4. Answer: Option b: $\displaystyle\frac{1}{4}$.

Problem 5. Answer: Option c: $\displaystyle\frac{65}{144}$.

Problem 6. Answer: Option a: $60^0$.

Problem 7. Answer: Option b: $\displaystyle\frac{9}{4}$.

Problem 8. Answer: Option c: $2\displaystyle\frac{2}{3}$.

Problem 9. Answer: Option a: $2$.

Problem 10. Answer: Option c: $1$.

---

Guided help on Trigonometry in Suresolv

To get the best results out of the extensive range of articles of tutorials, questions and solutions on Trigonometry in Suresolv, follow the guide,

Reading and Practice Guide on Trigonometry in Suresolv for SSC CHSL, SSC CGL, SSC CGL Tier II Other Competitive exams.

The guide list of articles is up-to-date.

---